Question and Answers Forum

IntegrationQuestion and Answers: Page 130

Question Number 121875 Answers: 2 Comments: 0

Question Number 121862 Answers: 1 Comments: 0

1)explicite f(a)=∫_0 ^∞ ((t^(a−1) lnt)/(1+t))dt with 0<a<1 2)calculate ∫_0 ^∞ ((lnt)/((1+t)(√t)))dt

$$\left.\mathrm{1}\right){explicite}\:{f}\left({a}\right)=\int_{\mathrm{0}} ^{\infty} \frac{{t}^{{a}−\mathrm{1}} {lnt}}{\mathrm{1}+{t}}{dt} \\ $$$${with}\:\mathrm{0}<{a}<\mathrm{1} \\ $$$$\left.\mathrm{2}\right){calculate}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{lnt}}{\left(\mathrm{1}+{t}\right)\sqrt{{t}}}{dt} \\ $$

Question Number 121860 Answers: 0 Comments: 0

calculate ∫∫_([0,1]^2 ) ((arctan((√(x^2 +y^2 ))))/(x^2 +y^2 ))dxdy

$${calculate}\:\int\int_{\left[\mathrm{0},\mathrm{1}\right]^{\mathrm{2}} } \:\:\:\frac{{arctan}\left(\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\right)}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }{dxdy} \\ $$

Question Number 121859 Answers: 2 Comments: 0

find ∫ (dx/((x−1)(√(x+1))−(x+1)(√(x−1))))

$${find}\:\int\:\:\:\frac{{dx}}{\left({x}−\mathrm{1}\right)\sqrt{{x}+\mathrm{1}}−\left({x}+\mathrm{1}\right)\sqrt{{x}−\mathrm{1}}} \\ $$

Question Number 121858 Answers: 0 Comments: 0

decompose F(x) =(x^n /(x^(2n+1) +1)) 2)find the value of ∫_0 ^∞ (x^n /(x^(2n+1) +1))dx n integr natural

$${decompose}\:{F}\left({x}\right)\:=\frac{{x}^{{n}} }{{x}^{\mathrm{2}{n}+\mathrm{1}} +\mathrm{1}} \\ $$$$\left.\mathrm{2}\right){find}\:{the}\:{value}\:{of}\:\int_{\mathrm{0}} ^{\infty} \:\frac{{x}^{{n}} }{{x}^{\mathrm{2}{n}+\mathrm{1}} +\mathrm{1}}{dx} \\ $$$${n}\:{integr}\:{natural} \\ $$

Question Number 121857 Answers: 0 Comments: 0

find ∫_0 ^∞ xe^(−x^2 ) arctan(2x)dx

$${find}\:\int_{\mathrm{0}} ^{\infty} \:{xe}^{−{x}^{\mathrm{2}} } {arctan}\left(\mathrm{2}{x}\right){dx} \\ $$

Question Number 121908 Answers: 0 Comments: 0

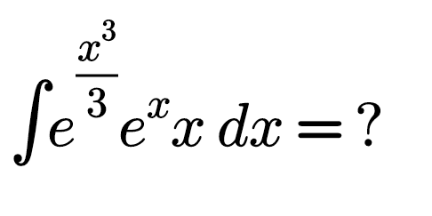
Question Number 121854 Answers: 0 Comments: 0

Question Number 121825 Answers: 1 Comments: 1

∫ (dx/(x−4(√x))) ?

$$\:\:\int\:\frac{{dx}}{{x}−\mathrm{4}\sqrt{{x}}}\:? \\ $$

Question Number 121814 Answers: 0 Comments: 0

Question Number 121774 Answers: 0 Comments: 0

... advanced calculus... evaluate: Σ_(n=1) ^∞ (((H_n )^2 )/n^2 ) =? where H_n =Σ_(k=1) ^n (1/k) (harmonic number)

$$\:\:\:\:\:\:\:\:\:\:...\:{advanced}\:\:{calculus}... \\ $$$$\:\:\:\:\:\:\:{evaluate}: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left({H}_{{n}} \right)^{\mathrm{2}} }{{n}^{\mathrm{2}} }\:=? \\ $$$$\:\:\:\:{where}\:\:\:{H}_{{n}} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{k}}\:\left({harmonic}\:{number}\right) \\ $$

Question Number 121766 Answers: 0 Comments: 0

The tangent line to y = f(x) at (3,4) is given y=3x−5. What is the tangent line to y = f^(−1) (x) at (3,4) where f(x) is an injective continous function that satisfies f(3)=4.

$$\mathrm{The}\:\mathrm{tangent}\:\mathrm{line}\:\mathrm{to}\:\mathrm{y}\:=\:\mathrm{f}\left(\mathrm{x}\right)\:\mathrm{at}\:\left(\mathrm{3},\mathrm{4}\right)\:\mathrm{is} \\ $$$$\mathrm{given}\:\mathrm{y}=\mathrm{3x}−\mathrm{5}.\:\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\mathrm{tangent}\:\mathrm{line} \\ $$$$\mathrm{to}\:\mathrm{y}\:=\:\mathrm{f}^{−\mathrm{1}} \left(\mathrm{x}\right)\:\mathrm{at}\:\left(\mathrm{3},\mathrm{4}\right)\:\mathrm{where}\:\mathrm{f}\left(\mathrm{x}\right)\:\mathrm{is}\:\mathrm{an} \\ $$$$\mathrm{injective}\:\mathrm{continous}\:\mathrm{function}\:\mathrm{that}\:\mathrm{satisfies} \\ $$$$\mathrm{f}\left(\mathrm{3}\right)=\mathrm{4}. \\ $$

Question Number 121712 Answers: 1 Comments: 0

Question Number 121707 Answers: 1 Comments: 0

Question Number 121704 Answers: 1 Comments: 0

Question Number 121696 Answers: 2 Comments: 0

∫ ((x^4 −5x^3 +6x^2 −18)/(x^3 −3x^2 )) dx ?

$$\:\:\int\:\frac{{x}^{\mathrm{4}} −\mathrm{5}{x}^{\mathrm{3}} +\mathrm{6}{x}^{\mathrm{2}} −\mathrm{18}}{{x}^{\mathrm{3}} −\mathrm{3}{x}^{\mathrm{2}} }\:{dx}\:? \\ $$

Question Number 121680 Answers: 1 Comments: 0

please evaluate ∫x^x dx

$${please}\:{evaluate}\:\int{x}^{{x}} {dx} \\ $$

Question Number 121674 Answers: 3 Comments: 0

... advanced calculus... prove that : Ω =∫_0 ^( ∞) ((sin^4 (x)ln(x))/x^2 )dx=(π/4)(1−γ) γ:euler−mascheroni constant m.n.july.1970

$$\:\:\:\:\:\:\:\:\:...\:\:{advanced}\:\:{calculus}... \\ $$$$\:\:\:\:{prove}\:{that}\:: \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\Omega\:=\int_{\mathrm{0}} ^{\:\infty} \frac{{sin}^{\mathrm{4}} \left({x}\right){ln}\left({x}\right)}{{x}^{\mathrm{2}} }{dx}=\frac{\pi}{\mathrm{4}}\left(\mathrm{1}−\gamma\right) \\ $$$$\gamma:{euler}−{mascheroni}\:{constant} \\ $$$$\:\:\:\:\:\:{m}.{n}.{july}.\mathrm{1970} \\ $$

Question Number 121611 Answers: 1 Comments: 2

∫_0 ^2 sin (2πx)cos (5πx) dx ?

$$\:\underset{\mathrm{0}} {\overset{\mathrm{2}} {\int}}\:\mathrm{sin}\:\left(\mathrm{2}\pi\mathrm{x}\right)\mathrm{cos}\:\left(\mathrm{5}\pi\mathrm{x}\right)\:\mathrm{dx}\:?\: \\ $$

Question Number 121602 Answers: 2 Comments: 0

Question Number 121601 Answers: 4 Comments: 0

∫ (dx/(x (√(3+x^2 )))) ?

$$\:\:\int\:\frac{\mathrm{dx}}{\mathrm{x}\:\sqrt{\mathrm{3}+\mathrm{x}^{\mathrm{2}} }}\:? \\ $$

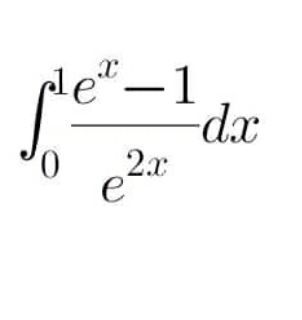
Question Number 121548 Answers: 1 Comments: 0

∫_0 ^(π/4) tan^6 x sec x dx =?

$$\:\underset{\mathrm{0}} {\overset{\pi/\mathrm{4}} {\int}}\:\mathrm{tan}\:^{\mathrm{6}} \mathrm{x}\:\mathrm{sec}\:\mathrm{x}\:\mathrm{dx}\:=? \\ $$

Question Number 121519 Answers: 1 Comments: 0

∫ ((1−x^4 )/(x^2 (√(x^4 +x^2 +1)))) dx ?

$$\:\:\int\:\frac{\mathrm{1}−\mathrm{x}^{\mathrm{4}} }{\mathrm{x}^{\mathrm{2}} \:\sqrt{\mathrm{x}^{\mathrm{4}} +\mathrm{x}^{\mathrm{2}} +\mathrm{1}}}\:\mathrm{dx}\:? \\ $$

Question Number 121498 Answers: 1 Comments: 0

Evaluate Σ_(n=1) ^∞ ((sin(n))/n)

$$ \\ $$$$\mathrm{Evaluate} \\ $$$$\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{sin}\left(\mathrm{n}\right)}{\mathrm{n}} \\ $$

Question Number 121500 Answers: 3 Comments: 1

(1) ∫ (dx/(x^4 +2x^2 +9)) ? (2) arc tan ((x/3))−arc tan ((x/3))= arc tan ((1/5))

$$\:\left(\mathrm{1}\right)\:\int\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{4}} +\mathrm{2x}^{\mathrm{2}} +\mathrm{9}}\:? \\ $$$$\left(\mathrm{2}\right)\:\mathrm{arc}\:\mathrm{tan}\:\left(\frac{\mathrm{x}}{\mathrm{3}}\right)−\mathrm{arc}\:\mathrm{tan}\:\left(\frac{\mathrm{x}}{\mathrm{3}}\right)=\:\mathrm{arc}\:\mathrm{tan}\:\left(\frac{\mathrm{1}}{\mathrm{5}}\right) \\ $$

Question Number 121492 Answers: 3 Comments: 0

calculate ∫_0 ^(+∞) (dx/((x^4 +1)^3 ))

$$\mathrm{calculate}\:\int_{\mathrm{0}} ^{+\infty} \:\:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{4}} +\mathrm{1}\right)^{\mathrm{3}} } \\ $$

Pg 125 Pg 126 Pg 127 Pg 128 Pg 129 Pg 130 Pg 131 Pg 132 Pg 133 Pg 134

Contact: info@tinkutara.com