
IntegrationQuestion and Answers: Page 129
Question Number 123896 Answers: 1 Comments: 0
Question Number 123920 Answers: 2 Comments: 0
Question Number 123866 Answers: 2 Comments: 0
Question Number 123859 Answers: 1 Comments: 0
Question Number 123793 Answers: 2 Comments: 0
Question Number 123769 Answers: 0 Comments: 1

Question Number 123768 Answers: 0 Comments: 0

Question Number 123767 Answers: 1 Comments: 0

Question Number 123764 Answers: 1 Comments: 0
Question Number 123745 Answers: 0 Comments: 0
Question Number 123710 Answers: 2 Comments: 0
Question Number 123703 Answers: 1 Comments: 0
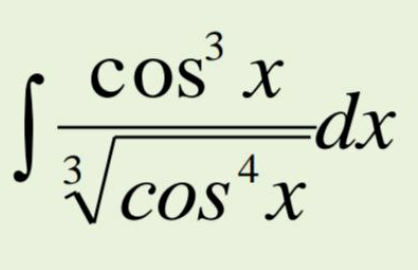
Question Number 123676 Answers: 2 Comments: 0
Question Number 123674 Answers: 2 Comments: 0
Question Number 123673 Answers: 0 Comments: 0
Question Number 123687 Answers: 1 Comments: 0
Question Number 123639 Answers: 1 Comments: 0
Question Number 123552 Answers: 4 Comments: 0
Question Number 123550 Answers: 3 Comments: 0
Question Number 123513 Answers: 3 Comments: 1
Question Number 123495 Answers: 1 Comments: 0
Question Number 123494 Answers: 2 Comments: 0
Question Number 123462 Answers: 1 Comments: 0
Question Number 123456 Answers: 0 Comments: 0
Question Number 123452 Answers: 4 Comments: 1
$$\int\frac{{dx}}{\:\left({x}^{\mathrm{2}} +{n}\right)\sqrt{{x}^{\mathrm{2}} +{a}}} \\ $$
Question Number 123454 Answers: 1 Comments: 0
Pg 124 Pg 125 Pg 126 Pg 127 Pg 128 Pg 129 Pg 130 Pg 131 Pg 132 Pg 133
