Question and Answers Forum

IntegrationQuestion and Answers: Page 120

Question Number 127948 Answers: 1 Comments: 0

Question Number 127952 Answers: 1 Comments: 0

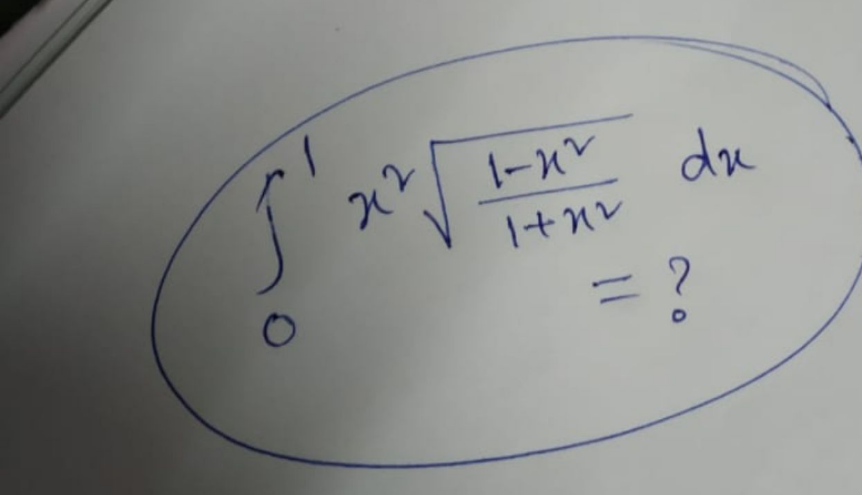
Question Number 127925 Answers: 1 Comments: 0

find F(a)=∫_0 ^1 (√((1+a^2 t^2 )/(1−t^2 ))) dt for background see Q127811.

$${find}\:{F}\left({a}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\frac{\mathrm{1}+{a}^{\mathrm{2}} {t}^{\mathrm{2}} }{\mathrm{1}−{t}^{\mathrm{2}} }}\:{dt} \\ $$$$ \\ $$$${for}\:{background}\:{see}\:{Q}\mathrm{127811}. \\ $$

Question Number 127904 Answers: 2 Comments: 0

prove that ∫_0 ^( 100) (dx/( (√(x(100−x))))) = π

$$\:\mathrm{prove}\:\mathrm{that}\:\int_{\mathrm{0}} ^{\:\mathrm{100}} \:\frac{\mathrm{dx}}{\:\sqrt{\mathrm{x}\left(\mathrm{100}−\mathrm{x}\right)}}\:=\:\pi \\ $$

Question Number 127885 Answers: 1 Comments: 0

∫(((sin (2tan^(−1) (x)+x))/x)) the limit [0,∞)

$$\int\left(\frac{\mathrm{sin}\:\left(\mathrm{2tan}^{−\mathrm{1}} \left({x}\right)+{x}\right)}{{x}}\right)\:\:{the}\:{limit}\:\left[\mathrm{0},\infty\right) \\ $$

Question Number 127870 Answers: 2 Comments: 0

2021 HAPPY NEW Year 1)∫((x^3 +3x+2)/((x^2 +1)^2 (x+1)))dx 2)∫((2cos(x)−sin(x))/(3sin(x)+5cos(x)))dx 3)∫((tan(2x))/( (√(sin^6 (x)+cos^6 (x)))))dx 4)∫x(√((1−x^2 )/(1+x^2 ))) dx

$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2021} \\ $$$${HAPPY}\:{NEW}\:{Year} \\ $$$$\left.\mathrm{1}\right)\int\frac{{x}^{\mathrm{3}} +\mathrm{3}{x}+\mathrm{2}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} \left({x}+\mathrm{1}\right)}{dx} \\ $$$$ \\ $$$$\left.\mathrm{2}\right)\int\frac{\mathrm{2}{cos}\left({x}\right)−{sin}\left({x}\right)}{\mathrm{3}{sin}\left({x}\right)+\mathrm{5}{cos}\left({x}\right)}{dx} \\ $$$$ \\ $$$$\left.\mathrm{3}\right)\int\frac{{tan}\left(\mathrm{2}{x}\right)}{\:\sqrt{{sin}^{\mathrm{6}} \left({x}\right)+{cos}^{\mathrm{6}} \left({x}\right)}}{dx} \\ $$$$ \\ $$$$\left.\mathrm{4}\right)\int{x}\sqrt{\frac{\mathrm{1}−{x}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} }}\:{dx} \\ $$

Question Number 127857 Answers: 0 Comments: 1

∫(√x)e^x dx ?

$$\int\sqrt{{x}}{e}^{{x}} {dx}\:\:? \\ $$

Question Number 127851 Answers: 1 Comments: 0

ψ = ∫ (dx/(x^3 (((x^5 +1)^3 ))^(1/5) )) ?

$$\:\psi\:=\:\int\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{3}} \:\sqrt[{\mathrm{5}}]{\left(\mathrm{x}^{\mathrm{5}} +\mathrm{1}\right)^{\mathrm{3}} }}\:?\: \\ $$

Question Number 127833 Answers: 2 Comments: 0

Question Number 127815 Answers: 0 Comments: 1

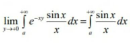
Question Number 127789 Answers: 0 Comments: 8

Question Number 127779 Answers: 2 Comments: 0

find A_n = ∫_0 ^(+∞) (dx/((x^2 +1)^n ))

$${find}\:{A}_{{n}} =\:\int_{\mathrm{0}} ^{+\infty} \frac{{dx}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{{n}} } \\ $$

Question Number 127777 Answers: 1 Comments: 0

explicite f(a)=∫_0 ^∞ ((lnx)/(x^2 −x+a))dx with a>(1/4)

$${explicite}\:{f}\left({a}\right)=\int_{\mathrm{0}} ^{\infty} \:\frac{{lnx}}{{x}^{\mathrm{2}} −{x}+{a}}{dx} \\ $$$${with}\:\:\:{a}>\frac{\mathrm{1}}{\mathrm{4}} \\ $$

Question Number 127776 Answers: 0 Comments: 0

calculate ∫_0 ^∞ ((lnx)/((x^2 −x+1)^2 ))dx

$${calculate}\:\int_{\mathrm{0}} ^{\infty} \:\frac{{lnx}}{\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)^{\mathrm{2}} }{dx} \\ $$

Question Number 127775 Answers: 1 Comments: 0

prove that ∫_0 ^∞ e^(−x) lnxdx=−γ

$${prove}\:{that}\:\int_{\mathrm{0}} ^{\infty} \:{e}^{−{x}} {lnxdx}=−\gamma \\ $$

Question Number 127774 Answers: 2 Comments: 0

calculate u_n =∫_0 ^1 x^n (√(1−x^4 ))dx

$${calculate}\:\:{u}_{{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}^{{n}} \sqrt{\mathrm{1}−{x}^{\mathrm{4}} }{dx} \\ $$

Question Number 127772 Answers: 1 Comments: 0

calculate ∫_0 ^(2π) (dx/((cosx +2sinx)^2 ))

$${calculate}\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:\frac{{dx}}{\left({cosx}\:+\mathrm{2}{sinx}\right)^{\mathrm{2}} } \\ $$

Question Number 127732 Answers: 0 Comments: 0

z=x+iy why ((f(z))/(z−a)) not analytical? / not analytical at z=a?

$${z}={x}+{iy} \\ $$$${why}\:\frac{{f}\left({z}\right)}{{z}−{a}}\:{not}\:{analytical}?\:/\:{not}\:{analytical}\:{at}\:{z}={a}? \\ $$$$ \\ $$

Question Number 127704 Answers: 1 Comments: 0

if f(x)= { ((x−n ; 2n ≤ x ≤2n+1)),((n+1 ; 2n+1≤x≤2n+2 )) :} where n =0,1,2,3,..,9 find ∫_0 ^(20) f(x)dx

$$ \\ $$$${if}\:{f}\left({x}\right)=\begin{cases}{{x}−{n}\:;\:\mathrm{2}{n}\:\leqslant\:{x}\:\leqslant\mathrm{2}{n}+\mathrm{1}}\\{{n}+\mathrm{1}\:;\:\mathrm{2}{n}+\mathrm{1}\leqslant{x}\leqslant\mathrm{2}{n}+\mathrm{2}\:}\end{cases}\:{where}\:\:{n}\:=\mathrm{0},\mathrm{1},\mathrm{2},\mathrm{3},..,\mathrm{9} \\ $$$${find}\:\int_{\mathrm{0}} ^{\mathrm{20}} {f}\left({x}\right){dx} \\ $$

Question Number 127679 Answers: 0 Comments: 0

its 9:30pm in Cameroon

$${its}\:\mathrm{9}:\mathrm{30}{pm}\:{in}\:{Cameroon} \\ $$

Question Number 127631 Answers: 0 Comments: 0

Let f∈C^∞ (R,R) , ∀ n∈N M_n =∣∣f^((n)) ∣∣_∞ and u_n =((2^(n−1) M_n )/M_(n−1) ) for n≥1 Show that if M_1 <(√(2M_0 M_2 )) then u_n <u_(n+1) for n≥1

$${Let}\:{f}\in{C}^{\infty} \left(\mathbb{R},\mathbb{R}\right)\:,\:\forall\:{n}\in\mathbb{N}\:\:\:{M}_{{n}} =\mid\mid{f}^{\left({n}\right)} \mid\mid_{\infty} \:\: \\ $$$${and}\:\:{u}_{{n}} =\frac{\mathrm{2}^{{n}−\mathrm{1}} {M}_{{n}} }{{M}_{{n}−\mathrm{1}} }\:\:\:{for}\:{n}\geqslant\mathrm{1}\: \\ $$$${Show}\:{that}\:{if}\:\:\:{M}_{\mathrm{1}} <\sqrt{\mathrm{2}{M}_{\mathrm{0}} {M}_{\mathrm{2}} }\:{then}\:{u}_{{n}} <{u}_{{n}+\mathrm{1}} \:{for}\:{n}\geqslant\mathrm{1} \\ $$

Question Number 127618 Answers: 2 Comments: 0

∫ (dx/(x^(2021) (1+x^(2020) ))) ?

$$\:\int\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2021}} \left(\mathrm{1}+\mathrm{x}^{\mathrm{2020}} \right)}\:?\: \\ $$

Question Number 127616 Answers: 0 Comments: 1

If ∫_1 ^( 4) f(x) dx = 6 , then ∫_1 ^( 4) f(5−x) dx ?

$$\:\mathrm{If}\:\int_{\mathrm{1}} ^{\:\mathrm{4}} \mathrm{f}\left(\mathrm{x}\right)\:\mathrm{dx}\:=\:\mathrm{6}\:,\:\mathrm{then}\:\int_{\mathrm{1}} ^{\:\mathrm{4}} \mathrm{f}\left(\mathrm{5}−\mathrm{x}\right)\:\mathrm{dx}\:?\: \\ $$

Question Number 127605 Answers: 1 Comments: 0

find arg(z) where z=1+cosα+icosβ

$${find}\:{arg}\left({z}\right) \\ $$$${where}\:\boldsymbol{{z}}=\mathrm{1}+\boldsymbol{{cos}}\alpha+{icos}\beta \\ $$

Question Number 127604 Answers: 2 Comments: 0

Question Number 127587 Answers: 1 Comments: 0

Pg 115 Pg 116 Pg 117 Pg 118 Pg 119 Pg 120 Pg 121 Pg 122 Pg 123 Pg 124

Contact: info@tinkutara.com