Question and Answers Forum

IntegrationQuestion and Answers: Page 100

Question Number 136922 Answers: 1 Comments: 0

∫ ln∣tan^(−1) x∣ dx = ?

$$\int\:{ln}\mid{tan}^{−\mathrm{1}} {x}\mid\:{dx}\:=\:? \\ $$

Question Number 136921 Answers: 1 Comments: 0

evaluation of :: 𝛗=∫_0 ^( 1) ((xln(1+x))/(1+x^2 ))dx solution: 𝛗=^(I.B.P ) [(1/2)ln(1+x^2 )ln(1+x)]_0 ^1 −(1/2){∫_0 ^( 1) ((ln(1+x^2 ))/(1+x))dx=𝚽} 𝛗=(1/2)ln^2 (2)−(1/2) 𝚽 ........✓ 𝚽=∫_0 ^( 1) ((ln(1+x^2 ))/(1+x))dx =??? h(a)=∫_0 ^( 1) ((ln(1+ax^2 ))/(1+x))dx h′(a)=∫_0 ^( 1) (∂/∂_a )(((ln(1+ax^2 ))/(1+x)))dx h′(a)=∫_0 ^( 1) (x^2 /((1+x)(1+ax^2 )))dx h′(a)=(1/(1+a))∫_0 ^( 1) (1/(1+x))dx+(1/(1+a))∫_0 ^( 1) (x/(1+ax^2 ))dx−(1/(1+a))∫_0 ^( 1) (1/(1+ax^2 ))dx =(1/(1+a))ln(2)+(1/2).(1/(a(1+a)))ln(1+a)−((√a)/(a(1+a)))[(tan^(−1) (x(√a) )]_0 ^1 =((ln(2))/(1+a))+(1/2).(1/(a(1+a))) ln(1+a)−((√a)/(a(1+a)))tan^(−1) ((√a) ) ∫_0 ^( 1) h′(a)da=ln^2 (2)+(1/2)∫_0 ^( 1) ((ln(1+a))/a)da−(1/4)ln^2 (2)−((π^2 /(16))) =ln^2 (2)+(π^2 /(24))−(1/4)ln^2 (2)−(π^2 /(16)) =(3/4)ln^2 (2)−(π^2 /(48)) ∴ h(1)=𝚽=(3/4)ln^2 (2)−(π^2 /(48)) ..✓ 𝛗=(1/2)ln^2 (2)−(3/8)ln^2 (2)+(π^2 /(96)) 𝛗=(1/8)ln^2 (2)+(π^2 /(96))

Question Number 136906 Answers: 2 Comments: 0

∫_9 ^∞ (1/((x−8)^(3/2) ))dx

$$\underset{\mathrm{9}} {\overset{\infty} {\int}}\frac{\mathrm{1}}{\left({x}−\mathrm{8}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }{dx} \\ $$

Question Number 136905 Answers: 1 Comments: 0

∫_0 ^3 ((56)/(x^2 −6x+5))dx

$$\underset{\mathrm{0}} {\overset{\mathrm{3}} {\int}}\frac{\mathrm{56}}{{x}^{\mathrm{2}} −\mathrm{6}{x}+\mathrm{5}}{dx} \\ $$

Question Number 136929 Answers: 2 Comments: 0

∫ (e^(ln (sin^(−1) x)) /( (√(1−x^2 )))) dx = ?

$$\int\:\frac{\mathrm{e}^{\mathrm{ln}\:\left(\mathrm{sin}^{−\mathrm{1}} \mathrm{x}\right)} }{\:\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }}\:\mathrm{dx}\:=\:?\: \\ $$

Question Number 136883 Answers: 2 Comments: 0

Given log _5 (7^a −2)= log _7 (5^a +2) . Find the value ∫_a ^e ((1+ln (x))/(x^x +x^(−x) )) dx .

$$\mathrm{Given}\:\mathrm{log}\:_{\mathrm{5}} \left(\mathrm{7}^{{a}} −\mathrm{2}\right)=\:\mathrm{log}\:_{\mathrm{7}} \left(\mathrm{5}^{{a}} +\mathrm{2}\right) \\ $$$$.\:\mathrm{Find}\:\mathrm{the}\:\mathrm{value}\:\int_{{a}} ^{\mathrm{e}} \:\frac{\mathrm{1}+\mathrm{ln}\:\left(\mathrm{x}\right)}{\mathrm{x}^{\mathrm{x}} +\mathrm{x}^{−\mathrm{x}} }\:\mathrm{dx}\:. \\ $$

Question Number 136868 Answers: 1 Comments: 0

...... nice calculus.... prove that :: i: ∫_(−∞) ^( ∞) (dx/((1+x+e^x )^2 +π^2 )) =(2/3) ii: ∫_0 ^( ∞) ((sin(tan(x)))/x)dx=(π/2)(1−(1/e))

$$\:\:\:\:\:\:\:\:\:......\:{nice}\:\:\:\:\:{calculus}.... \\ $$$$\:\:{prove}\:\:{that}\::: \\ $$$$\:{i}:\:\:\int_{−\infty} ^{\:\infty} \frac{{dx}}{\left(\mathrm{1}+{x}+{e}^{{x}} \right)^{\mathrm{2}} +\pi^{\mathrm{2}} }\:=\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\:{ii}:\:\int_{\mathrm{0}} ^{\:\infty} \frac{{sin}\left({tan}\left({x}\right)\right)}{{x}}{dx}=\frac{\pi}{\mathrm{2}}\left(\mathrm{1}−\frac{\mathrm{1}}{{e}}\right) \\ $$$$\:\:\:\:\: \\ $$

Question Number 136859 Answers: 0 Comments: 0

calculate ∫_0 ^∞ ((cos(cosx)−sin(sinx))/(x^2 +3))dx

$$\mathrm{calculate}\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{cos}\left(\mathrm{cosx}\right)−\mathrm{sin}\left(\mathrm{sinx}\right)}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{3}}\mathrm{dx} \\ $$

Question Number 136858 Answers: 1 Comments: 0

calculate ∫_0 ^∞ ((cos(sinx)−sin(cosx))/((x^2 +1)^2 ))dx

$$\mathrm{calculate}\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{cos}\left(\mathrm{sinx}\right)−\mathrm{sin}\left(\mathrm{cosx}\right)}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx} \\ $$

Question Number 136844 Answers: 0 Comments: 0

Question Number 136840 Answers: 3 Comments: 0

∫(√(x/(x−1))) dx

$$\:\int\sqrt{\frac{{x}}{{x}−\mathrm{1}}}\:{dx} \\ $$

Question Number 136841 Answers: 3 Comments: 0

∫(√(x^2 +1 )) dx = ?

$$\int\sqrt{{x}^{\mathrm{2}} +\mathrm{1}\:}\:{dx}\:=\:? \\ $$

Question Number 136835 Answers: 0 Comments: 0

.....nice calculus... for f(x)=f(x+π) : ∫_(−∞) ^( ∞) f(x).((sin^2 (x))/x^2 )dx=^(why???) ∫_0 ^( π) f(x)dx

$$\:\:\:\:\:\:\:\:.....{nice}\:\:\:\:\:{calculus}... \\ $$$$\:\:\:{for}\:\:\:\:{f}\left({x}\right)={f}\left({x}+\pi\right)\:: \\ $$$$\:\:\:\:\:\int_{−\infty} ^{\:\infty} {f}\left({x}\right).\frac{{sin}^{\mathrm{2}} \left({x}\right)}{{x}^{\mathrm{2}} }{dx}\overset{{why}???} {=}\int_{\mathrm{0}} ^{\:\pi} {f}\left({x}\right){dx} \\ $$

Question Number 136813 Answers: 1 Comments: 0

......advanced calculus(I).... if : Ω=∫_(π/4) ^( (π/2)) ((x.cos(2x).cos(x))/(sin^7 (x))) dx=((aπ)/(90)) then :: a=???

$$\:\:\:\:\: \\ $$$$\:\:\:......{advanced}\:\:\:\:{calculus}\left({I}\right).... \\ $$$$\:\:\:\:{if}\::\: \\ $$$$\:\:\Omega=\int_{\frac{\pi}{\mathrm{4}}} ^{\:\frac{\pi}{\mathrm{2}}} \frac{{x}.{cos}\left(\mathrm{2}{x}\right).{cos}\left({x}\right)}{{sin}^{\mathrm{7}} \left({x}\right)}\:{dx}=\frac{{a}\pi}{\mathrm{90}} \\ $$$$\:\:\:{then}\:\:::\:\:{a}=??? \\ $$$$\:\: \\ $$$$\:\:\:\: \\ $$

Question Number 136806 Answers: 2 Comments: 0

Question Number 136803 Answers: 1 Comments: 0

.....Advanced ◂.............▶ Calculus..... 𝛗=∫_(−∞) ^( ∞) ((sin((1/x^3 )))/x)dx=......??? solution:: 𝛗=^((1/x) =t) 2∫_0 ^( ∞) ((sin(t^3 ))/(1/t)).(dt/t^2 ) ............. =2∫_0 ^( ∞) ((sin(t^3 ))/t)dt ......... =^(t^3 =y) (2/3)∫_0 ^( ∞) ((sin(y))/y^(1/3) ).(dy/y^(2/3) )=(2/3)∫_0 ^( ∞) ((sin(y))/y) =^(⟨∫_0 ^( ∞) ((sin(r))/r)dr =(π/2)⟩) (π/3) ........... ........𝛗=∫_(−∞) ^( ∞) ((sin((1/x))^3 )/x)dx=(π/3) ........✓✓✓

$$\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:.....\mathscr{A}{dvanced}\:\:\:\:\blacktriangleleft.............\blacktriangleright\:\:\:\mathscr{C}{alculus}..... \\ $$$$\:\:\:\:\:\boldsymbol{\phi}=\int_{−\infty} ^{\:\infty} \frac{{sin}\left(\frac{\mathrm{1}}{{x}^{\mathrm{3}} }\right)}{{x}}{dx}=......??? \\ $$$$\:\:\:\:\:{solution}:: \\ $$$$\:\:\:\:\:\:\boldsymbol{\phi}\overset{\frac{\mathrm{1}}{{x}}\:={t}} {=}\:\mathrm{2}\int_{\mathrm{0}} ^{\:\infty} \frac{{sin}\left({t}^{\mathrm{3}} \right)}{\frac{\mathrm{1}}{{t}}}.\frac{{dt}}{{t}^{\mathrm{2}} }\:............. \\ $$$$\:\:\:\:\:\:\:\:\:\:=\mathrm{2}\int_{\mathrm{0}} ^{\:\infty} \frac{{sin}\left({t}^{\mathrm{3}} \right)}{{t}}{dt}\:......... \\ $$$$\:\:\:\:\:\:\:\:\:\:\overset{{t}^{\mathrm{3}} ={y}} {=}\:\frac{\mathrm{2}}{\mathrm{3}}\int_{\mathrm{0}} ^{\:\infty} \frac{{sin}\left({y}\right)}{{y}^{\frac{\mathrm{1}}{\mathrm{3}}} }.\frac{{dy}}{{y}^{\frac{\mathrm{2}}{\mathrm{3}}} }=\frac{\mathrm{2}}{\mathrm{3}}\int_{\mathrm{0}} ^{\:\infty} \frac{{sin}\left({y}\right)}{{y}} \\ $$$$\:\:\:\:\overset{\langle\int_{\mathrm{0}} ^{\:\infty} \frac{{sin}\left({r}\right)}{{r}}{dr}\:=\frac{\pi}{\mathrm{2}}\rangle} {=}\:\frac{\pi}{\mathrm{3}}\:........... \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:........\boldsymbol{\phi}=\int_{−\infty} ^{\:\infty} \frac{{sin}\left(\frac{\mathrm{1}}{{x}}\right)^{\mathrm{3}} }{{x}}{dx}=\frac{\pi}{\mathrm{3}}\:\:........\checkmark\checkmark\checkmark \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$

Question Number 136762 Answers: 0 Comments: 0

let C(a,r)={z∈C, ∣z−a∣=r } Let u,v,w ∈C(a,r) such as u+v=2w Prove that ((u−a)/(v−a)) =1 , u=v=w It shows that the middle of a segment joining two points in a circle is not in that circle

$$\:{let}\:\:{C}\left({a},{r}\right)=\left\{{z}\in\mathbb{C},\:\:\mid{z}−{a}\mid={r}\:\right\} \\ $$$${Let}\:{u},{v},{w}\:\in{C}\left({a},{r}\right)\:{such}\:{as}\:\:\:{u}+{v}=\mathrm{2}{w} \\ $$$${Prove}\:{that}\:\:\frac{{u}−{a}}{{v}−{a}}\:=\mathrm{1}\:,\:{u}={v}={w} \\ $$$$ \\ $$$${It}\:{shows}\:{that}\:{the}\:{middle}\:{of}\:{a}\:{segment}\: \\ $$$${joining}\:{two}\:{points}\:{in}\:{a}\:{circle}\:\:{is}\:{not}\:{in}\:{that}\:{circle} \\ $$

Question Number 136750 Answers: 3 Comments: 0

.....advanced calculus..... prove that :: ... 𝛗=∫_0 ^( ∞) ((1−e^(−x^2 ) )/x^2 )dx=(√π)

$$\:\:\:\:\:\:\:\:\:\:\:.....{advanced}\:\:\:\:{calculus}..... \\ $$$$\:\:\:\:\:{prove}\:\:{that}\::: \\ $$$$\:\:\:\:\:...\:\:\boldsymbol{\phi}=\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{1}−{e}^{−{x}^{\mathrm{2}} } }{{x}^{\mathrm{2}} }{dx}=\sqrt{\pi}\:\:\:\: \\ $$

Question Number 136723 Answers: 1 Comments: 0

....calculus (I)..... prove that :: f(x)= (1/( (√(1−4x)))) =^(???) Σ_(n=0) ^∞ ((( 2n)),(( n)) ) x^n

$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:....{calculus}\:\:\:\:\:\left({I}\right)..... \\ $$$$\:\:\:\:\:{prove}\:\:\:{that}\::: \\ $$$$\:\:\:\:{f}\left({x}\right)=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−\mathrm{4}{x}}}\:\overset{???} {=}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\begin{pmatrix}{\:\mathrm{2}{n}}\\{\:\:\:{n}}\end{pmatrix}\:{x}^{{n}} \\ $$$$ \\ $$

Question Number 136680 Answers: 2 Comments: 0

Question Number 136651 Answers: 2 Comments: 0

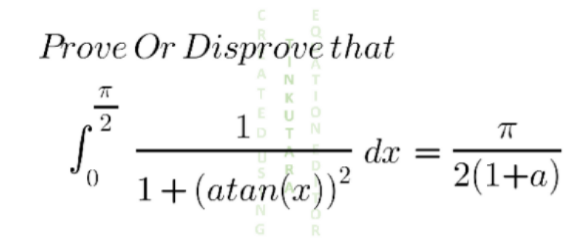
Question Number 136644 Answers: 1 Comments: 0

𝛗=∫_0 ^( 1) ((ln(x^2 +1))/x^2 )dx f(a)=∫_0 ^( 1) ((log(ax^2 +1))/x^2 )dx f ′(a)=∫_0 ^( 1) (x^2 /((ax^2 +1)x^2 ))dx=(1/a)∫_0 ^( 1) (dx/(x^2 +((1/( (√a))))^2 )) =((√a)/a)[tan^(−1) (x(√a) )]_0 ^1 =((√a)/a)tan^(−1) ((√a)) f(a)=^((√a) =u) ∫2tan^(−1) (u)du =2{u.tan^(−1) (u)−∫(u/(1+u^2 ))du}+C =2(√a) tan^(−1) ((√a) )−ln(1+a)+C f(0)=0=0+C⇒C=0 f(1)=𝛗=2((π/4))−ln(2)=(π/2)−ln(2)

$$ \\ $$$$\:\:\:\:\:\:\:\boldsymbol{\phi}=\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{ln}\left({x}^{\mathrm{2}} +\mathrm{1}\right)}{{x}^{\mathrm{2}} }{dx} \\ $$$$\:\:\:{f}\left({a}\right)=\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{log}\left({ax}^{\mathrm{2}} +\mathrm{1}\right)}{{x}^{\mathrm{2}} }{dx} \\ $$$$\:\:\:\:{f}\:'\left({a}\right)=\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{x}^{\mathrm{2}} }{\left({ax}^{\mathrm{2}} +\mathrm{1}\right){x}^{\mathrm{2}} }{dx}=\frac{\mathrm{1}}{{a}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{dx}}{{x}^{\mathrm{2}} +\left(\frac{\mathrm{1}}{\:\sqrt{{a}}}\right)^{\mathrm{2}} } \\ $$$$\:\:\:=\frac{\sqrt{{a}}}{{a}}\left[{tan}^{−\mathrm{1}} \left({x}\sqrt{{a}}\:\right)\right]_{\mathrm{0}} ^{\mathrm{1}} =\frac{\sqrt{{a}}}{{a}}{tan}^{−\mathrm{1}} \left(\sqrt{{a}}\right) \\ $$$$\:\:{f}\left({a}\right)\overset{\sqrt{{a}}\:={u}} {=}\int\mathrm{2}{tan}^{−\mathrm{1}} \left({u}\right){du} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}\left\{{u}.{tan}^{−\mathrm{1}} \:\left({u}\right)−\int\frac{{u}}{\mathrm{1}+{u}^{\mathrm{2}} }{du}\right\}+{C} \\ $$$$\:=\mathrm{2}\sqrt{{a}}\:{tan}^{−\mathrm{1}} \left(\sqrt{{a}}\:\right)−{ln}\left(\mathrm{1}+{a}\right)+{C} \\ $$$${f}\left(\mathrm{0}\right)=\mathrm{0}=\mathrm{0}+{C}\Rightarrow{C}=\mathrm{0} \\ $$$$\:\:\:{f}\left(\mathrm{1}\right)=\boldsymbol{\phi}=\mathrm{2}\left(\frac{\pi}{\mathrm{4}}\right)−{ln}\left(\mathrm{2}\right)=\frac{\pi}{\mathrm{2}}−{ln}\left(\mathrm{2}\right) \\ $$$$ \\ $$

Question Number 136626 Answers: 1 Comments: 0

..........nice calculus......... suppose that::: ϕ(p)=∫_0 ^( ∞) ((ln(1+x))/((p+x)^2 )) ...✓ find the value of:: ∫^( 1) _0 ((ϕ(p))/(1+p))dp=?...

$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:..........{nice}\:\:\:\:{calculus}......... \\ $$$$\:\:\:\:{suppose}\:{that}::: \\ $$$$\:\:\:\:\:\:\:\:\:\:\varphi\left({p}\right)=\int_{\mathrm{0}} ^{\:\infty} \frac{{ln}\left(\mathrm{1}+{x}\right)}{\left({p}+{x}\right)^{\mathrm{2}} }\:...\checkmark \\ $$$$\:\:\:\:\:\:\:\:\:\:{find}\:{the}\:{value}\:{of}:: \\ $$$$\:\:\:\:\:\:\:\underset{\mathrm{0}} {\int}^{\:\mathrm{1}} \:\frac{\varphi\left({p}\right)}{\mathrm{1}+{p}}{dp}=?... \\ $$$$\:\:\:\:\:\: \\ $$

Question Number 136572 Answers: 3 Comments: 1

....advanced calculus.... 𝛗=∫_0 ^( (π/2)) x.(tan(x))^(1/2) dx=??

$$\:\:\:\:\:\:\:\:\:\:\:\:\:....{advanced}\:\:\:\:{calculus}.... \\ $$$$\:\:\:\:\:\:\:\:\boldsymbol{\phi}=\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} {x}.\left({tan}\left({x}\right)\right)^{\frac{\mathrm{1}}{\mathrm{2}}} {dx}=?? \\ $$$$ \\ $$

Question Number 136497 Answers: 1 Comments: 2

......nice calculus..... prove:: ∫_0 ^( 1) (1/(1+ln^2 (x)))dx=∫_(0 ) ^( ∞) ((sin(x))/(1+x))dx

$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:......{nice}\:\:\:\:{calculus}..... \\ $$$$\:\:\:\:{prove}::\:\: \\ $$$$\:\:\:\:\:\:\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}+{ln}^{\mathrm{2}} \left({x}\right)}{dx}=\int_{\mathrm{0}\:} ^{\:\infty} \frac{{sin}\left({x}\right)}{\mathrm{1}+{x}}{dx} \\ $$$$ \\ $$

Question Number 136482 Answers: 0 Comments: 0

f(x)=∫_(−Π/4) ^(Π∫/4) e^(xtant) dt

$${f}\left({x}\right)=\int_{−\Pi/\mathrm{4}} ^{\Pi\int/\mathrm{4}} {e}^{{xtant}} {dt} \\ $$

Pg 95 Pg 96 Pg 97 Pg 98 Pg 99 Pg 100 Pg 101 Pg 102 Pg 103 Pg 104

Contact: info@tinkutara.com