Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 152201 by mnjuly1970 last updated on 26/Aug/21

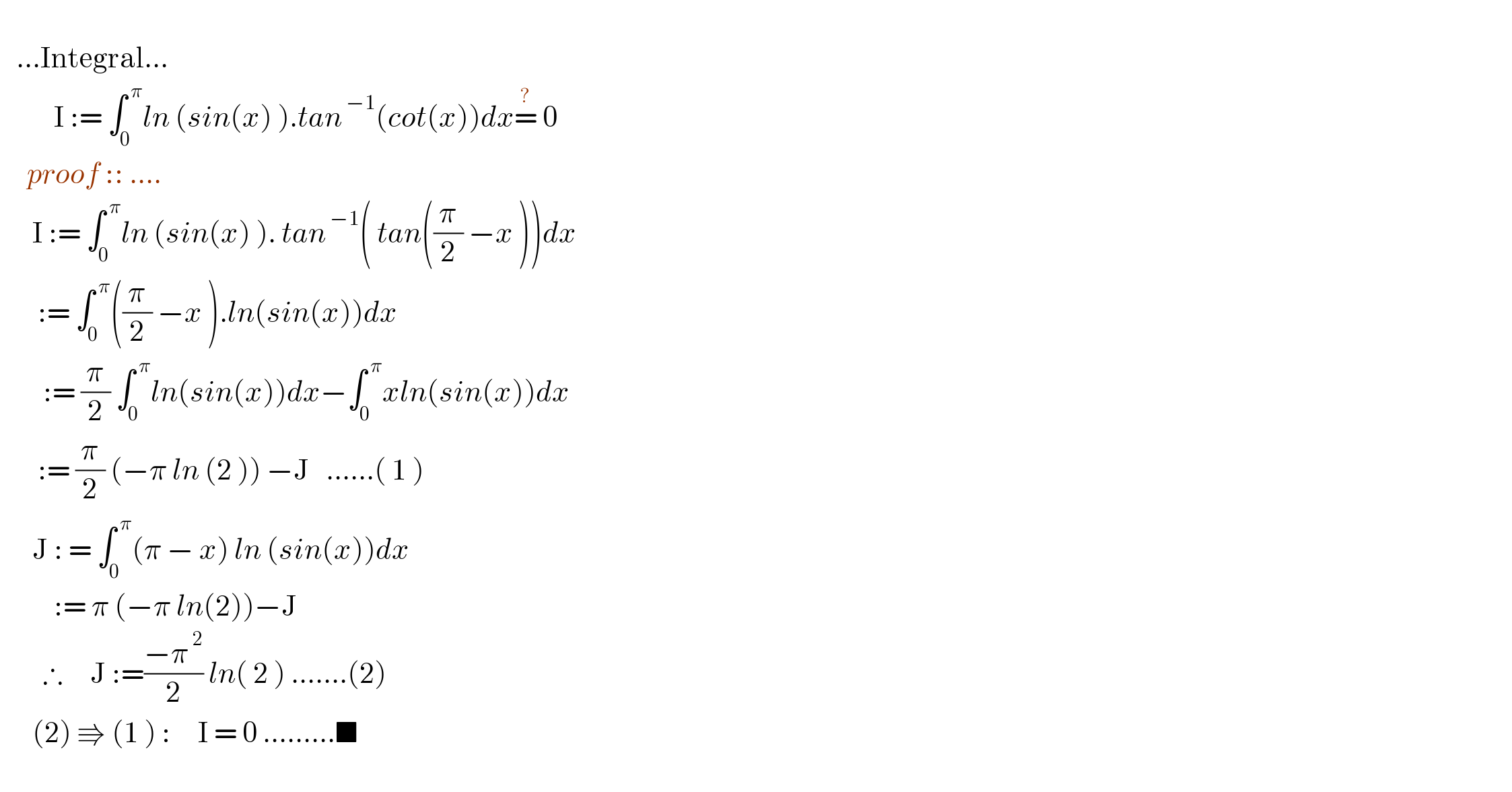
...Integral... I := ∫_0 ^( π) ln (sin(x) ).tan^( −1) (cot(x))dx=^? 0 proof :: .... I := ∫_0 ^( π) ln (sin(x) ). tan^( −1) ( tan((π/2) −x ))dx := ∫_0 ^( π) ((π/2) −x ).ln(sin(x))dx := (π/2) ∫_0 ^( π) ln(sin(x))dx−∫_0 ^( π) xln(sin(x))dx := (π/2) (−π ln (2 )) −J ......( 1 ) J : = ∫_0 ^( π) (π − x) ln (sin(x))dx := π (−π ln(2))−J ∴ J :=((−π^( 2) )/2) ln( 2 ) .......(2) (2) ⇛ (1 ) : I = 0 .........■

$$ \\ $$$$\:\:\:...\mathrm{Integral}... \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{I}\::=\:\int_{\mathrm{0}} ^{\:\pi} {ln}\:\left({sin}\left({x}\right)\:\right).{tan}^{\:−\mathrm{1}} \left({cot}\left({x}\right)\right){dx}\overset{?} {=}\:\mathrm{0} \\ $$$$\:\:\:\:\:{proof}\:::\:.... \\ $$$$\:\:\:\:\:\:\mathrm{I}\::=\:\int_{\mathrm{0}} ^{\:\pi} {ln}\:\left({sin}\left({x}\right)\:\right).\:{tan}^{\:−\mathrm{1}} \left(\:{tan}\left(\frac{\pi}{\mathrm{2}}\:−{x}\:\right)\right){dx} \\ $$$$\:\:\:\:\:\:\::=\:\int_{\mathrm{0}} ^{\:\pi} \left(\frac{\pi}{\mathrm{2}}\:−{x}\:\right).{ln}\left({sin}\left({x}\right)\right){dx} \\ $$$$\:\:\:\:\:\:\:\::=\:\frac{\pi}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\:\pi} {ln}\left({sin}\left({x}\right)\right){dx}−\int_{\mathrm{0}} ^{\:\pi} {xln}\left({sin}\left({x}\right)\right){dx} \\ $$$$\:\:\:\:\:\:\::=\:\frac{\pi}{\mathrm{2}}\:\left(−\pi\:{ln}\:\left(\mathrm{2}\:\right)\right)\:−\mathrm{J}\:\:\:......\left(\:\mathrm{1}\:\right)\:\: \\ $$$$\:\:\:\:\:\:\mathrm{J}\::\:=\:\int_{\mathrm{0}} ^{\:\pi} \left(\pi\:−\:{x}\right)\:{ln}\:\left({sin}\left({x}\right)\right){dx} \\ $$$$\:\:\:\:\:\:\:\:\:\::=\:\pi\:\left(−\pi\:{ln}\left(\mathrm{2}\right)\right)−\mathrm{J} \\ $$$$\:\:\:\:\:\:\:\:\therefore\:\:\:\:\:\mathrm{J}\::=\frac{−\pi^{\:\mathrm{2}} }{\mathrm{2}}\:{ln}\left(\:\mathrm{2}\:\right)\:.......\left(\mathrm{2}\right) \\ $$$$\:\:\:\:\:\:\left(\mathrm{2}\right)\:\Rrightarrow\:\left(\mathrm{1}\:\right)\::\:\:\:\:\:\mathrm{I}\:=\:\mathrm{0}\:.........\blacksquare \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com