
Question Number 48193 by peter frank last updated on 20/Nov/18
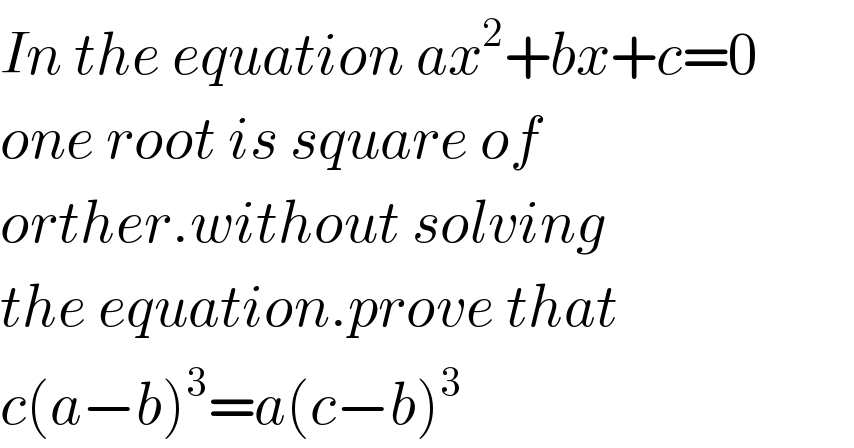
$${In}\:{the}\:{equation}\:{ax}^{\mathrm{2}} +{bx}+{c}=\mathrm{0} \\ $$$${one}\:{root}\:{is}\:{square}\:{of}\: \\ $$$${orther}.{without}\:{solving} \\ $$$${the}\:{equation}.{prove}\:{that} \\ $$$${c}\left({a}−{b}\right)^{\mathrm{3}} ={a}\left({c}−{b}\right)^{\mathrm{3}} \\ $$
Answered by MJS last updated on 20/Nov/18
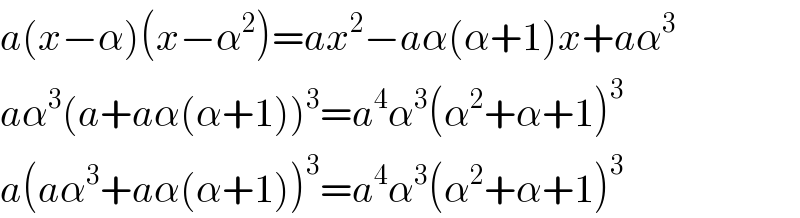
$${a}\left({x}−\alpha\right)\left({x}−\alpha^{\mathrm{2}} \right)={ax}^{\mathrm{2}} −{a}\alpha\left(\alpha+\mathrm{1}\right){x}+{a}\alpha^{\mathrm{3}} \\ $$$${a}\alpha^{\mathrm{3}} \left({a}+{a}\alpha\left(\alpha+\mathrm{1}\right)\right)^{\mathrm{3}} ={a}^{\mathrm{4}} \alpha^{\mathrm{3}} \left(\alpha^{\mathrm{2}} +\alpha+\mathrm{1}\right)^{\mathrm{3}} \\ $$$${a}\left({a}\alpha^{\mathrm{3}} +{a}\alpha\left(\alpha+\mathrm{1}\right)\right)^{\mathrm{3}} ={a}^{\mathrm{4}} \alpha^{\mathrm{3}} \left(\alpha^{\mathrm{2}} +\alpha+\mathrm{1}\right)^{\mathrm{3}} \\ $$
