
Previous in Permutation and Combination Next in Permutation and Combination
Question Number 12087 by tawa last updated on 12/Apr/17
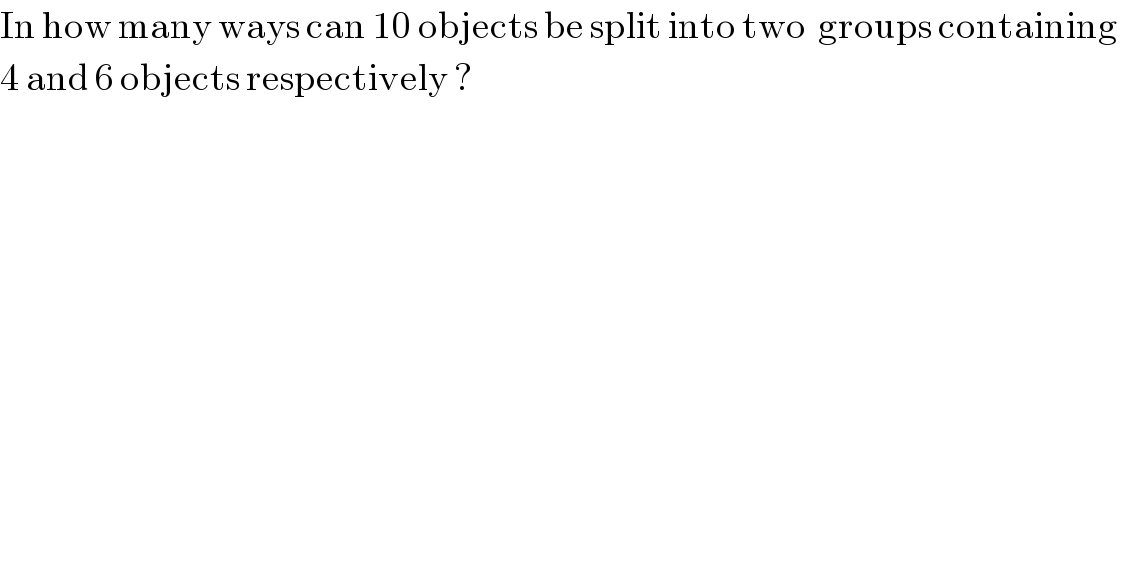
$$\mathrm{In}\:\mathrm{how}\:\mathrm{many}\:\mathrm{ways}\:\mathrm{can}\:\mathrm{10}\:\mathrm{objects}\:\mathrm{be}\:\mathrm{split}\:\mathrm{into}\:\mathrm{two}\:\:\mathrm{groups}\:\mathrm{containing}\: \\ $$$$\mathrm{4}\:\mathrm{and}\:\mathrm{6}\:\mathrm{objects}\:\mathrm{respectively}\:? \\ $$
Answered by sandy_suhendra last updated on 12/Apr/17

$$\mathrm{10C4}\:=\:\frac{\mathrm{10}!}{\mathrm{6}!\:\mathrm{4}!}\:=\mathrm{210} \\ $$$$\mathrm{or}\:\:\mathrm{10C6}\:=\:\mathrm{210} \\ $$
Commented by tawa last updated on 12/Apr/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
