
Previous in Probability and Statistics Next in Probability and Statistics
Question Number 152940 by nadovic last updated on 03/Sep/21
![In bottle manufacturing company, it was observed that 5% of the bottles manufactured were defective. In a random sample of 150 bottles, find probability that (a) exactly 3, (b) between 3 and 6, (c) at most 4, manufactured bottles are defective. [Take e = 2.718]](Q152940.png)
$$\:\mathrm{In}\:\mathrm{bottle}\:\mathrm{manufacturing}\:\mathrm{company},\:\mathrm{it} \\ $$$$\mathrm{was}\:\mathrm{observed}\:\mathrm{that}\:\mathrm{5\%}\:\mathrm{of}\:\mathrm{the}\:\mathrm{bottles} \\ $$$$\mathrm{manufactured}\:\mathrm{were}\:\mathrm{defective}.\:\mathrm{In}\:\mathrm{a}\: \\ $$$$\mathrm{random}\:\mathrm{sample}\:\mathrm{of}\:\mathrm{150}\:\mathrm{bottles},\:\mathrm{find}\: \\ $$$$\mathrm{probability}\:\mathrm{that}\: \\ $$$$\:\left({a}\right)\:\mathrm{exactly}\:\mathrm{3}, \\ $$$$\:\left({b}\right)\:\mathrm{between}\:\mathrm{3}\:\mathrm{and}\:\mathrm{6}, \\ $$$$\:\left({c}\right)\:\mathrm{at}\:\mathrm{most}\:\mathrm{4}, \\ $$$$\:\mathrm{manufactured}\:\mathrm{bottles}\:\mathrm{are}\:\mathrm{defective}. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left[\mathrm{Take}\:\:{e}\:=\:\mathrm{2}.\mathrm{718}\right] \\ $$
Answered by physicstutes last updated on 03/Sep/21
![here we′re gonna use the binomial distribution: p(X=x)=^n C_x p^x q^(n−x) X∼B(150,0.05) (a) p(X=5)=^(150) C_5 (0.05)^5 (0.95)^(150−5) [note: p+q=1] (b) p(3<x<6)= p(X=4)+p(X=5) (c) p(X≤4)= p(X=0)+p(X=1)+p(X=2) +p(X=3)+p(X=4)](Q152968.png)
$$\mathrm{here}\:\mathrm{we}'\mathrm{re}\:\mathrm{gonna}\:\mathrm{use}\:\mathrm{the}\:\mathrm{binomial} \\ $$$$\mathrm{distribution}:\:{p}\left({X}={x}\right)=\:^{{n}} {C}_{{x}} {p}^{{x}} {q}^{{n}−{x}} \\ $$$${X}\sim{B}\left(\mathrm{150},\mathrm{0}.\mathrm{05}\right) \\ $$$$\left(\mathrm{a}\right)\:{p}\left({X}=\mathrm{5}\right)=\:^{\mathrm{150}} {C}_{\mathrm{5}} \left(\mathrm{0}.\mathrm{05}\right)^{\mathrm{5}} \left(\mathrm{0}.\mathrm{95}\right)^{\mathrm{150}−\mathrm{5}} \\ $$$$\left[\boldsymbol{\mathrm{note}}:\:{p}+{q}=\mathrm{1}\right] \\ $$$$\left(\mathrm{b}\right)\:{p}\left(\mathrm{3}<{x}<\mathrm{6}\right)=\:{p}\left({X}=\mathrm{4}\right)+{p}\left({X}=\mathrm{5}\right) \\ $$$$\left(\mathrm{c}\right)\:{p}\left({X}\leqslant\mathrm{4}\right)=\:{p}\left({X}=\mathrm{0}\right)+{p}\left({X}=\mathrm{1}\right)+{p}\left({X}=\mathrm{2}\right) \\ $$$$+{p}\left({X}=\mathrm{3}\right)+{p}\left({X}=\mathrm{4}\right) \\ $$
Commented by nadovic last updated on 04/Sep/21
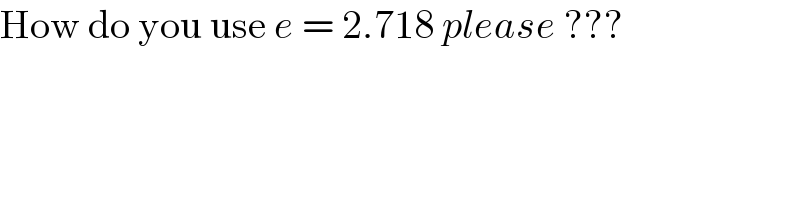
$$\mathrm{How}\:\mathrm{do}\:\mathrm{you}\:\mathrm{use}\:{e}\:=\:\mathrm{2}.\mathrm{718}\:{please}\:??? \\ $$
