
Question Number 15267 by Tinkutara last updated on 09/Jun/17
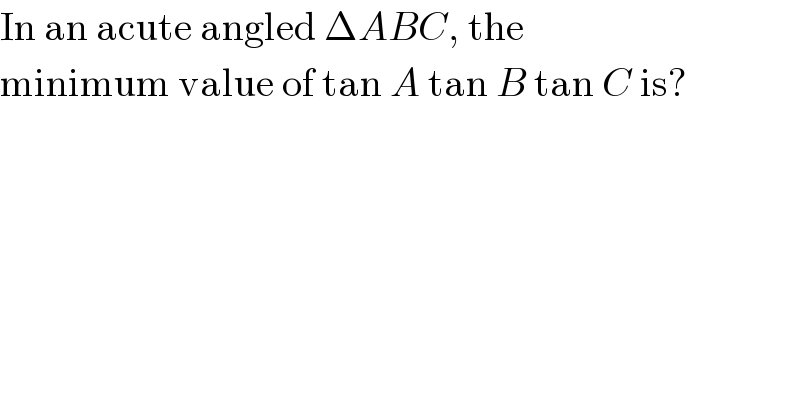
$$\mathrm{In}\:\mathrm{an}\:\mathrm{acute}\:\mathrm{angled}\:\Delta{ABC},\:\mathrm{the} \\ $$$$\mathrm{minimum}\:\mathrm{value}\:\mathrm{of}\:\mathrm{tan}\:{A}\:\mathrm{tan}\:{B}\:\mathrm{tan}\:{C}\:\mathrm{is}? \\ $$
Commented by prakash jain last updated on 09/Jun/17

$${A}=\mathrm{0}.\mathrm{1}°,{B}=\mathrm{89}.\mathrm{5}°,{C}=\mathrm{89}.\mathrm{5}° \\ $$$$\mathrm{tan}\:{A}\mathrm{tan}\:{B}\mathrm{tan}\:{C}=.\mathrm{518} \\ $$$${A}=\mathrm{0}.\mathrm{0000000001}° \\ $$$${B}={C}=\mathrm{89}.\mathrm{99999999995}° \\ $$$$\mathrm{tan}\:{A}\mathrm{tan}\:{B}\mathrm{tan}\:{C}=\mathrm{4}×\mathrm{10}^{−\mathrm{10}} \\ $$$$\mathrm{u}\:\mathrm{can}\:\mathrm{tanAtanBtan}\:\mathrm{C}\:{as}\:{close} \\ $$$${to}\:\mathrm{0}\:{u}\:{want}\:{minimum}\:{is}\:\mathrm{0}. \\ $$$$\mathrm{These}\:\mathrm{calculated}\:\mathrm{values}\:\mathrm{are}\:\mathrm{wrong}\:\mathrm{as} \\ $$$$\mathrm{highlighted}\:\mathrm{in}\:\mathrm{mrW1}\:\mathrm{comment}\:\mathrm{below}. \\ $$
Commented by mrW1 last updated on 09/Jun/17
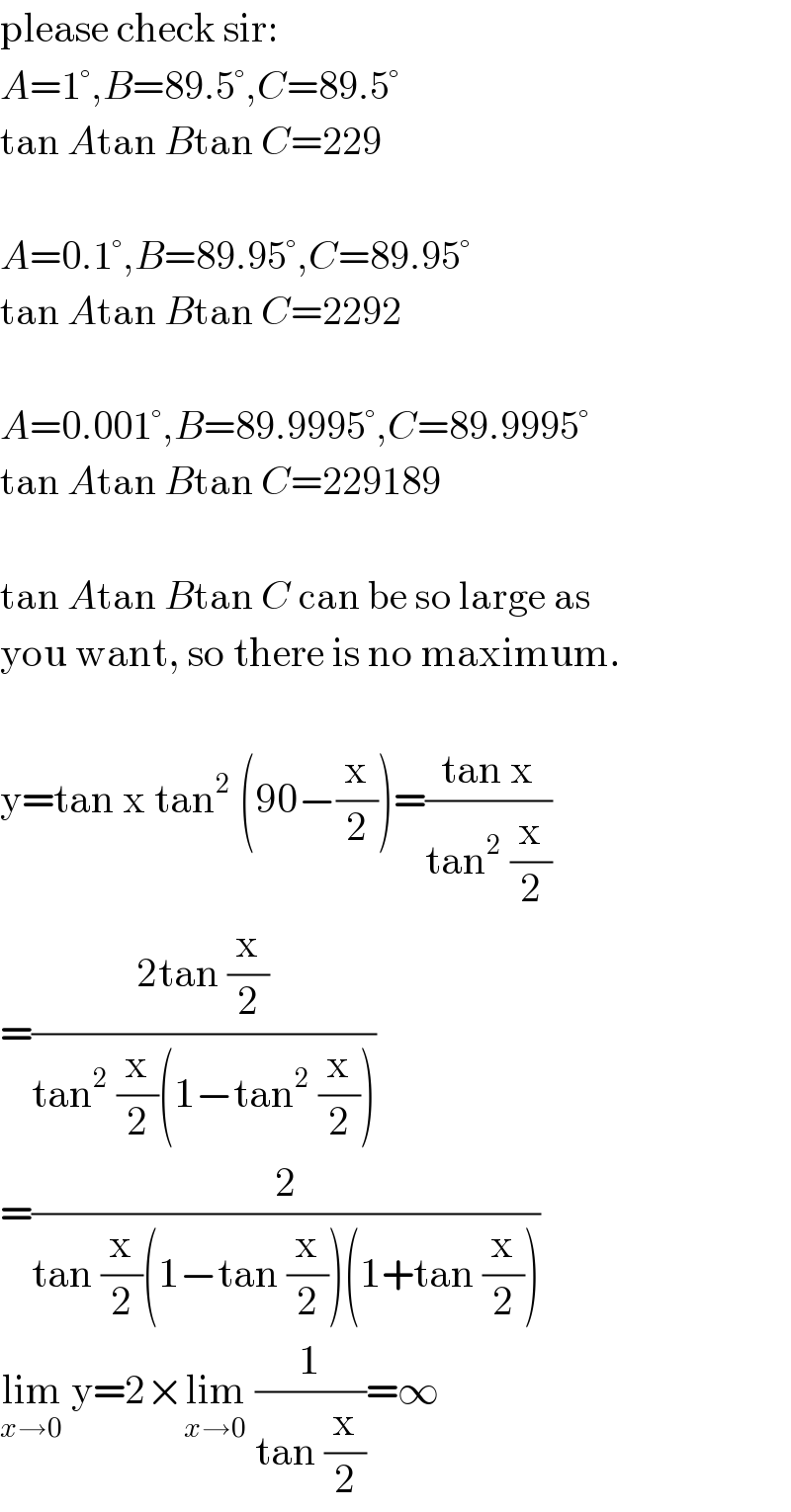
$$\mathrm{please}\:\mathrm{check}\:\mathrm{sir}:\: \\ $$$${A}=\mathrm{1}°,{B}=\mathrm{89}.\mathrm{5}°,{C}=\mathrm{89}.\mathrm{5}° \\ $$$$\mathrm{tan}\:{A}\mathrm{tan}\:{B}\mathrm{tan}\:{C}=\mathrm{229} \\ $$$$ \\ $$$${A}=\mathrm{0}.\mathrm{1}°,{B}=\mathrm{89}.\mathrm{95}°,{C}=\mathrm{89}.\mathrm{95}° \\ $$$$\mathrm{tan}\:{A}\mathrm{tan}\:{B}\mathrm{tan}\:{C}=\mathrm{2292} \\ $$$$ \\ $$$${A}=\mathrm{0}.\mathrm{001}°,{B}=\mathrm{89}.\mathrm{9995}°,{C}=\mathrm{89}.\mathrm{9995}° \\ $$$$\mathrm{tan}\:{A}\mathrm{tan}\:{B}\mathrm{tan}\:{C}=\mathrm{229189} \\ $$$$ \\ $$$$\mathrm{tan}\:{A}\mathrm{tan}\:{B}\mathrm{tan}\:{C}\:\mathrm{can}\:\mathrm{be}\:\mathrm{so}\:\mathrm{large}\:\mathrm{as} \\ $$$$\mathrm{you}\:\mathrm{want},\:\mathrm{so}\:\mathrm{there}\:\mathrm{is}\:\mathrm{no}\:\mathrm{maximum}. \\ $$$$ \\ $$$$\mathrm{y}=\mathrm{tan}\:\mathrm{x}\:\mathrm{tan}^{\mathrm{2}} \:\left(\mathrm{90}−\frac{\mathrm{x}}{\mathrm{2}}\right)=\frac{\mathrm{tan}\:\mathrm{x}}{\mathrm{tan}^{\mathrm{2}} \:\frac{\mathrm{x}}{\mathrm{2}}} \\ $$$$=\frac{\mathrm{2tan}\:\frac{\mathrm{x}}{\mathrm{2}}}{\mathrm{tan}^{\mathrm{2}} \:\frac{\mathrm{x}}{\mathrm{2}}\left(\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \:\frac{\mathrm{x}}{\mathrm{2}}\right)} \\ $$$$=\frac{\mathrm{2}}{\mathrm{tan}\:\frac{\mathrm{x}}{\mathrm{2}}\left(\mathrm{1}−\mathrm{tan}\:\frac{\mathrm{x}}{\mathrm{2}}\right)\left(\mathrm{1}+\mathrm{tan}\:\frac{\mathrm{x}}{\mathrm{2}}\right)} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\mathrm{y}=\mathrm{2}×\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}}{\mathrm{tan}\:\frac{\mathrm{x}}{\mathrm{2}}}=\infty \\ $$
Commented by Tinkutara last updated on 09/Jun/17
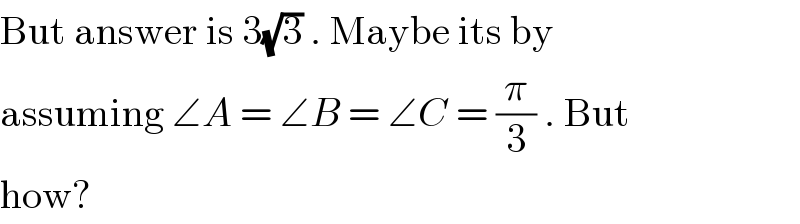
$$\mathrm{But}\:\mathrm{answer}\:\mathrm{is}\:\mathrm{3}\sqrt{\mathrm{3}}\:.\:\mathrm{Maybe}\:\mathrm{its}\:\mathrm{by} \\ $$$$\mathrm{assuming}\:\angle{A}\:=\:\angle{B}\:=\:\angle{C}\:=\:\frac{\pi}{\mathrm{3}}\:.\:\mathrm{But} \\ $$$$\mathrm{how}? \\ $$
Commented by prakash jain last updated on 09/Jun/17
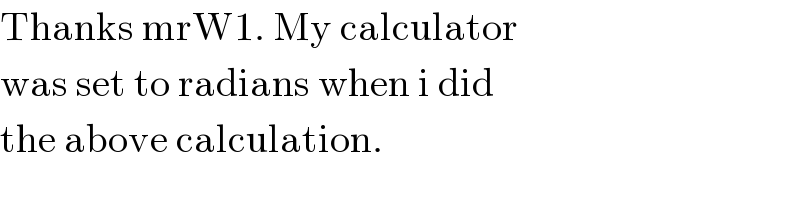
$$\mathrm{Thanks}\:\mathrm{mrW1}.\:\mathrm{My}\:\mathrm{calculator} \\ $$$$\mathrm{was}\:\mathrm{set}\:\mathrm{to}\:\mathrm{radians}\:\mathrm{when}\:\mathrm{i}\:\mathrm{did} \\ $$$$\mathrm{the}\:\mathrm{above}\:\mathrm{calculation}. \\ $$
Commented by prakash jain last updated on 10/Jun/17
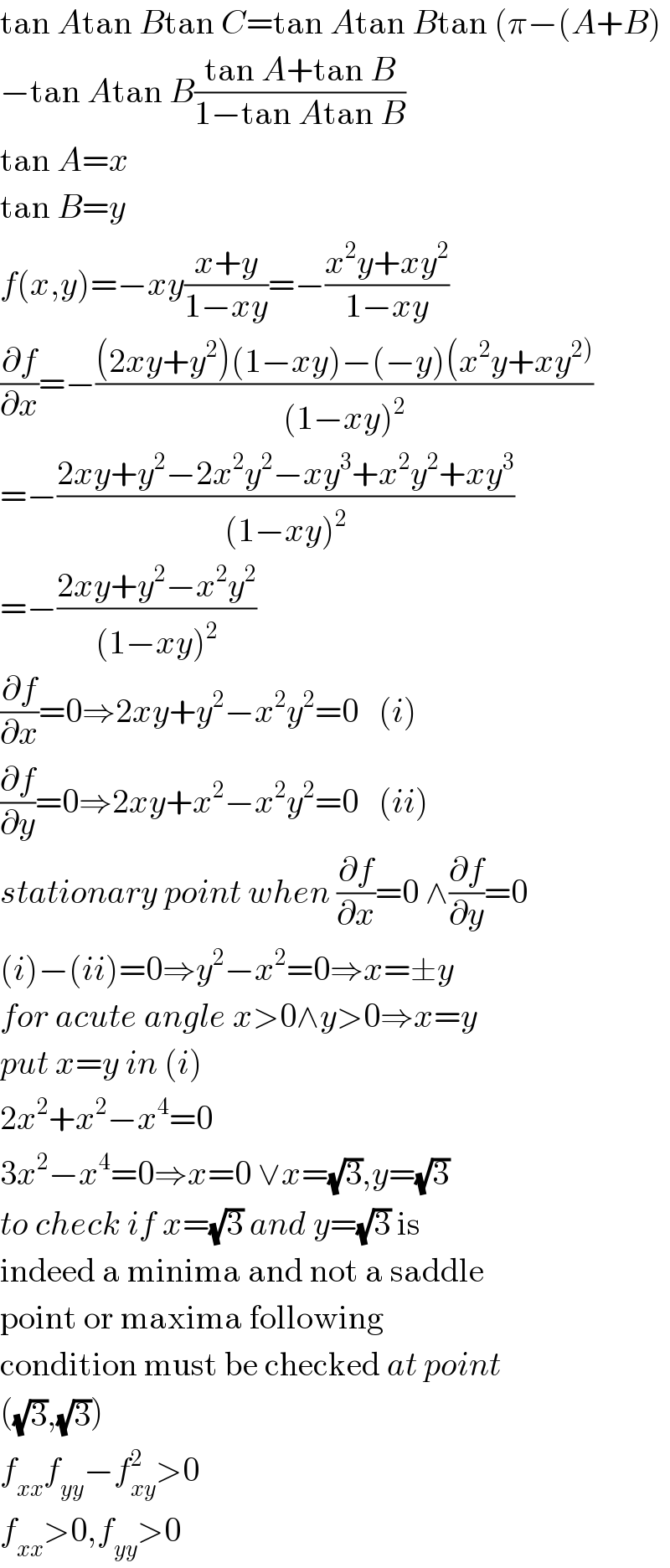
$$\mathrm{tan}\:{A}\mathrm{tan}\:{B}\mathrm{tan}\:{C}=\mathrm{tan}\:{A}\mathrm{tan}\:{B}\mathrm{tan}\:\left(\pi−\left({A}+{B}\right)\right. \\ $$$$−\mathrm{tan}\:{A}\mathrm{tan}\:{B}\frac{\mathrm{tan}\:{A}+\mathrm{tan}\:{B}}{\mathrm{1}−\mathrm{tan}\:{A}\mathrm{tan}\:{B}} \\ $$$$\mathrm{tan}\:{A}={x} \\ $$$$\mathrm{tan}\:{B}={y} \\ $$$${f}\left({x},{y}\right)=−{xy}\frac{{x}+{y}}{\mathrm{1}−{xy}}=−\frac{{x}^{\mathrm{2}} {y}+{xy}^{\mathrm{2}} }{\mathrm{1}−{xy}} \\ $$$$\frac{\partial{f}}{\partial{x}}=−\frac{\left(\mathrm{2}{xy}+{y}^{\mathrm{2}} \right)\left(\mathrm{1}−{xy}\right)−\left(−{y}\right)\left({x}^{\mathrm{2}} {y}+{xy}^{\left.\mathrm{2}\right)} \right.}{\left(\mathrm{1}−{xy}\right)^{\mathrm{2}} } \\ $$$$=−\frac{\mathrm{2}{xy}+{y}^{\mathrm{2}} −\mathrm{2}{x}^{\mathrm{2}} {y}^{\mathrm{2}} −{xy}^{\mathrm{3}} +{x}^{\mathrm{2}} {y}^{\mathrm{2}} +{xy}^{\mathrm{3}} }{\left(\mathrm{1}−{xy}\right)^{\mathrm{2}} } \\ $$$$=−\frac{\mathrm{2}{xy}+{y}^{\mathrm{2}} −{x}^{\mathrm{2}} {y}^{\mathrm{2}} }{\left(\mathrm{1}−{xy}\right)^{\mathrm{2}} } \\ $$$$\frac{\partial{f}}{\partial{x}}=\mathrm{0}\Rightarrow\mathrm{2}{xy}+{y}^{\mathrm{2}} −{x}^{\mathrm{2}} {y}^{\mathrm{2}} =\mathrm{0}\:\:\:\left({i}\right) \\ $$$$\frac{\partial{f}}{\partial{y}}=\mathrm{0}\Rightarrow\mathrm{2}{xy}+{x}^{\mathrm{2}} −{x}^{\mathrm{2}} {y}^{\mathrm{2}} =\mathrm{0}\:\:\:\left({ii}\right) \\ $$$${stationary}\:{point}\:{when}\:\frac{\partial{f}}{\partial{x}}=\mathrm{0}\:\wedge\frac{\partial{f}}{\partial{y}}=\mathrm{0} \\ $$$$\left({i}\right)−\left({ii}\right)=\mathrm{0}\Rightarrow{y}^{\mathrm{2}} −{x}^{\mathrm{2}} =\mathrm{0}\Rightarrow{x}=\pm{y} \\ $$$${for}\:{acute}\:{angle}\:{x}>\mathrm{0}\wedge{y}>\mathrm{0}\Rightarrow{x}={y} \\ $$$${put}\:{x}={y}\:{in}\:\left({i}\right) \\ $$$$\mathrm{2}{x}^{\mathrm{2}} +{x}^{\mathrm{2}} −{x}^{\mathrm{4}} =\mathrm{0} \\ $$$$\mathrm{3}{x}^{\mathrm{2}} −{x}^{\mathrm{4}} =\mathrm{0}\Rightarrow{x}=\mathrm{0}\:\vee{x}=\sqrt{\mathrm{3}},{y}=\sqrt{\mathrm{3}} \\ $$$${to}\:{check}\:{if}\:{x}=\sqrt{\mathrm{3}}\:{and}\:{y}=\sqrt{\mathrm{3}}\:\mathrm{is} \\ $$$$\mathrm{indeed}\:\mathrm{a}\:\mathrm{minima}\:\mathrm{and}\:\mathrm{not}\:\mathrm{a}\:\mathrm{saddle} \\ $$$$\mathrm{point}\:\mathrm{or}\:\mathrm{maxima}\:\mathrm{following} \\ $$$$\mathrm{condition}\:\mathrm{must}\:\mathrm{be}\:\mathrm{checked}\:{at}\:{point} \\ $$$$\left(\sqrt{\mathrm{3}},\sqrt{\mathrm{3}}\right) \\ $$$${f}_{{xx}} {f}_{{yy}} −{f}_{{xy}} ^{\mathrm{2}} >\mathrm{0} \\ $$$${f}_{{xx}} >\mathrm{0},{f}_{{yy}} >\mathrm{0} \\ $$
Commented by mrW1 last updated on 09/Jun/17
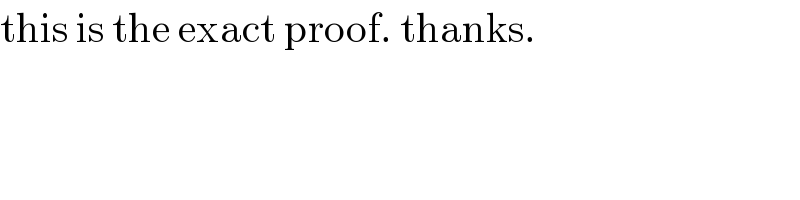
$$\mathrm{this}\:\mathrm{is}\:\mathrm{the}\:\mathrm{exact}\:\mathrm{proof}.\:\mathrm{thanks}. \\ $$
Answered by mrW1 last updated on 09/Jun/17

$$\mathrm{Due}\:\mathrm{to}\:\mathrm{the}\:\mathrm{symmetry}\:\mathrm{the}\:\mathrm{minimum} \\ $$$$\mathrm{occurs}\:\mathrm{when}\:\mathrm{all}\:\mathrm{variables}\:\mathrm{are}\:\mathrm{equal}, \\ $$$$\mathrm{i}.\mathrm{e}.\:\mathrm{A}=\mathrm{B}=\mathrm{C}=\mathrm{60}° \\ $$$$\mathrm{tan}\:\mathrm{A}\:\mathrm{tan}\:\mathrm{B}\:\mathrm{tan}\:\mathrm{C}=\sqrt{\mathrm{3}}×\sqrt{\mathrm{3}}×\sqrt{\mathrm{3}}=\mathrm{3}\sqrt{\mathrm{3}} \\ $$$$ \\ $$$$\mathrm{This}\:\mathrm{can}\:\mathrm{be}\:\mathrm{proved}\:\mathrm{as}\:\mathrm{following}. \\ $$$$\mathrm{To}\:\mathrm{make}\:\mathrm{the}\:\mathrm{thing}\:\mathrm{simple}\:\mathrm{let}\:\mathrm{us}\:\mathrm{keep} \\ $$$$\mathrm{C}\:\mathrm{unchanged}\:\mathrm{and}\:\mathrm{see}\:\mathrm{what}\:\mathrm{happens} \\ $$$$\mathrm{if}\:\:\mathrm{A}\:\mathrm{and}\:\mathrm{B}\:\mathrm{are}\:\mathrm{different}\:\mathrm{from}\:\mathrm{60}°. \\ $$$$ \\ $$$$\mathrm{When}\:\mathrm{A}=\mathrm{B}=\mathrm{60}°,\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{tan}\:\mathrm{A}\:\mathrm{tan}\:\mathrm{B}=\sqrt{\mathrm{3}}×\sqrt{\mathrm{3}}=\mathrm{3} \\ $$$$ \\ $$$$\mathrm{Whenn}\:\mathrm{A}\:\mathrm{and}\:\mathrm{B}\:\mathrm{differ}\:\mathrm{from}\:\mathrm{60}°,\:\mathrm{let}'\mathrm{s} \\ $$$$\mathrm{say}\:\mathrm{A}=\mathrm{60}°+\delta\:\mathrm{and}\:\mathrm{consequently}\: \\ $$$$\mathrm{B}=\mathrm{69}°−\delta,\:\mathrm{then} \\ $$$$\mathrm{tan}\:\mathrm{A}\:\mathrm{tan}\:\mathrm{B}=\mathrm{tan}\:\left(\mathrm{60}+\delta\right)\:\mathrm{tan}\:\left(\mathrm{60}−\delta\right) \\ $$$$=\frac{\mathrm{tan}\:\mathrm{60}+\mathrm{tan}\:\delta}{\mathrm{1}−\mathrm{tan}\:\mathrm{60}\:\mathrm{tan}\:\delta}×\frac{\mathrm{tan}\:\mathrm{60}−\mathrm{tan}\:\delta}{\mathrm{1}+\mathrm{tan}\:\mathrm{60}\:\mathrm{tan}\:\delta} \\ $$$$=\frac{\mathrm{tan}^{\mathrm{2}} \:\mathrm{60}−\mathrm{tan}^{\mathrm{2}} \:\delta}{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \:\mathrm{60}\:\mathrm{tan}^{\mathrm{2}} \:\delta} \\ $$$$=\frac{\mathrm{3}−\mathrm{tan}^{\mathrm{2}} \:\delta}{\mathrm{1}−\mathrm{3}\:\mathrm{tan}^{\mathrm{2}} \:\delta}=\frac{\mathrm{3}−\mathrm{9tan}^{\mathrm{2}} \:\delta+\mathrm{8tan}^{\mathrm{2}} \:\delta}{\mathrm{1}−\mathrm{3tan}^{\mathrm{2}} \:\delta} \\ $$$$=\mathrm{3}+\frac{\mathrm{8tan}^{\mathrm{2}} \:\delta}{\mathrm{1}−\mathrm{3tan}^{\mathrm{2}} \:\delta} \\ $$$$\because\:\mathrm{0}<\delta<\mathrm{30}°\:\left(\mathrm{acute}\:\mathrm{triangle}\right) \\ $$$$\mathrm{0}<\mathrm{tan}\:\delta<\frac{\mathrm{1}}{\sqrt{\mathrm{3}}} \\ $$$$\mathrm{0}<\mathrm{tan}^{\mathrm{2}} \:\delta<\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\mathrm{0}<\mathrm{3tan}^{\mathrm{2}} \:\delta<\mathrm{1} \\ $$$$\therefore\mathrm{1}−\mathrm{3tan}^{\mathrm{2}} \:\delta>\mathrm{0} \\ $$$$\Rightarrow\mathrm{3}+\frac{\mathrm{8tan}^{\mathrm{2}} \:\delta}{\mathrm{1}−\mathrm{3tan}^{\mathrm{2}} \:\delta}>\mathrm{3}=\mathrm{tan}\:\mathrm{60}°\:\mathrm{tan}\:\mathrm{60}° \\ $$$$\mathrm{that}\:\mathrm{means}\:\mathrm{when}\:\mathrm{A},\:\mathrm{B}\:\left(\mathrm{and}\:\mathrm{also}\:\mathrm{C}\right) \\ $$$$\mathrm{differ}\:\mathrm{from}\:\mathrm{60}°,\:\mathrm{the}\:\mathrm{value}\:\mathrm{of} \\ $$$$\mathrm{tan}\:\mathrm{A}\:\mathrm{tan}\:\mathrm{B}\:\mathrm{tan}\:\mathrm{C}\:\mathrm{will}\:\mathrm{increase}, \\ $$$$\mathrm{therefore}\:\mathrm{we}\:\mathrm{have}\:\mathrm{its}\:\mathrm{minimum}\:\mathrm{at} \\ $$$$\mathrm{A}=\mathrm{B}=\mathrm{C}=\mathrm{60}°,\:\mathrm{and}\:\mathrm{the}\:\mathrm{minimum} \\ $$$$\mathrm{value}\:\mathrm{is}\:\mathrm{3}\sqrt{\mathrm{3}.} \\ $$
Commented by Tinkutara last updated on 10/Jun/17

$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$
Answered by Tinkutara last updated on 12/Jun/17
![I found the best method: In any ΔABC, we have tan A + tan B + tan C = tan A tan B tan C = x (say) Now (x/3) ≥ (x)^(1/3) [∵ AM ≥ GM] (x^3 /(27)) ≥ x x ≥ 3(√3)](Q15583.png)
$$\mathrm{I}\:\mathrm{found}\:\mathrm{the}\:\mathrm{best}\:\mathrm{method}: \\ $$$$\mathrm{In}\:\mathrm{any}\:\Delta{ABC},\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{tan}\:{A}\:+\:\mathrm{tan}\:{B}\:+\:\mathrm{tan}\:{C}\:=\:\mathrm{tan}\:{A}\:\mathrm{tan}\:{B}\:\mathrm{tan}\:{C} \\ $$$$=\:{x}\:\left(\mathrm{say}\right) \\ $$$$\mathrm{Now}\:\frac{{x}}{\mathrm{3}}\:\geqslant\:\sqrt[{\mathrm{3}}]{{x}}\:\left[\because\:\mathrm{AM}\:\geqslant\:\mathrm{GM}\right] \\ $$$$\frac{{x}^{\mathrm{3}} }{\mathrm{27}}\:\geqslant\:{x} \\ $$$${x}\:\geqslant\:\mathrm{3}\sqrt{\mathrm{3}} \\ $$
