Question and Answers Forum

All Questions      Topic List

Trigonometry Questions

Previous in All Question      Next in All Question      

Previous in Trigonometry      Next in Trigonometry      

Question Number 211672 by MATHEMATICSAM last updated on 15/Sep/24

In a triangle the bisector of the side c is perpendicular to side b. Prove that 2tanC + tanA = 0.

$$\mathrm{In}\:\mathrm{a}\:\mathrm{triangle}\:\mathrm{the}\:\mathrm{bisector}\:\mathrm{of}\:\mathrm{the}\:\mathrm{side}\:{c}\:\mathrm{is} \\ $$$$\mathrm{perpendicular}\:\mathrm{to}\:\mathrm{side}\:{b}.\:\mathrm{Prove}\:\mathrm{that} \\ $$$$\mathrm{2tanC}\:+\:\mathrm{tanA}\:=\:\mathrm{0}. \\ $$

Commented by Frix last updated on 16/Sep/24

If the bisector of a side is perpendicular to the other side ⇒ the angle between these sides is either 0° or 180°. The bisector of the angle c cannot be perpendicular to the side b because it′s the angle between the sides a and b.

$$\mathrm{If}\:\mathrm{the}\:\mathrm{bisector}\:\mathrm{of}\:\mathrm{a}\:{side}\:\mathrm{is}\:\mathrm{perpendicular}\:\mathrm{to} \\ $$$$\mathrm{the}\:\mathrm{other}\:\mathrm{side}\:\Rightarrow\:\mathrm{the}\:\mathrm{angle}\:\mathrm{between}\:\mathrm{these} \\ $$$$\mathrm{sides}\:\mathrm{is}\:\mathrm{either}\:\mathrm{0}°\:\mathrm{or}\:\mathrm{180}°. \\ $$$$\mathrm{The}\:\mathrm{bisector}\:\mathrm{of}\:\mathrm{the}\:{angle}\:{c}\:\mathrm{cannot}\:\mathrm{be} \\ $$$$\mathrm{perpendicular}\:\mathrm{to}\:\mathrm{the}\:\mathrm{side}\:{b}\:\mathrm{because}\:\mathrm{it}'\mathrm{s}\:\mathrm{the} \\ $$$$\mathrm{angle}\:\mathrm{between}\:\mathrm{the}\:\mathrm{sides}\:{a}\:\mathrm{and}\:{b}. \\ $$

Commented by Frix last updated on 16/Sep/24

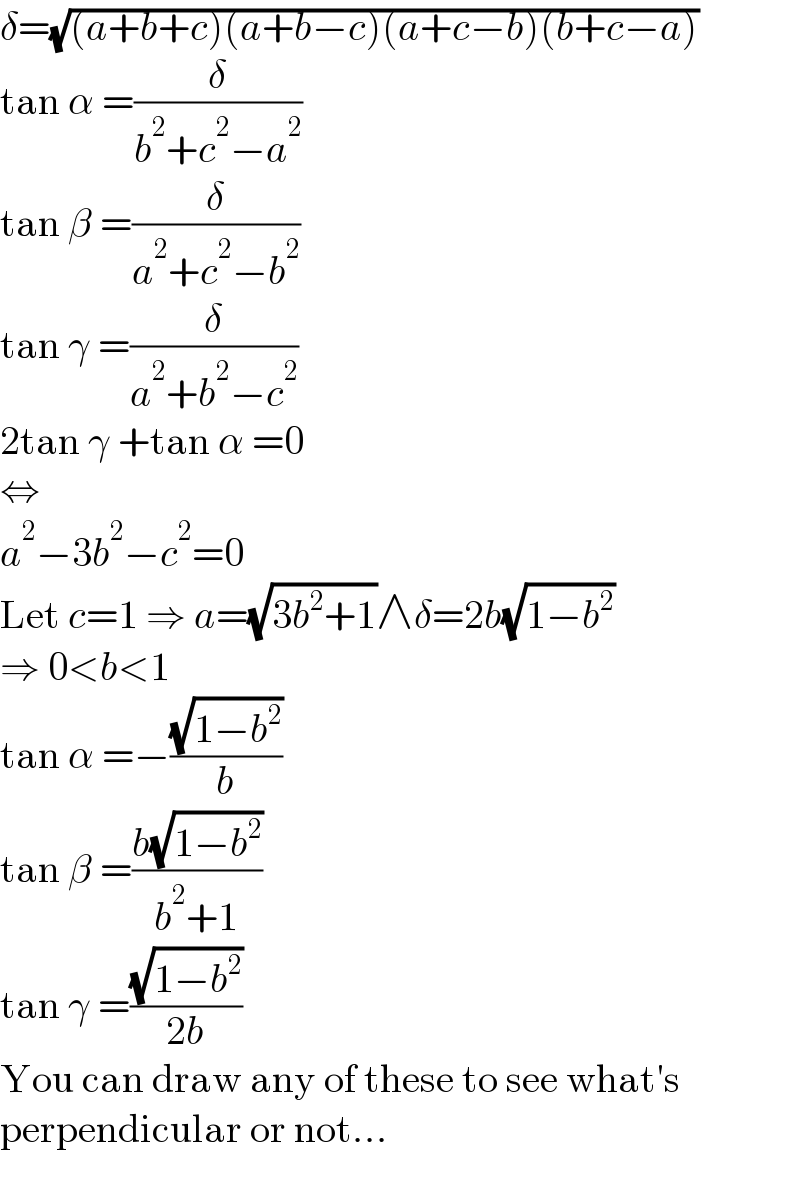
δ=(√((a+b+c)(a+b−c)(a+c−b)(b+c−a))) tan α =(δ/(b^2 +c^2 −a^2 )) tan β =(δ/(a^2 +c^2 −b^2 )) tan γ =(δ/(a^2 +b^2 −c^2 )) 2tan γ +tan α =0 ⇔ a^2 −3b^2 −c^2 =0 Let c=1 ⇒ a=(√(3b^2 +1))∧δ=2b(√(1−b^2 )) ⇒ 0<b<1 tan α =−((√(1−b^2 ))/b) tan β =((b(√(1−b^2 )))/(b^2 +1)) tan γ =((√(1−b^2 ))/(2b)) You can draw any of these to see what′s perpendicular or not...

$$\delta=\sqrt{\left({a}+{b}+{c}\right)\left({a}+{b}−{c}\right)\left({a}+{c}−{b}\right)\left({b}+{c}−{a}\right)} \\ $$$$\mathrm{tan}\:\alpha\:=\frac{\delta}{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{a}^{\mathrm{2}} } \\ $$$$\mathrm{tan}\:\beta\:=\frac{\delta}{{a}^{\mathrm{2}} +{c}^{\mathrm{2}} −{b}^{\mathrm{2}} } \\ $$$$\mathrm{tan}\:\gamma\:=\frac{\delta}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{c}^{\mathrm{2}} } \\ $$$$\mathrm{2tan}\:\gamma\:+\mathrm{tan}\:\alpha\:=\mathrm{0} \\ $$$$\Leftrightarrow \\ $$$${a}^{\mathrm{2}} −\mathrm{3}{b}^{\mathrm{2}} −{c}^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{Let}\:{c}=\mathrm{1}\:\Rightarrow\:{a}=\sqrt{\mathrm{3}{b}^{\mathrm{2}} +\mathrm{1}}\wedge\delta=\mathrm{2}{b}\sqrt{\mathrm{1}−{b}^{\mathrm{2}} } \\ $$$$\Rightarrow\:\mathrm{0}<{b}<\mathrm{1} \\ $$$$\mathrm{tan}\:\alpha\:=−\frac{\sqrt{\mathrm{1}−{b}^{\mathrm{2}} }}{{b}} \\ $$$$\mathrm{tan}\:\beta\:=\frac{{b}\sqrt{\mathrm{1}−{b}^{\mathrm{2}} }}{{b}^{\mathrm{2}} +\mathrm{1}} \\ $$$$\mathrm{tan}\:\gamma\:=\frac{\sqrt{\mathrm{1}−{b}^{\mathrm{2}} }}{\mathrm{2}{b}} \\ $$$$\mathrm{You}\:\mathrm{can}\:\mathrm{draw}\:\mathrm{any}\:\mathrm{of}\:\mathrm{these}\:\mathrm{to}\:\mathrm{see}\:\mathrm{what}'\mathrm{s} \\ $$$$\mathrm{perpendicular}\:\mathrm{or}\:\mathrm{not}... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com