Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 170912 by MathsFan last updated on 03/Jun/22

In a triangle QRS, QR=14cm, RS=12cm and SQ=9cm. An incircle is drawn to touch the three sides of the triangle at X,Y,Z respectively. Find the lenghts QX, RY and SZ.

$$\boldsymbol{\mathrm{In}}\:\boldsymbol{\mathrm{a}}\:\boldsymbol{\mathrm{triangle}}\:\boldsymbol{{QRS}},\:\boldsymbol{{QR}}=\mathrm{14}\boldsymbol{{cm}},\:\boldsymbol{{RS}}=\mathrm{12}\boldsymbol{{cm}} \\ $$$$\boldsymbol{\mathrm{and}}\:\boldsymbol{{SQ}}=\mathrm{9}\boldsymbol{{cm}}.\:\boldsymbol{\mathrm{An}}\:\boldsymbol{\mathrm{incircle}}\:\boldsymbol{\mathrm{is}}\:\boldsymbol{\mathrm{drawn}}\:\boldsymbol{\mathrm{to}} \\ $$$$\boldsymbol{\mathrm{touch}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{three}}\:\boldsymbol{\mathrm{sides}}\:\boldsymbol{\mathrm{of}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{triangle}} \\ $$$$\boldsymbol{\mathrm{at}}\:\boldsymbol{{X}},\boldsymbol{{Y}},\boldsymbol{{Z}}\:\boldsymbol{\mathrm{respectively}}.\:\boldsymbol{\mathrm{Find}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{lenghts}} \\ $$$$\boldsymbol{{QX}},\:\boldsymbol{{RY}}\:\boldsymbol{\mathrm{and}}\:\boldsymbol{{SZ}}. \\ $$

Answered by som(math1967) last updated on 03/Jun/22

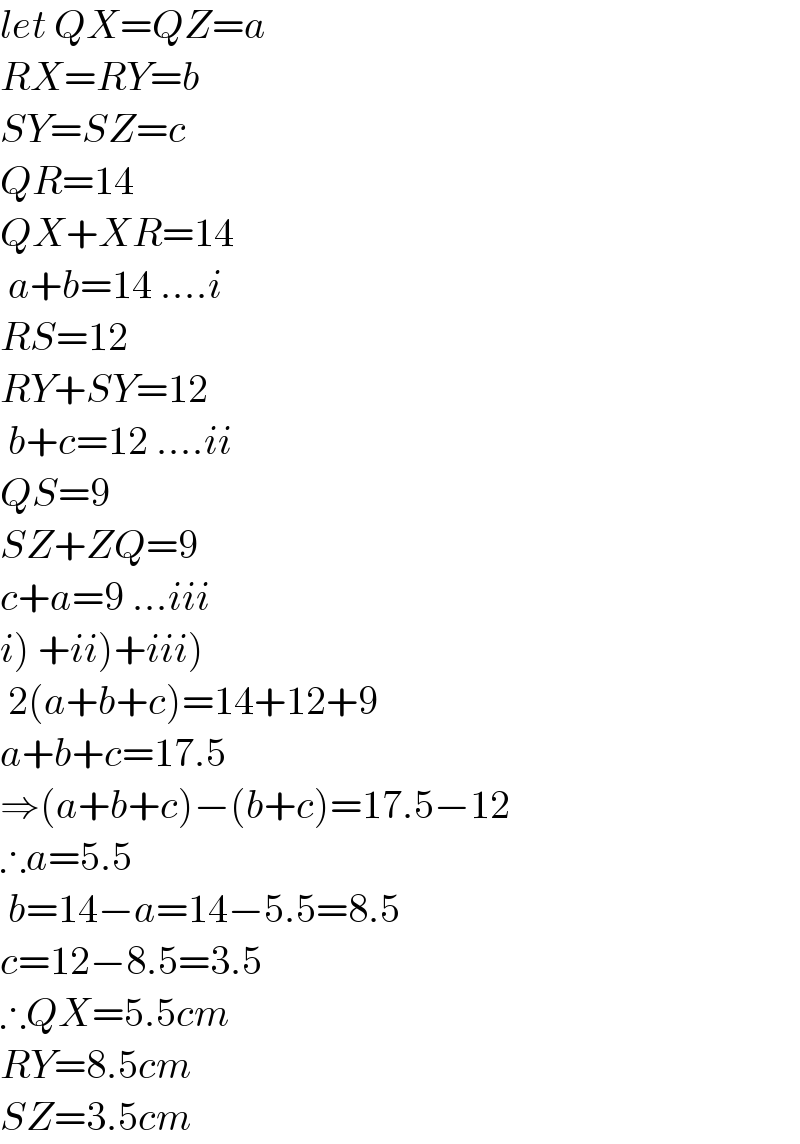
let QX=QZ=a RX=RY=b SY=SZ=c QR=14 QX+XR=14 a+b=14 ....i RS=12 RY+SY=12 b+c=12 ....ii QS=9 SZ+ZQ=9 c+a=9 ...iii i) +ii)+iii) 2(a+b+c)=14+12+9 a+b+c=17.5 ⇒(a+b+c)−(b+c)=17.5−12 ∴a=5.5 b=14−a=14−5.5=8.5 c=12−8.5=3.5 ∴QX=5.5cm RY=8.5cm SZ=3.5cm

$${let}\:{QX}={QZ}={a} \\ $$$${RX}={RY}={b} \\ $$$${SY}={SZ}={c} \\ $$$${QR}=\mathrm{14} \\ $$$${QX}+{XR}=\mathrm{14} \\ $$$$\:{a}+{b}=\mathrm{14}\:....{i} \\ $$$${RS}=\mathrm{12} \\ $$$${RY}+{SY}=\mathrm{12} \\ $$$$\:{b}+{c}=\mathrm{12}\:....{ii} \\ $$$${QS}=\mathrm{9} \\ $$$${SZ}+{ZQ}=\mathrm{9} \\ $$$${c}+{a}=\mathrm{9}\:...{iii} \\ $$$$\left.{i}\left.\right)\left.\:+{ii}\right)+{iii}\right) \\ $$$$\:\mathrm{2}\left({a}+{b}+{c}\right)=\mathrm{14}+\mathrm{12}+\mathrm{9} \\ $$$${a}+{b}+{c}=\mathrm{17}.\mathrm{5} \\ $$$$\Rightarrow\left({a}+{b}+{c}\right)−\left({b}+{c}\right)=\mathrm{17}.\mathrm{5}−\mathrm{12} \\ $$$$\therefore{a}=\mathrm{5}.\mathrm{5} \\ $$$$\:{b}=\mathrm{14}−{a}=\mathrm{14}−\mathrm{5}.\mathrm{5}=\mathrm{8}.\mathrm{5} \\ $$$${c}=\mathrm{12}−\mathrm{8}.\mathrm{5}=\mathrm{3}.\mathrm{5} \\ $$$$\therefore{QX}=\mathrm{5}.\mathrm{5}{cm} \\ $$$${RY}=\mathrm{8}.\mathrm{5}{cm} \\ $$$${SZ}=\mathrm{3}.\mathrm{5}{cm} \\ $$

Commented by som(math1967) last updated on 03/Jun/22

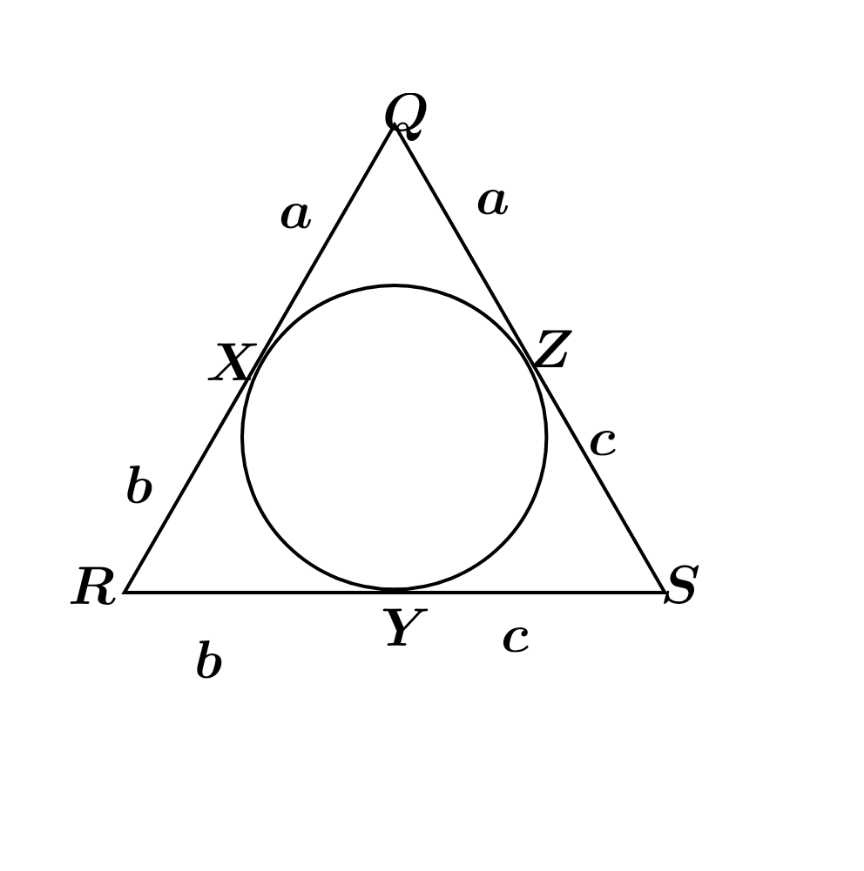
Commented by MathsFan last updated on 03/Jun/22

thank you sir i am very greatful

$${thank}\:{you}\:{sir} \\ $$$${i}\:{am}\:{very}\:{greatful} \\ $$

Commented by otchereabdullai@gmail.com last updated on 03/Jun/22

nice!

$$\mathrm{nice}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com