
Question Number 18320 by Tinkutara last updated on 18/Jul/17

$$\mathrm{In}\:\mathrm{a}\:\mathrm{triangle}\:{ABC}\:\mathrm{with}\:\mathrm{fixed}\:\mathrm{base}\:{BC}, \\ $$$$\mathrm{the}\:\mathrm{vertex}\:{A}\:\mathrm{moves}\:\mathrm{such}\:\mathrm{that}\:\mathrm{cos}\:{B}\:+ \\ $$$$\mathrm{cos}\:{C}\:=\:\mathrm{4}\:\mathrm{sin}^{\mathrm{2}} \:\frac{{A}}{\mathrm{2}}\:.\:\mathrm{If}\:{a},\:{b}\:\mathrm{and}\:{c}\:\mathrm{denote} \\ $$$$\mathrm{the}\:\mathrm{lengths}\:\mathrm{of}\:\mathrm{the}\:\mathrm{sides}\:\mathrm{of}\:\mathrm{the}\:\mathrm{triangle} \\ $$$$\mathrm{opposite}\:\mathrm{to}\:\mathrm{the}\:\mathrm{angles}\:{A},\:{B}\:\mathrm{and}\:{C} \\ $$$$\mathrm{respectively},\:\mathrm{then} \\ $$$$\left(\mathrm{1}\right)\:{b}\:+\:{c}\:=\:\mathrm{4}{a} \\ $$$$\left(\mathrm{2}\right)\:{b}\:+\:{c}\:=\:\mathrm{2}{a} \\ $$$$\left(\mathrm{3}\right)\:\mathrm{Locus}\:\mathrm{of}\:\mathrm{point}\:{A}\:\mathrm{is}\:\mathrm{an}\:\mathrm{ellipse} \\ $$$$\left(\mathrm{4}\right)\:\mathrm{Locus}\:\mathrm{of}\:\mathrm{point}\:{A}\:\mathrm{is}\:\mathrm{a}\:\mathrm{pair}\:\mathrm{of}\:\mathrm{straight} \\ $$$$\mathrm{lines} \\ $$
Answered by ajfour last updated on 19/Jul/17
Commented by ajfour last updated on 19/Jul/17
![Given: cos B+cos C=4sin^2 (A/2) and a=constant. ⇒ cos B+cos C=2(1−cos A) cos B=(x/c) , cos C=((a−x)/b) , cos A=((b^2 +c^2 −a^2 )/(2bc)) x^2 +y^2 =c^2 (a−x)^2 +y^2 =b^2 subtracting we get a(2x−a)=−(b+c)(b−c) ⇒ x= (a/2)−(((b+c)(b−c))/(2a)) =((a^2 −(b+c)(b−c))/(2a)) .....(i) from given condition (x/c)+((a−x)/b)=2(1−cos A) ⇒ ((ac+x(b−c))/(bc))=2(1−((b^2 +c^2 −a^2 )/(2bc))) replacing x from (i): (( a)/b)+(((b−c)/(2abc)))[a^2 −(b+c)(b−c)] =2[((2bc−(b^2 +c^2 )+a^2 )/(2bc))] 2a^2 c+a^2 (b−c)−(b−c)^2 (b+c) =−2a(b−c)^2 +2a^3 ⇒a^2 (2c+b−c−2a) =(b−c)^2 (b+c−2a) a^2 (b+c−2a)=(b−c)^2 (b+c−2a) ⇒ 2a=b+c or a=∣b−c∣ If we accept : b+c =2a=constant, then locus of A is an ellipse with foci at B and C. If we accept a=∣b−c∣ then A lies on produced BC and on either side.](Q18339.png)
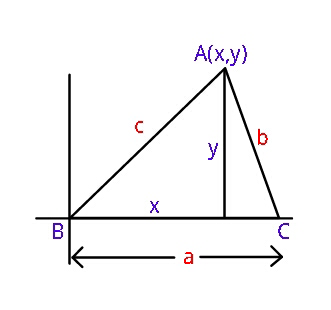
$$\mathrm{Given}:\:\:\:\mathrm{cos}\:\mathrm{B}+\mathrm{cos}\:\mathrm{C}=\mathrm{4sin}\:^{\mathrm{2}} \frac{\mathrm{A}}{\mathrm{2}} \\ $$$$\mathrm{and}\:\mathrm{a}=\mathrm{constant}. \\ $$$$\Rightarrow\:\:\mathrm{cos}\:\mathrm{B}+\mathrm{cos}\:\mathrm{C}=\mathrm{2}\left(\mathrm{1}−\mathrm{cos}\:\mathrm{A}\right) \\ $$$$\mathrm{cos}\:\mathrm{B}=\frac{\mathrm{x}}{\mathrm{c}}\:,\:\:\mathrm{cos}\:\mathrm{C}=\frac{\mathrm{a}−\mathrm{x}}{\mathrm{b}}\:, \\ $$$$\mathrm{cos}\:\mathrm{A}=\frac{\mathrm{b}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} −\mathrm{a}^{\mathrm{2}} }{\mathrm{2bc}} \\ $$$$\:\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} =\mathrm{c}^{\mathrm{2}} \\ $$$$\left(\mathrm{a}−\mathrm{x}\right)^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} =\mathrm{b}^{\mathrm{2}} \\ $$$$\mathrm{subtracting}\:\mathrm{we}\:\mathrm{get} \\ $$$$\:\:\:\mathrm{a}\left(\mathrm{2x}−\mathrm{a}\right)=−\left(\mathrm{b}+\mathrm{c}\right)\left(\mathrm{b}−\mathrm{c}\right) \\ $$$$\Rightarrow\:\:\mathrm{x}=\:\frac{\mathrm{a}}{\mathrm{2}}−\frac{\left(\mathrm{b}+\mathrm{c}\right)\left(\mathrm{b}−\mathrm{c}\right)}{\mathrm{2a}} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{a}^{\mathrm{2}} −\left(\mathrm{b}+\mathrm{c}\right)\left(\mathrm{b}−\mathrm{c}\right)}{\mathrm{2a}}\:\:\:\:.....\left(\mathrm{i}\right) \\ $$$$\mathrm{from}\:\mathrm{given}\:\mathrm{condition} \\ $$$$\:\:\frac{\mathrm{x}}{\mathrm{c}}+\frac{\mathrm{a}−\mathrm{x}}{\mathrm{b}}=\mathrm{2}\left(\mathrm{1}−\mathrm{cos}\:\mathrm{A}\right) \\ $$$$\Rightarrow\:\:\:\frac{\mathrm{ac}+\mathrm{x}\left(\mathrm{b}−\mathrm{c}\right)}{\mathrm{bc}}=\mathrm{2}\left(\mathrm{1}−\frac{\mathrm{b}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} −\mathrm{a}^{\mathrm{2}} }{\mathrm{2bc}}\right) \\ $$$$\mathrm{replacing}\:\mathrm{x}\:\mathrm{from}\:\left(\mathrm{i}\right): \\ $$$$\:\frac{\:\mathrm{a}}{\mathrm{b}}+\left(\frac{\mathrm{b}−\mathrm{c}}{\mathrm{2abc}}\right)\left[\mathrm{a}^{\mathrm{2}} −\left(\mathrm{b}+\mathrm{c}\right)\left(\mathrm{b}−\mathrm{c}\right)\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}\left[\frac{\mathrm{2bc}−\left(\mathrm{b}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} \right)+\mathrm{a}^{\mathrm{2}} }{\mathrm{2bc}}\right] \\ $$$$\mathrm{2a}^{\mathrm{2}} \mathrm{c}+\mathrm{a}^{\mathrm{2}} \left(\mathrm{b}−\mathrm{c}\right)−\left(\mathrm{b}−\mathrm{c}\right)^{\mathrm{2}} \left(\mathrm{b}+\mathrm{c}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=−\mathrm{2a}\left(\mathrm{b}−\mathrm{c}\right)^{\mathrm{2}} +\mathrm{2a}^{\mathrm{3}} \\ $$$$\Rightarrow\mathrm{a}^{\mathrm{2}} \left(\mathrm{2c}+\mathrm{b}−\mathrm{c}−\mathrm{2a}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left(\mathrm{b}−\mathrm{c}\right)^{\mathrm{2}} \left(\mathrm{b}+\mathrm{c}−\mathrm{2a}\right) \\ $$$$\:\mathrm{a}^{\mathrm{2}} \left(\mathrm{b}+\mathrm{c}−\mathrm{2a}\right)=\left(\mathrm{b}−\mathrm{c}\right)^{\mathrm{2}} \left(\mathrm{b}+\mathrm{c}−\mathrm{2a}\right) \\ $$$$\Rightarrow\:\:\mathrm{2a}=\mathrm{b}+\mathrm{c}\:\:\:\mathrm{or}\:\:\:\:\mathrm{a}=\mid\mathrm{b}−\mathrm{c}\mid \\ $$$$\mathrm{If}\:\mathrm{we}\:\mathrm{accept}\::\:\mathrm{b}+\mathrm{c}\:=\mathrm{2a}=\mathrm{constant}, \\ $$$$\mathrm{then}\:\mathrm{locus}\:\mathrm{of}\:\mathrm{A}\:\mathrm{is}\:\mathrm{an}\:\mathrm{ellipse}\:\mathrm{with} \\ $$$$\mathrm{foci}\:\mathrm{at}\:\mathrm{B}\:\mathrm{and}\:\mathrm{C}. \\ $$$$\:\mathrm{If}\:\mathrm{we}\:\mathrm{accept}\:\mathrm{a}=\mid\mathrm{b}−\mathrm{c}\mid\:\mathrm{then}\:\mathrm{A}\:\mathrm{lies}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\mathrm{on}\:\mathrm{produced}\:\mathrm{BC}\:\mathrm{and}\:\mathrm{on}\:\mathrm{either}\:\mathrm{side}. \\ $$
Commented by Tinkutara last updated on 19/Jul/17

$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$
