
Question Number 134097 by bobhans last updated on 27/Feb/21
$$\mathrm{In}\:\mathrm{a}\:\mathrm{square}\:\mathrm{ABCD}\:,\:\mathrm{a}\:\mathrm{triangle} \\ $$$$\mathrm{APQ}\:\mathrm{inscribed}\:\mathrm{in}\:\mathrm{it}.\:\mathrm{AP}=\mathrm{4}\:\mathrm{cm}, \\ $$$$\mathrm{PQ}=\mathrm{3}\:\mathrm{cm}\:\mathrm{and}\:\mathrm{AQ}=\mathrm{5}\:\mathrm{cm}.\:\mathrm{Point} \\ $$$$\mathrm{P}\:\mathrm{is}\:\mathrm{on}\:\mathrm{the}\:\mathrm{side}\:\mathrm{BC}\:\mathrm{and}\:\mathrm{point}\:\mathrm{Q} \\ $$$$\mathrm{is}\:\mathrm{on}\:\mathrm{side}\:\mathrm{CD}.\:\mathrm{Find}\:\mathrm{the}\:\mathrm{area}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{square}\:\mathrm{ABCD}. \\ $$
Answered by mr W last updated on 27/Feb/21
Commented by mr W last updated on 27/Feb/21

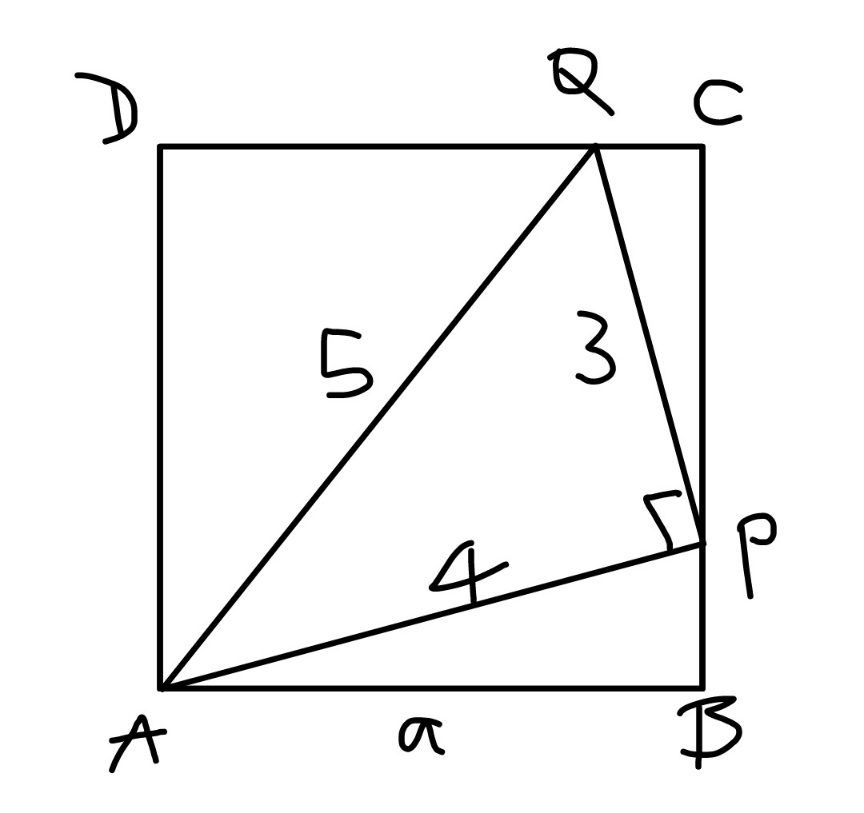
$${BP}=\sqrt{\mathrm{4}^{\mathrm{2}} −{a}^{\mathrm{2}} } \\ $$$$\frac{{PC}}{\mathrm{3}}=\frac{{a}}{\mathrm{4}} \\ $$$$\Rightarrow{PC}=\frac{\mathrm{3}{a}}{\mathrm{4}} \\ $$$$\sqrt{\mathrm{4}^{\mathrm{2}} −{a}^{\mathrm{2}} }+\frac{\mathrm{3}{a}}{\mathrm{4}}={a} \\ $$$$\mathrm{4}^{\mathrm{2}} −{a}^{\mathrm{2}} =\frac{{a}^{\mathrm{2}} }{\mathrm{16}} \\ $$$${a}^{\mathrm{2}} =\frac{\mathrm{16}^{\mathrm{2}} }{\mathrm{17}} \\ $$$$\Rightarrow{a}=\frac{\mathrm{16}}{\:\sqrt{\mathrm{17}}} \\ $$$${area}\:{of}\:{ABCD}={a}^{\mathrm{2}} =\frac{\mathrm{16}^{\mathrm{2}} }{\mathrm{17}}=\frac{\mathrm{256}}{\mathrm{17}}\approx\mathrm{15}.\mathrm{05} \\ $$
Commented by bobhans last updated on 28/Feb/21

$$\mathrm{thanks} \\ $$
Commented by otchereabdullai@gmail.com last updated on 12/Mar/21

$$\mathrm{Thanks}\:\mathrm{prof}\:\mathrm{w} \\ $$
Answered by liberty last updated on 01/Mar/21
Commented by liberty last updated on 01/Mar/21
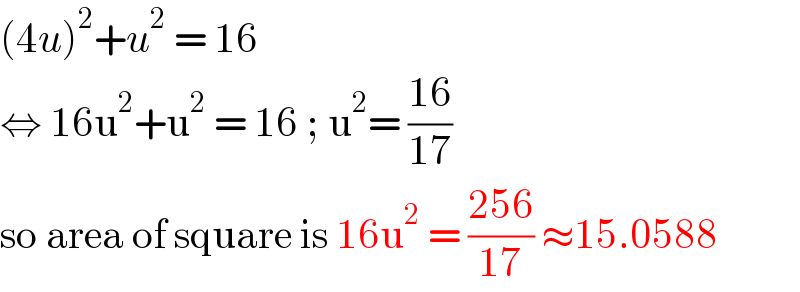
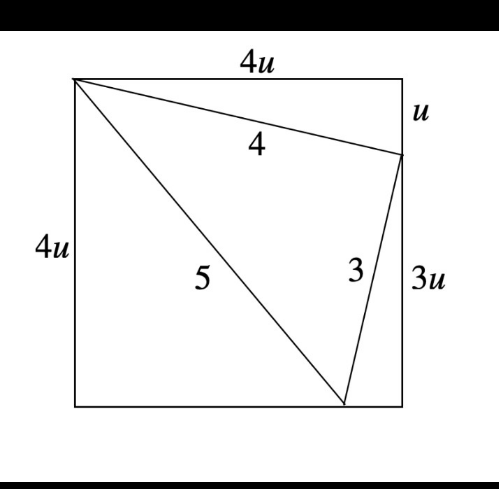
$$\left(\mathrm{4}{u}\right)^{\mathrm{2}} +{u}^{\mathrm{2}} \:=\:\mathrm{16}\: \\ $$$$\Leftrightarrow\:\mathrm{16u}^{\mathrm{2}} +\mathrm{u}^{\mathrm{2}} \:=\:\mathrm{16}\:;\:\mathrm{u}^{\mathrm{2}} =\:\frac{\mathrm{16}}{\mathrm{17}} \\ $$$$\mathrm{so}\:\mathrm{area}\:\mathrm{of}\:\mathrm{square}\:\mathrm{is}\:\mathrm{16u}^{\mathrm{2}} \:=\:\frac{\mathrm{256}}{\mathrm{17}}\:\approx\mathrm{15}.\mathrm{0588} \\ $$
