
Question Number 20599 by Tinkutara last updated on 28/Aug/17

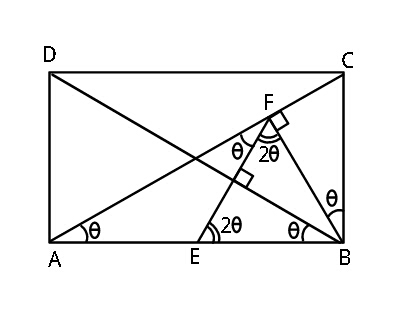
$$\mathrm{In}\:\mathrm{a}\:\mathrm{rectangle}\:{ABCD},\:{E}\:\mathrm{is}\:\mathrm{the}\:\mathrm{midpoint} \\ $$$$\mathrm{of}\:{AB};\:{F}\:\mathrm{is}\:\mathrm{a}\:\mathrm{point}\:\mathrm{on}\:{AC}\:\mathrm{such}\:\mathrm{that}\:{BF} \\ $$$$\mathrm{is}\:\mathrm{perpendicular}\:\mathrm{to}\:{AC};\:\mathrm{and}\:{FE} \\ $$$$\mathrm{perpendicular}\:\mathrm{to}\:{BD}.\:\mathrm{Suppose}\:{BC}\:=\:\mathrm{8}\sqrt{\mathrm{3}}. \\ $$$$\mathrm{Find}\:{AB}. \\ $$
Answered by ajfour last updated on 29/Aug/17
Commented by Tinkutara last updated on 29/Aug/17
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$
Commented by ajfour last updated on 29/Aug/17

$${EF}={AE}={BE}\:\left({radii}\:{of}\:{circle}\right. \\ $$$$\left.{with}\:{E}\:{as}\:{centre}\right) \\ $$$${so}\:\angle{AFE}=\theta \\ $$$$\angle{DBF}=\mathrm{90}°−\mathrm{2}\theta\:,\:{so}\:\angle{EBF}=\mathrm{2}\theta \\ $$$${now}\:\angle{AFE}+\angle{EFB}=\mathrm{90}° \\ $$$${so}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\theta+\mathrm{2}\theta=\mathrm{90}°\:\: \\ $$$$\Rightarrow\:\:\:\:\:\:\mathrm{tan}\:\theta=\frac{{BC}}{{AB}}\:=\frac{\mathrm{8}\sqrt{\mathrm{3}}}{{AB}}\:=\:\frac{\mathrm{1}}{\sqrt{\mathrm{3}}} \\ $$$$\:\:\:\:{or}\:\:\:\boldsymbol{{AB}}=\mathrm{24}\:. \\ $$$$ \\ $$
