
Previous in Permutation and Combination Next in Permutation and Combination
Question Number 178454 by SLVR last updated on 16/Oct/22

$${In}\:{a}\:{chess}\:{board}\:{number}\:{of}\:{unit}\:{squares} \\ $$$$\left.{with}\:\mathrm{1}\right){one}\:{vertex}\:{common}? \\ $$$$\left.\mathrm{2}\right)\mathrm{2}\:{vertices}\:{common}?? \\ $$$$\left.\mathrm{3}\right)\mathrm{2}\:{sides}\:{common}?? \\ $$
Answered by SLVR last updated on 16/Oct/22

$${kindly}\:{help}\:{me} \\ $$
Commented by mr W last updated on 16/Oct/22
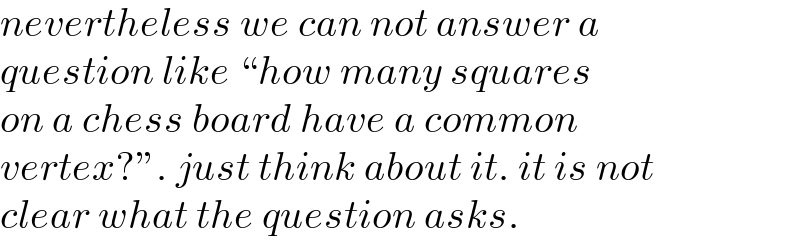
$${nevertheless}\:{we}\:{can}\:{not}\:{answer}\:{a} \\ $$$${question}\:{like}\:``{how}\:{many}\:{squares} \\ $$$${on}\:{a}\:{chess}\:{board}\:{have}\:{a}\:{common} \\ $$$${vertex}?''.\:{just}\:{think}\:{about}\:{it}.\:{it}\:{is}\:{not} \\ $$$${clear}\:{what}\:{the}\:{question}\:{asks}. \\ $$
Commented by mr W last updated on 16/Oct/22

$${i}\:{think}\:{your}\:{question}\:{is}\:{not}\:{clear}. \\ $$$${at}\:{most}\:\mathrm{4}\:{unit}\:{squares}\:{have}\:{a}\:{common} \\ $$$${vertex}.\:{at}\:{most}\:\mathrm{2}\:{unit}\:{squres}\:{have}\:\mathrm{2} \\ $$$${common}\:{vertexex}.\:{at}\:{most}\:\mathrm{2}\:{unit} \\ $$$${squares}\:{have}\:{a}\:{common}\:{side}. \\ $$
Commented by SLVR last updated on 16/Oct/22

$${Sir}..{it}\:{is}\:{my}\:{luck}\:..{you}\:{are}\:{answering} \\ $$$$....{it}\:{is}\:{not}\:{unit}\:{squares}.. \\ $$$${but}\:{sqares}\:{of}\:{any}\:{size}..{typo}.. \\ $$$${kidly}\:{forgive}?{my}\:{mistake}.. \\ $$
Answered by Acem last updated on 16/Oct/22

$$\left.\mathrm{1}\right)\:{One}\:{vertex}\:{common}:\:{on}\:{four}\:{board}\:{edges} \\ $$$$\:{Each}\:{vertex}\:{is}\:{formed}\:{of}\:\mathrm{2}\:{squares} \\ $$$$\:{Num}_{\mathrm{1}\:{ver}.{com}} =\:\left({n}−\mathrm{1}\right)×\mathrm{4}_{{edge}} =\:\mathrm{28}\:\boldsymbol{{vertices}}\:;{n}=\mathrm{8} \\ $$$$\:{if}\:{you}\:{want}\:{number}\:{of}\:{squares}\:{multiply}\:{by}\:\mathrm{2} \\ $$$$ \\ $$$$\left.\mathrm{2}\right)\:{Vertices}\:{common}:\:{inside}\:{board} \\ $$$$\:{Each}\:{vertex}\:{is}\:{formed}\:{of}\:\mathrm{4}\:{squares} \\ $$$$\:{Num}_{{vertices}\:{com}} =\:\left({n}−\mathrm{1}\right)^{\mathrm{2}} =\:\mathrm{49}\:\boldsymbol{{vertices}}_{{of}\:{each}\:\mathrm{4}\:{squ}.} \\ $$$$\: \\ $$$$\left.\mathrm{3}\right)\:{Sides}\:{common}:\:{inside}\:{board} \\ $$$$\:{Each}\:{side}\:{is}\:{formed}\:{of}\:\mathrm{2}\:{squares} \\ $$$$\:{Num}_{{sides}\:{com}} =\:\mathrm{2}{n}\left({n}−\mathrm{1}\right)=\:\mathrm{112}\:\boldsymbol{{sides}}_{{of}\:{each}\:\mathrm{2}\:{squ}.} \\ $$$$ \\ $$
