Question and Answers Forum

All Questions      Topic List

Logic Questions

Previous in All Question      Next in All Question      

Previous in Logic      Next in Logic      

Question Number 92687 by Ar Brandon last updated on 08/May/20

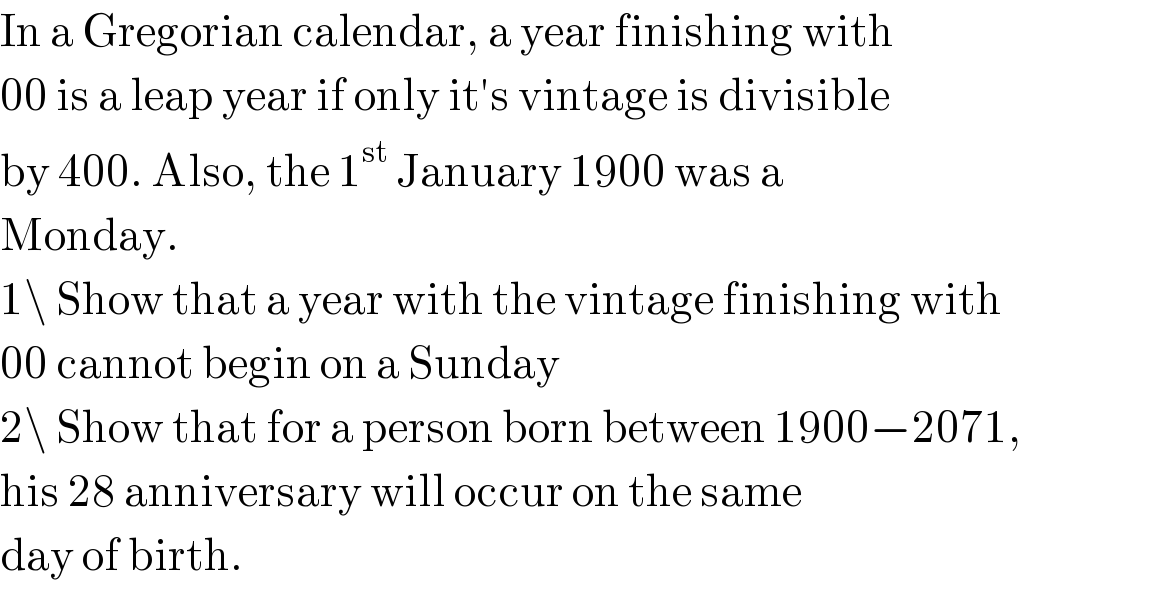
$$\mathrm{In}\mathrm{a}\mathrm{Gregorian}\mathrm{calendar},\mathrm{a}\mathrm{year}\mathrm{finishing}\mathrm{with}$$$$00\mathrm{is}\mathrm{a}\mathrm{leap}\mathrm{year}\mathrm{if}\mathrm{only}{\mathrm{it}}^{\prime }\mathrm{s}\mathrm{vintage}\mathrm{is}\mathrm{divisible}$$$$\mathrm{by}400.\mathrm{Also},\mathrm{the}{1}^{\mathrm{st}}\mathrm{January}1900\mathrm{was}\mathrm{a}$$$$\mathrm{Monday}.$$$$1\mathrm{\setminus }\mathrm{Show}\mathrm{that}\mathrm{a}\mathrm{year}\mathrm{with}\mathrm{the}\mathrm{vintage}\mathrm{finishing}\mathrm{with}$$$$00\mathrm{cannot}\mathrm{begin}\mathrm{on}\mathrm{a}\mathrm{Sunday}$$$$2\mathrm{\setminus }\mathrm{Show}\mathrm{that}\mathrm{for}\mathrm{a}\mathrm{person}\mathrm{born}\mathrm{between}1900-2071,$$$$\mathrm{his}28\mathrm{anniversary}\mathrm{will}\mathrm{occur}\mathrm{on}\mathrm{the}\mathrm{same}$$$$\mathrm{day}\mathrm{of}\mathrm{birth}.$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com