
Question Number 20925 by dk3029943@gmail.com last updated on 08/Sep/17
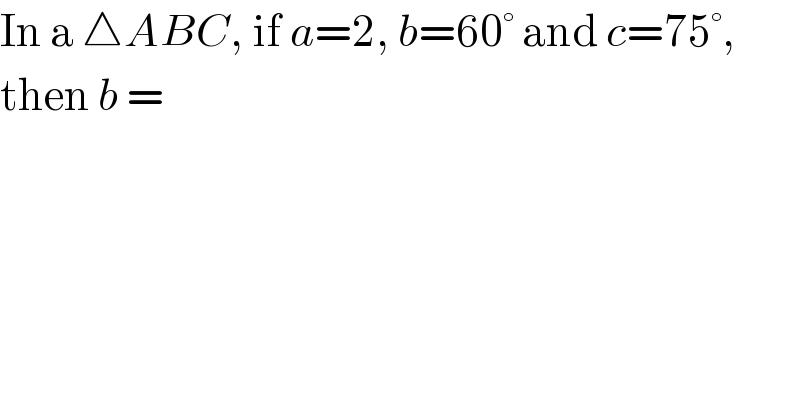
$$\mathrm{In}\:\mathrm{a}\:\bigtriangleup{ABC},\:\mathrm{if}\:{a}=\mathrm{2},\:{b}=\mathrm{60}°\:\mathrm{and}\:{c}=\mathrm{75}°, \\ $$$$\mathrm{then}\:{b}\:= \\ $$
Answered by Joel577 last updated on 08/Sep/17
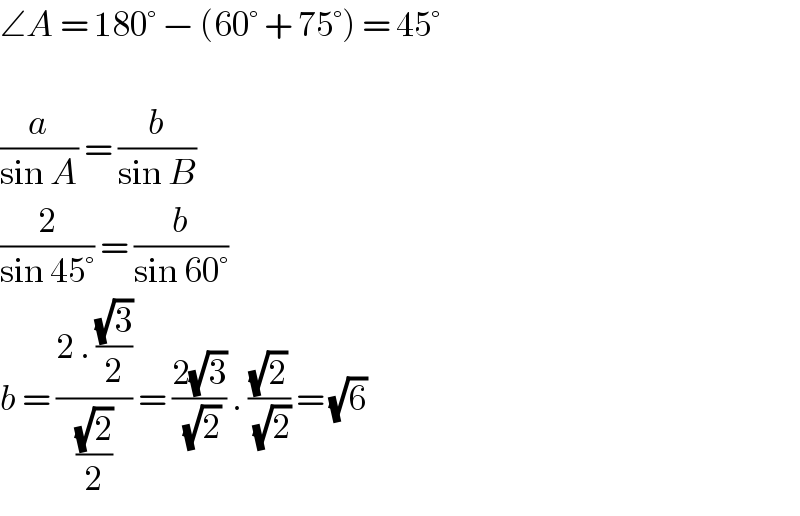
$$\angle{A}\:=\:\mathrm{180}°\:−\:\left(\mathrm{60}°\:+\:\mathrm{75}°\right)\:=\:\mathrm{45}° \\ $$$$ \\ $$$$\frac{{a}}{\mathrm{sin}\:{A}}\:=\:\frac{{b}}{\mathrm{sin}\:{B}} \\ $$$$\frac{\mathrm{2}}{\mathrm{sin}\:\mathrm{45}°}\:=\:\frac{{b}}{\mathrm{sin}\:\mathrm{60}°} \\ $$$${b}\:=\:\frac{\mathrm{2}\:.\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}{\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}}\:=\:\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\sqrt{\mathrm{2}}}\:.\:\frac{\sqrt{\mathrm{2}}}{\sqrt{\mathrm{2}}}\:=\:\sqrt{\mathrm{6}} \\ $$
Answered by $@ty@m last updated on 08/Sep/17
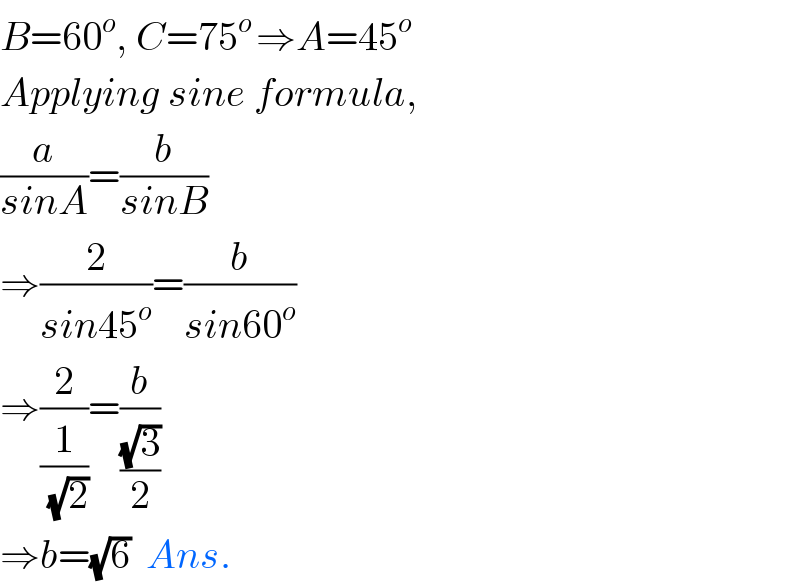
$${B}=\mathrm{60}^{{o}} ,\:{C}=\mathrm{75}^{{o}\:} \Rightarrow{A}=\mathrm{45}^{{o}} \\ $$$${Applying}\:{sine}\:{formula}, \\ $$$$\frac{{a}}{{sinA}}=\frac{{b}}{{sinB}} \\ $$$$\Rightarrow\frac{\mathrm{2}}{{sin}\mathrm{45}^{{o}} }=\frac{{b}}{{sin}\mathrm{60}^{{o}} } \\ $$$$\Rightarrow\frac{\mathrm{2}}{\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}}=\frac{{b}}{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}} \\ $$$$\Rightarrow{b}=\sqrt{\mathrm{6}}\:\:{Ans}. \\ $$
