
Previous in Matrices and Determinants Next in Matrices and Determinants
Question Number 41332 by rahul 19 last updated on 05/Aug/18

$$\mathrm{In}\:\mathrm{Matrices},\: \\ $$$$\mathrm{Is}\:\left(\mathrm{A}^{−\mathrm{1}} \right)\mathrm{B}\:=\:\mathrm{B}\left(\mathrm{A}^{−\mathrm{1}} \right)\:? \\ $$
Commented by rahul 19 last updated on 06/Aug/18

$$\mathrm{ok}\:\mathrm{prof}\:. \\ $$
Commented by candre last updated on 06/Aug/18

$$\begin{vmatrix}{\mathrm{1}}\\{\mathrm{2}}\end{vmatrix}\begin{vmatrix}{\mathrm{1}}&{\mathrm{2}}\end{vmatrix}=\begin{vmatrix}{\mathrm{1}}\\{\mathrm{2}}\end{vmatrix} \\ $$$$\begin{vmatrix}{\mathrm{1}}&{\mathrm{2}}\end{vmatrix}\begin{vmatrix}{\mathrm{1}}\\{\mathrm{2}}\end{vmatrix}=\begin{vmatrix}{\mathrm{3}}\end{vmatrix} \\ $$$$\mathrm{also}\:\mathrm{AB}\:{existing}\:{don}'{t}\:{even}\:{imply}\:{BA}\:{exist} \\ $$$$\mathrm{so},\:\mathrm{in}\:\mathrm{general}\:\mathrm{A}{B}\neq{BA} \\ $$$${But}\:{it}\:{not}\:{necessary}\:{mean}\:{that}\:{there}\:{no}\:{values} \\ $$$${such}\:{AB}={BA},\:{for}\:{squares}\:{matrizes} \\ $$$${IA}={AI} \\ $$$${where}\:{I}\:{is}\:{indenty}\:{matriz} \\ $$
Commented by maxmathsup by imad last updated on 05/Aug/18
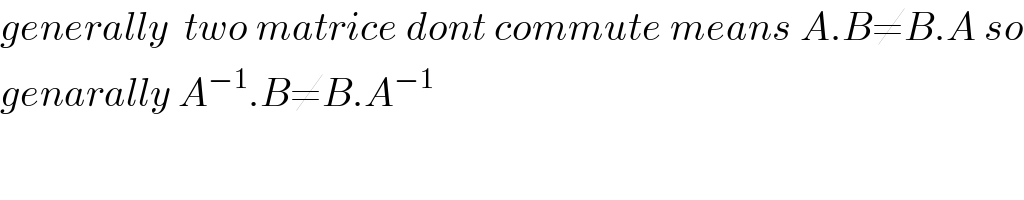
$${generally}\:\:{two}\:{matrice}\:{dont}\:{commute}\:{means}\:{A}.{B}\neq{B}.{A}\:{so} \\ $$$${genarally}\:{A}^{−\mathrm{1}} .{B}\neq{B}.{A}^{−\mathrm{1}} \\ $$
Answered by candre last updated on 05/Aug/18
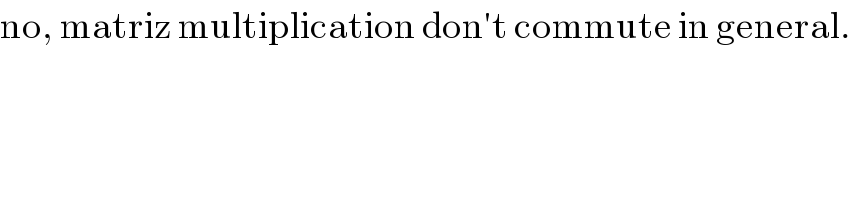
$$\mathrm{no},\:\mathrm{matriz}\:\mathrm{multiplication}\:\mathrm{don}'\mathrm{t}\:\mathrm{commute}\:\mathrm{in}\:\mathrm{general}. \\ $$
Commented by rahul 19 last updated on 05/Aug/18

$$\mathrm{ok}\:\mathrm{sir}. \\ $$
