
Question Number 176365 by Shrinava last updated on 16/Sep/22

$$\mathrm{In}\:\:\bigtriangleup\mathrm{ABC}\:\:\mathrm{the}\:\mathrm{following}\:\mathrm{relationship}\:\mathrm{holds}: \\ $$$$\underset{\boldsymbol{\mathrm{cyc}}} {\sum}\:\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{b}^{\mathrm{2}} \:+\:\mathrm{c}^{\mathrm{2}} }\:+\:\mathrm{4}\:\underset{\boldsymbol{\mathrm{cyc}}} {\prod}\:\mathrm{cos}\:\mathrm{A}\:\leqslant\:\mathrm{2} \\ $$
Answered by behi834171 last updated on 17/Sep/22
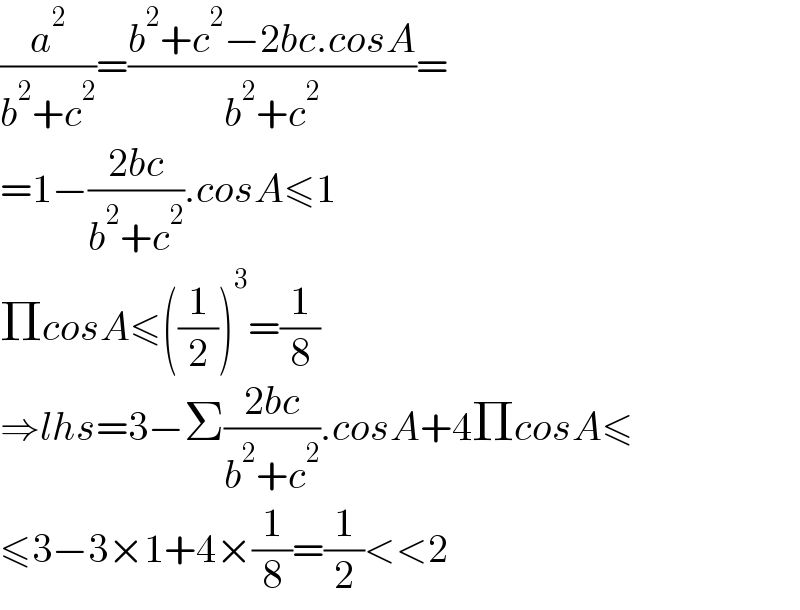
$$\frac{{a}^{\mathrm{2}} }{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }=\frac{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −\mathrm{2}{bc}.{cosA}}{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }= \\ $$$$=\mathrm{1}−\frac{\mathrm{2}{bc}}{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }.{cosA}\leqslant\mathrm{1} \\ $$$$\Pi{cosA}\leqslant\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{8}} \\ $$$$\Rightarrow{lhs}=\mathrm{3}−\Sigma\frac{\mathrm{2}{bc}}{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }.{cosA}+\mathrm{4}\Pi{cosA}\leqslant \\ $$$$\leqslant\mathrm{3}−\mathrm{3}×\mathrm{1}+\mathrm{4}×\frac{\mathrm{1}}{\mathrm{8}}=\frac{\mathrm{1}}{\mathrm{2}}<<\mathrm{2} \\ $$
Commented by Shrinava last updated on 18/Sep/22
$$\mathrm{cool}\:\mathrm{dera}\:\mathrm{professor}\:\mathrm{thank}\:\mathrm{you} \\ $$
