
Question Number 215769 by momoga last updated on 17/Jan/25

In △ABC, it is given that AC⊥CB, CD⊥AB, and CD = 12, AC = BC + 5. Please solve for the value of BC using a purely geometric method.
Commented by momoga last updated on 17/Jan/25
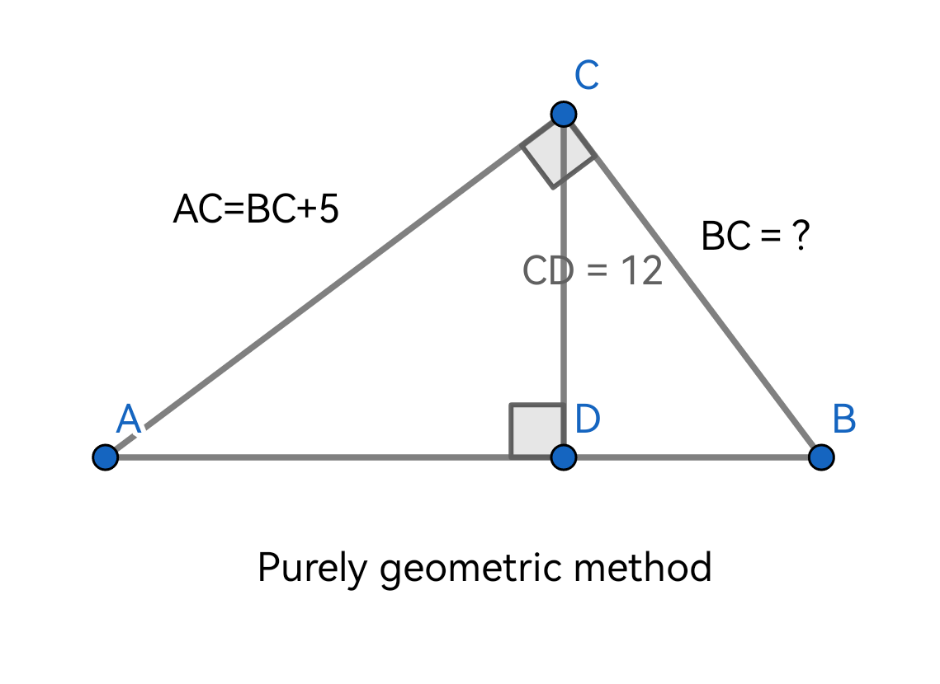
Answered by A5T last updated on 17/Jan/25
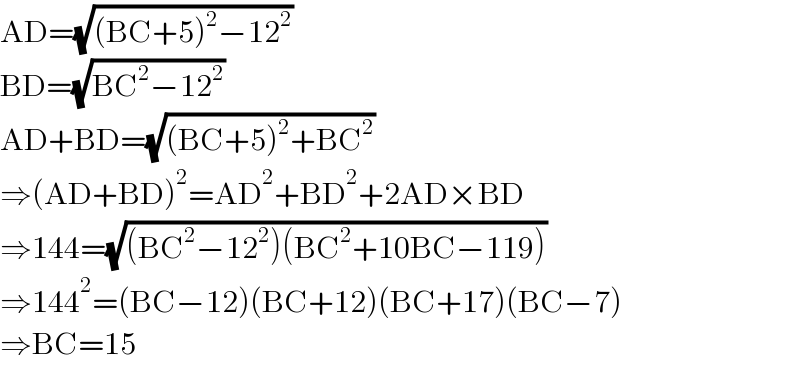
$$\mathrm{AD}=\sqrt{\left(\mathrm{BC}+\mathrm{5}\right)^{\mathrm{2}} −\mathrm{12}^{\mathrm{2}} } \\ $$$$\mathrm{BD}=\sqrt{\mathrm{BC}^{\mathrm{2}} −\mathrm{12}^{\mathrm{2}} } \\ $$$$\mathrm{AD}+\mathrm{BD}=\sqrt{\left(\mathrm{BC}+\mathrm{5}\right)^{\mathrm{2}} +\mathrm{BC}^{\mathrm{2}} } \\ $$$$\Rightarrow\left(\mathrm{AD}+\mathrm{BD}\right)^{\mathrm{2}} =\mathrm{AD}^{\mathrm{2}} +\mathrm{BD}^{\mathrm{2}} +\mathrm{2AD}×\mathrm{BD} \\ $$$$\Rightarrow\mathrm{144}=\sqrt{\left(\mathrm{BC}^{\mathrm{2}} −\mathrm{12}^{\mathrm{2}} \right)\left(\mathrm{BC}^{\mathrm{2}} +\mathrm{10BC}−\mathrm{119}\right)} \\ $$$$\Rightarrow\mathrm{144}^{\mathrm{2}} =\left(\mathrm{BC}−\mathrm{12}\right)\left(\mathrm{BC}+\mathrm{12}\right)\left(\mathrm{BC}+\mathrm{17}\right)\left(\mathrm{BC}−\mathrm{7}\right) \\ $$$$\Rightarrow\mathrm{BC}=\mathrm{15} \\ $$
Commented by momoga last updated on 18/Jan/25

Oh, so that’s how it is
Commented by momoga last updated on 17/Jan/25

I believe this is an algebraic approach, involving solving a quartic equation. Is there a geometric method, perhaps?
Commented by AntonCWX last updated on 18/Jan/25

$${No}. \\ $$$${When}\:{we}\:{are}\:{solving}\:{this}\:{kind}\:{of}\:{problem}, \\ $$$${We}\:{apply}\:{concept}\:{from}\:{geometry}\:{and}\:{transform}\:{it}\:{into}\:{equations}. \\ $$
Commented by AntonCWX last updated on 18/Jan/25
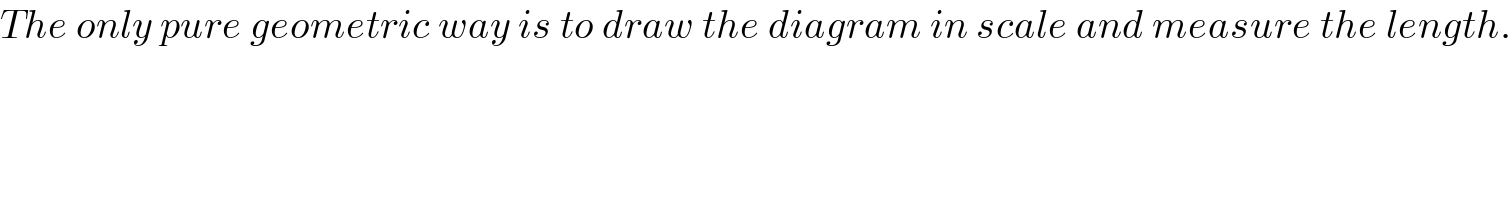
$${The}\:{only}\:{pure}\:{geometric}\:{way}\:{is}\:{to}\:{draw}\:{the}\:{diagram}\:{in}\:{scale}\:{and}\:{measure}\:{the}\:{length}. \\ $$
