
Question Number 174464 by Shrinava last updated on 01/Aug/22
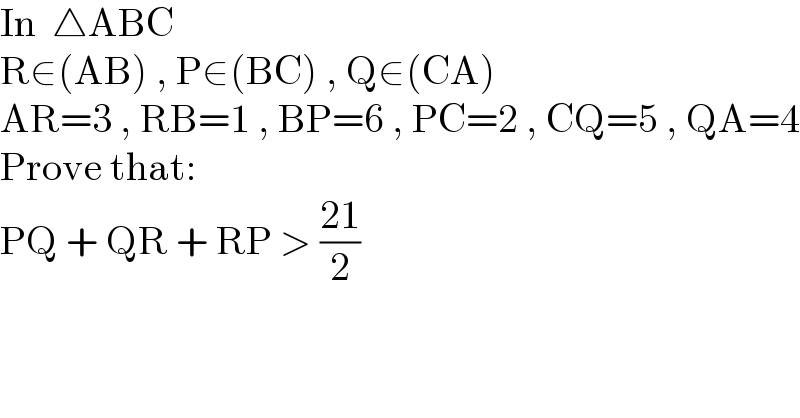
$$\mathrm{In}\:\:\bigtriangleup\mathrm{ABC} \\ $$$$\mathrm{R}\in\left(\mathrm{AB}\right)\:,\:\mathrm{P}\in\left(\mathrm{BC}\right)\:,\:\mathrm{Q}\in\left(\mathrm{CA}\right) \\ $$$$\mathrm{AR}=\mathrm{3}\:,\:\mathrm{RB}=\mathrm{1}\:,\:\mathrm{BP}=\mathrm{6}\:,\:\mathrm{PC}=\mathrm{2}\:,\:\mathrm{CQ}=\mathrm{5}\:,\:\mathrm{QA}=\mathrm{4} \\ $$$$\mathrm{Prove}\:\mathrm{that}: \\ $$$$\mathrm{PQ}\:+\:\mathrm{QR}\:+\:\mathrm{RP}\:>\:\frac{\mathrm{21}}{\mathrm{2}} \\ $$
