Question and Answers Forum

All Questions      Topic List

Geometry Questions

Previous in All Question      Next in All Question      

Previous in Geometry      Next in Geometry      

Question Number 207980 by mnjuly1970 last updated on 01/Jun/24

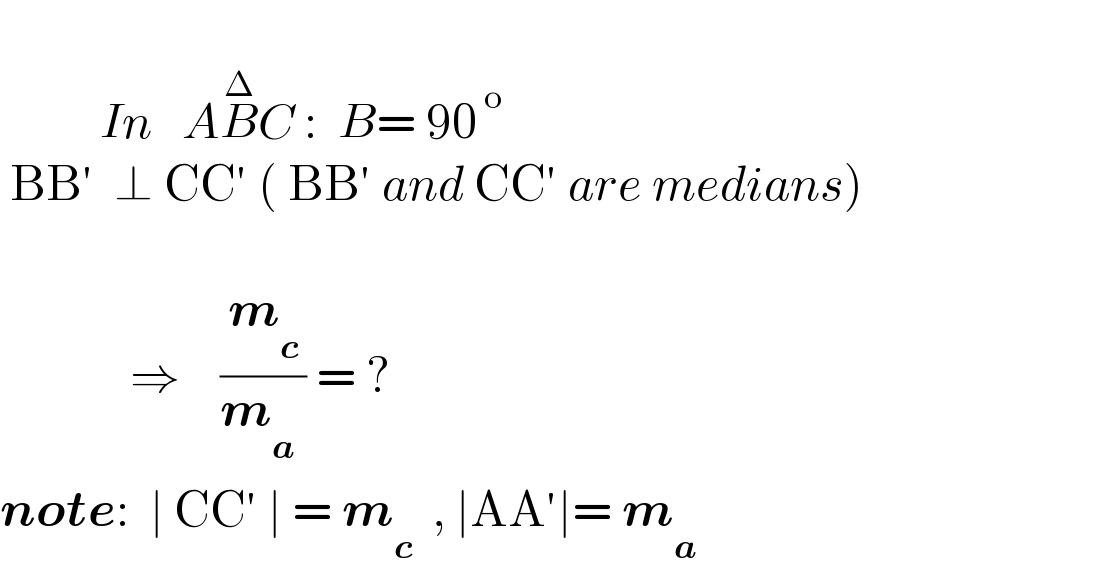
In AB^Δ C : B= 90^( o) BB′ ⊥ CC′ ( BB′ and CC′ are medians) ⇒ (m_c /(m_a )) = ? note: ∣ CC′ ∣ = m_c , ∣AA′∣= m_a

$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:{In}\:\:\:{A}\overset{\Delta} {{B}C}\::\:\:{B}=\:\mathrm{90}^{\:\mathrm{o}} \: \\ $$$$\:\mathrm{BB}'\:\:\bot\:\mathrm{CC}'\:\left(\:\mathrm{BB}'\:{and}\:\mathrm{CC}'\:{are}\:{medians}\right) \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:\:\:\:\frac{\boldsymbol{{m}}_{\boldsymbol{{c}}} }{\boldsymbol{{m}}_{\boldsymbol{{a}}} \:}\:=\:? \\ $$$$\boldsymbol{{note}}:\:\:\mid\:\mathrm{CC}'\:\mid\:=\:\boldsymbol{{m}}_{\boldsymbol{{c}}} \:\:,\:\mid\mathrm{AA}'\mid=\:\boldsymbol{{m}}_{\boldsymbol{{a}}} \\ $$

Answered by mr W last updated on 02/Jun/24

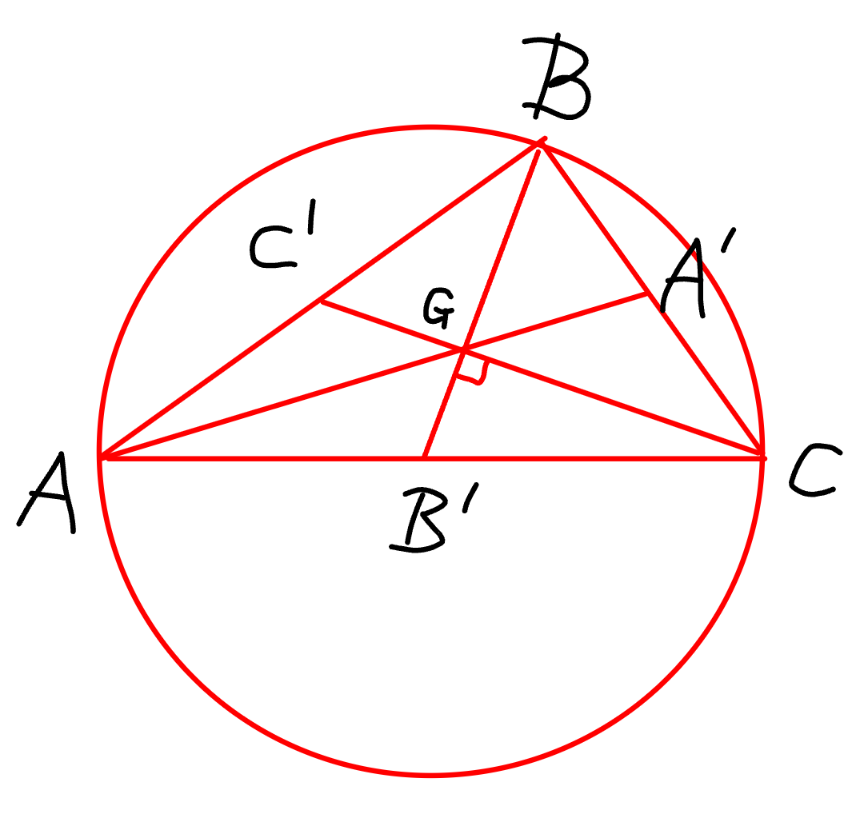
Commented by mr W last updated on 02/Jun/24

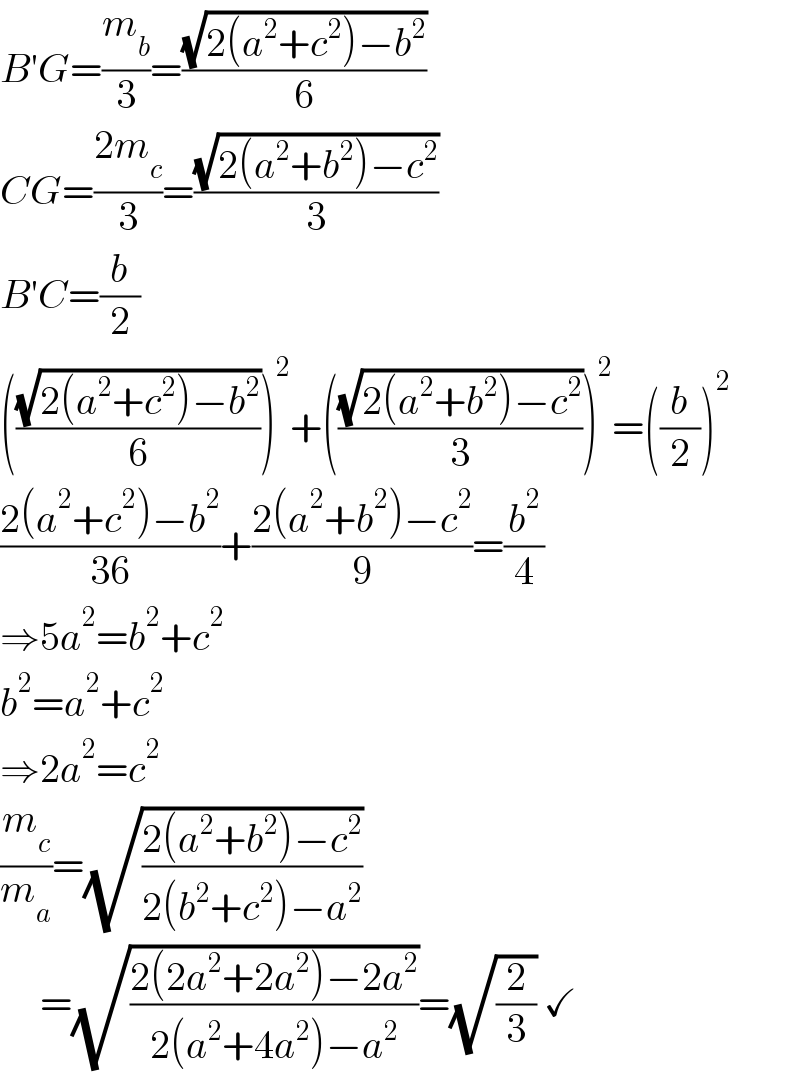
B′G=(m_b /3)=((√(2(a^2 +c^2 )−b^2 ))/6) CG=((2m_c )/3)=((√(2(a^2 +b^2 )−c^2 ))/3) B′C=(b/2) (((√(2(a^2 +c^2 )−b^2 ))/6))^2 +(((√(2(a^2 +b^2 )−c^2 ))/3))^2 =((b/2))^2 ((2(a^2 +c^2 )−b^2 )/(36))+((2(a^2 +b^2 )−c^2 )/9)=(b^2 /4) ⇒5a^2 =b^2 +c^2 b^2 =a^2 +c^2 ⇒2a^2 =c^2 (m_c /m_a )=(√((2(a^2 +b^2 )−c^2 )/(2(b^2 +c^2 )−a^2 ))) =(√((2(2a^2 +2a^2 )−2a^2 )/(2(a^2 +4a^2 )−a^2 )))=(√(2/3)) ✓

$${B}'{G}=\frac{{m}_{{b}} }{\mathrm{3}}=\frac{\sqrt{\mathrm{2}\left({a}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)−{b}^{\mathrm{2}} }}{\mathrm{6}} \\ $$$${CG}=\frac{\mathrm{2}{m}_{{c}} }{\mathrm{3}}=\frac{\sqrt{\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)−{c}^{\mathrm{2}} }}{\mathrm{3}} \\ $$$${B}'{C}=\frac{{b}}{\mathrm{2}} \\ $$$$\left(\frac{\sqrt{\mathrm{2}\left({a}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)−{b}^{\mathrm{2}} }}{\mathrm{6}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)−{c}^{\mathrm{2}} }}{\mathrm{3}}\right)^{\mathrm{2}} =\left(\frac{{b}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$\frac{\mathrm{2}\left({a}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)−{b}^{\mathrm{2}} }{\mathrm{36}}+\frac{\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)−{c}^{\mathrm{2}} }{\mathrm{9}}=\frac{{b}^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\Rightarrow\mathrm{5}{a}^{\mathrm{2}} ={b}^{\mathrm{2}} +{c}^{\mathrm{2}} \\ $$$${b}^{\mathrm{2}} ={a}^{\mathrm{2}} +{c}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{2}{a}^{\mathrm{2}} ={c}^{\mathrm{2}} \\ $$$$\frac{{m}_{{c}} }{{m}_{{a}} }=\sqrt{\frac{\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)−{c}^{\mathrm{2}} }{\mathrm{2}\left({b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)−{a}^{\mathrm{2}} }} \\ $$$$\:\:\:\:\:=\sqrt{\frac{\mathrm{2}\left(\mathrm{2}{a}^{\mathrm{2}} +\mathrm{2}{a}^{\mathrm{2}} \right)−\mathrm{2}{a}^{\mathrm{2}} }{\mathrm{2}\left({a}^{\mathrm{2}} +\mathrm{4}{a}^{\mathrm{2}} \right)−{a}^{\mathrm{2}} }}=\sqrt{\frac{\mathrm{2}}{\mathrm{3}}}\:\checkmark \\ $$

Commented by efronzo1 last updated on 02/Jun/24

AC is

$$\mathrm{AC}\:\mathrm{is}\:\:\cancel{\underbrace{\:}} \\ $$

Commented by mr W last updated on 02/Jun/24

yes, since ∠B=90°

$${yes},\:{since}\:\angle{B}=\mathrm{90}° \\ $$

Commented by mr W last updated on 02/Jun/24

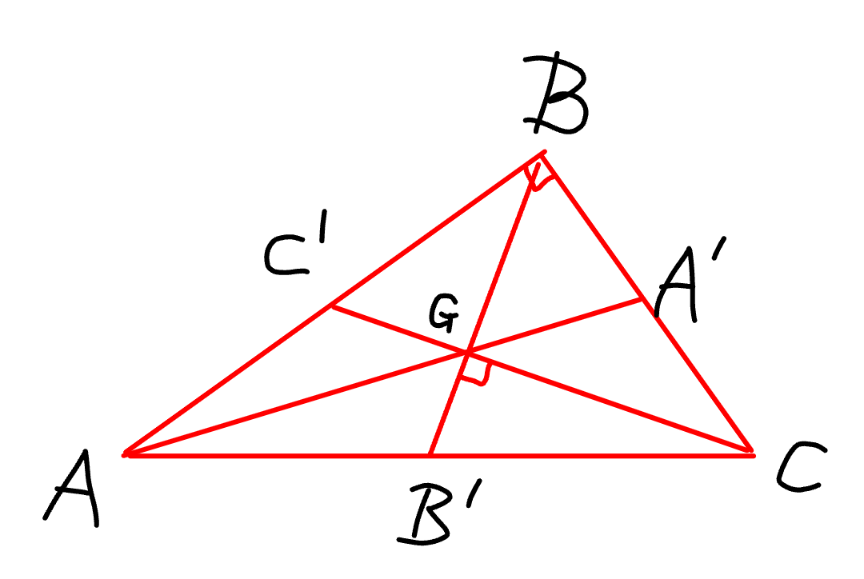
Commented by mnjuly1970 last updated on 02/Jun/24

grateful master very nice as always. ⋛

$${grateful}\:\:{master}\: \\ $$$${very}\:{nice}\:{as}\:{always}.\:\underline{\underbrace{\lesseqgtr}} \\ $$

Commented by Tawa11 last updated on 21/Jun/24

Weldone sir

$$\mathrm{Weldone}\:\mathrm{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com