
Question Number 32002 by rahul 19 last updated on 18/Mar/18
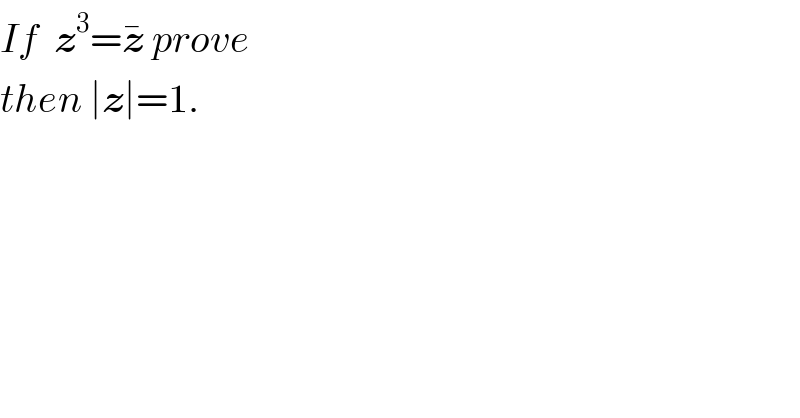
$${If}\:\:\boldsymbol{{z}}^{\mathrm{3}} =\bar {\boldsymbol{{z}}}\:{prove}\: \\ $$$${then}\:\mid\boldsymbol{{z}}\mid=\mathrm{1}. \\ $$
Answered by Tinkutara last updated on 18/Mar/18

$${z}^{\mathrm{3}} =\bar {{z}} \\ $$$$\mid{z}^{\mathrm{3}} \mid=\mid\bar {{z}}\mid \\ $$$$\mid{z}\mid^{\mathrm{3}} =\mid{z}\mid \\ $$$$\mid{z}\mid^{\mathrm{2}} =\mathrm{1} \\ $$$$\mid{z}\mid=\mathrm{1} \\ $$
Commented by Tinkutara last updated on 18/Mar/18
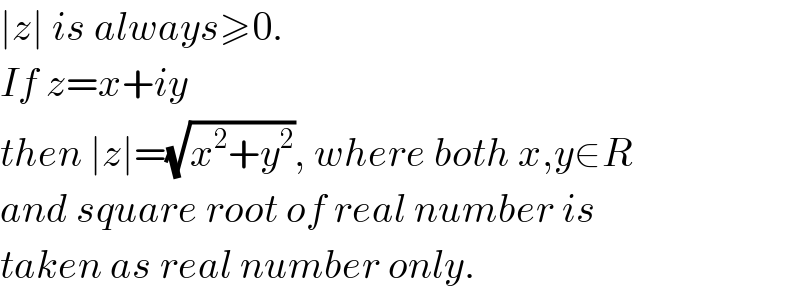
$$\mid{z}\mid\:{is}\:{always}\geqslant\mathrm{0}. \\ $$$${If}\:{z}={x}+{iy} \\ $$$${then}\:\mid{z}\mid=\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} },\:{where}\:{both}\:{x},{y}\in{R} \\ $$$${and}\:{square}\:{root}\:{of}\:{real}\:{number}\:{is} \\ $$$${taken}\:{as}\:{real}\:{number}\:{only}. \\ $$
Commented by rahul 19 last updated on 18/Mar/18

$${thanku}! \\ $$
