
Question Number 111850 by bemath last updated on 05/Sep/20
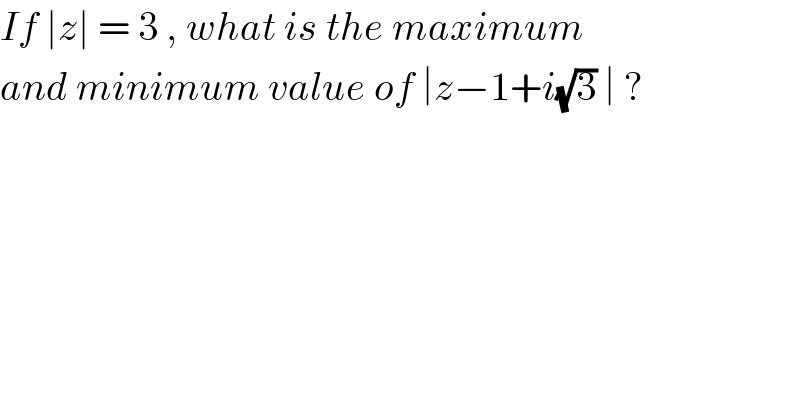
$${If}\:\mid{z}\mid\:=\:\mathrm{3}\:,\:{what}\:{is}\:{the}\:{maximum} \\ $$$${and}\:{minimum}\:{value}\:{of}\:\mid{z}−\mathrm{1}+{i}\sqrt{\mathrm{3}}\:\mid\:? \\ $$
Answered by ajfour last updated on 05/Sep/20

$${max}\mid{z}−\mathrm{1}+{i}\sqrt{\mathrm{3}}\mid=\mathrm{5} \\ $$$${min}\mid{z}−\mathrm{1}+{i}\sqrt{\mathrm{3}}\mid=\mathrm{1} \\ $$
Commented by ajfour last updated on 05/Sep/20
Answered by Her_Majesty last updated on 05/Sep/20
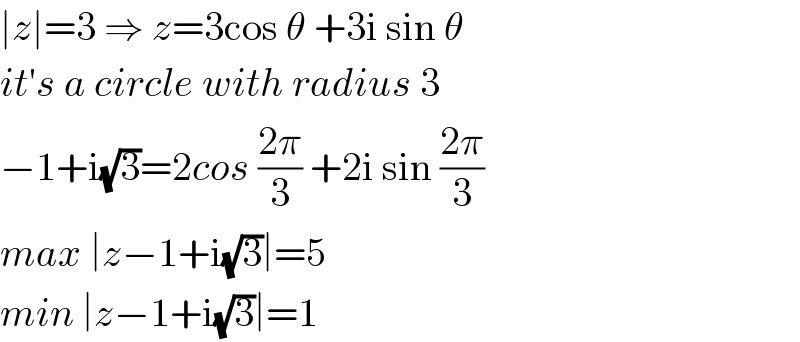
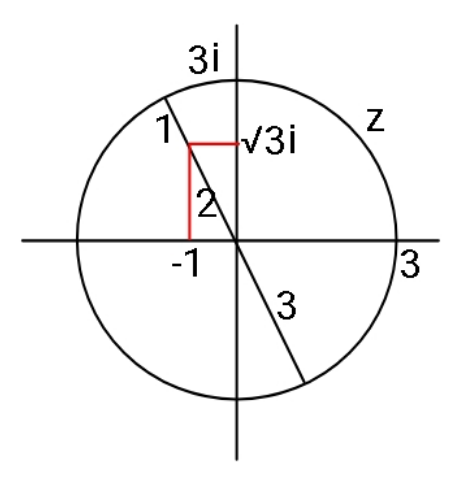
$$\mid{z}\mid=\mathrm{3}\:\Rightarrow\:{z}=\mathrm{3cos}\:\theta\:+\mathrm{3i}\:\mathrm{sin}\:\theta \\ $$$${it}'{s}\:{a}\:{circle}\:{with}\:{radius}\:\mathrm{3} \\ $$$$−\mathrm{1}+\mathrm{i}\sqrt{\mathrm{3}}=\mathrm{2}{cos}\:\frac{\mathrm{2}\pi}{\mathrm{3}}\:+\mathrm{2i}\:\mathrm{sin}\:\frac{\mathrm{2}\pi}{\mathrm{3}} \\ $$$${max}\:\mid{z}−\mathrm{1}+\mathrm{i}\sqrt{\mathrm{3}}\mid=\mathrm{5} \\ $$$${min}\:\mid{z}−\mathrm{1}+\mathrm{i}\sqrt{\mathrm{3}}\mid=\mathrm{1} \\ $$
Answered by bemath last updated on 05/Sep/20
$${great}\:{santuy}\:\:{both}\:.... \\ $$
Answered by 1549442205PVT last updated on 05/Sep/20
)) =(√(16.9))=12 ⇒−12≤2b(√3)−2a≤12 (3) From (2)and (3) we get 1≤Q≤25⇔1≤P≤5 P=1⇔Q=1⇔ { ((a=3/2)),((b=−3(√3)/2)) :} P=5⇔Q=25⇔ { ((a=−3/2)),((b=3(√3)/2)) :} Thus,P=∣z−1+i(√3) ∣ has the smallest value equal to 1 when (a,b)=((3/2),((−3(√3))/2)) i.e when z=(3/2)−((3i(√3))/2) and the greatest value equal to 5 when (a,b)=(((−3)/2),((3(√3))/2)) i.e z=((−3)/2)+((3i(√3))/2)](Q111905.png)
$$\mathrm{Put}\:\mathrm{z}=\mathrm{a}+\mathrm{bi}\Rightarrow\mathrm{z}−\mathrm{1}+\mathrm{i}\sqrt{\mathrm{3}}=\left(\mathrm{a}−\mathrm{1}\right)+\mathrm{i}\left(\mathrm{b}+\sqrt{\mathrm{3}}\right) \\ $$$$\mid\mathrm{z}\mid=\mathrm{3}\Leftrightarrow\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} }\:=\mathrm{3}\Leftrightarrow\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} =\mathrm{9}\left(\mathrm{1}\right) \\ $$$$\mid\mathrm{z}−\mathrm{1}+\mathrm{i}\sqrt{\mathrm{3}}\mid=\sqrt{\left(\mathrm{a}−\mathrm{1}\right)^{\mathrm{2}} +\left(\mathrm{b}+\sqrt{\mathrm{3}}\right)^{\mathrm{2}} } \\ $$$$\mathrm{We}\:\mathrm{need}\:\mathrm{find}\:\mathrm{least}\:\mathrm{and}\:\mathrm{greaest}\:\mathrm{value} \\ $$$$\mathrm{of}\:\mathrm{the}\:\mathrm{expression}\: \\ $$$$\mathrm{P}=\sqrt{\left(\mathrm{a}−\mathrm{1}\right)^{\mathrm{2}} +\left(\mathrm{b}+\sqrt{\mathrm{3}}\right)^{\mathrm{2}} }\:\mathrm{which}\:\mathrm{is}\: \\ $$$$\mathrm{equivalent}\:\mathrm{to}\:\mathrm{find}\:\mathrm{least}\:\mathrm{and}\:\mathrm{greaest} \\ $$$$\mathrm{value}\:\mathrm{of}\:\:\mathrm{Q}=\left(\mathrm{a}−\mathrm{1}\right)^{\mathrm{2}} +\left(\mathrm{b}+\sqrt{\mathrm{3}}\right)^{\mathrm{2}} \\ $$$$=\mathrm{13}+\mathrm{2}\boldsymbol{\mathrm{b}}\sqrt{\mathrm{3}}−\boldsymbol{\mathrm{a}}\left(\mathrm{2}\right) \\ $$$$\mathrm{Apply}\:\mathrm{the}\:\mathrm{inequality}\:\mid\mathrm{ax}+\mathrm{by}\mid\leqslant \\ $$$$\sqrt{\left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} \right)\left(\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \right)}\:\mathrm{we}\:\mathrm{have} \\ $$$$\mid\mathrm{2b}\sqrt{\mathrm{3}}−\mathrm{a}\mid=\mid\left(\mathrm{2}\sqrt{\mathrm{3}}\right).\mathrm{b}+\left(−\mathrm{2}\right).\mathrm{a}\mid\leqslant \\ $$$$\sqrt{\left[\left(\mathrm{2}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} +\left(−\mathrm{2}\right)^{\mathrm{2}} \right]\left(\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} \right)}\:=\sqrt{\mathrm{16}.\mathrm{9}}=\mathrm{12} \\ $$$$\Rightarrow−\mathrm{12}\leqslant\mathrm{2b}\sqrt{\mathrm{3}}−\mathrm{2a}\leqslant\mathrm{12}\:\:\:\left(\mathrm{3}\right) \\ $$$$\mathrm{From}\:\left(\mathrm{2}\right)\mathrm{and}\:\left(\mathrm{3}\right)\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{1}\leqslant\mathrm{Q}\leqslant\mathrm{25}\Leftrightarrow\mathrm{1}\leqslant\mathrm{P}\leqslant\mathrm{5} \\ $$$$\mathrm{P}=\mathrm{1}\Leftrightarrow\mathrm{Q}=\mathrm{1}\Leftrightarrow\begin{cases}{\mathrm{a}=\mathrm{3}/\mathrm{2}}\\{\mathrm{b}=−\mathrm{3}\sqrt{\mathrm{3}}/\mathrm{2}}\end{cases} \\ $$$$\mathrm{P}=\mathrm{5}\Leftrightarrow\mathrm{Q}=\mathrm{25}\Leftrightarrow\begin{cases}{\mathrm{a}=−\mathrm{3}/\mathrm{2}}\\{\mathrm{b}=\mathrm{3}\sqrt{\mathrm{3}}/\mathrm{2}}\end{cases} \\ $$$$\mathrm{Thus},\mathrm{P}=\mid\mathrm{z}−\mathrm{1}+\mathrm{i}\sqrt{\mathrm{3}}\:\mid\:\:\:\mathrm{has}\:\mathrm{the}\:\mathrm{smallest} \\ $$$$\boldsymbol{\mathrm{value}}\:\boldsymbol{\mathrm{equal}}\:\boldsymbol{\mathrm{to}}\:\mathrm{1}\:\boldsymbol{\mathrm{when}}\:\left(\boldsymbol{\mathrm{a}},\boldsymbol{\mathrm{b}}\right)=\left(\frac{\mathrm{3}}{\mathrm{2}},\frac{−\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}}\right) \\ $$$$\mathrm{i}.\mathrm{e}\:\mathrm{when}\:\mathrm{z}=\frac{\mathrm{3}}{\mathrm{2}}−\frac{\mathrm{3i}\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\boldsymbol{\mathrm{and}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{greatest}}\:\boldsymbol{\mathrm{value}}\:\boldsymbol{\mathrm{equal}}\:\boldsymbol{\mathrm{to}}\:\mathrm{5} \\ $$$$\mathrm{when}\:\left(\mathrm{a},\mathrm{b}\right)=\left(\frac{−\mathrm{3}}{\mathrm{2}},\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}}\right)\:\mathrm{i}.\mathrm{e}\:\mathrm{z}=\frac{−\mathrm{3}}{\mathrm{2}}+\frac{\mathrm{3i}\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$
