
Question Number 19735 by Tinkutara last updated on 15/Aug/17
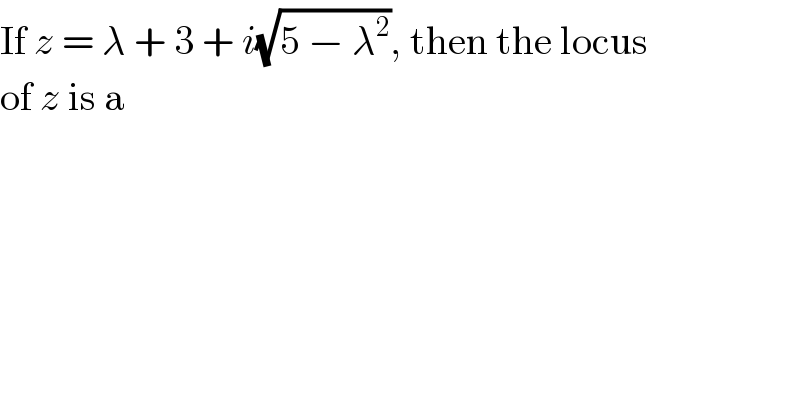
$$\mathrm{If}\:{z}\:=\:\lambda\:+\:\mathrm{3}\:+\:{i}\sqrt{\mathrm{5}\:−\:\lambda^{\mathrm{2}} },\:\mathrm{then}\:\mathrm{the}\:\mathrm{locus} \\ $$$$\mathrm{of}\:{z}\:\mathrm{is}\:\mathrm{a} \\ $$
Answered by ajfour last updated on 15/Aug/17
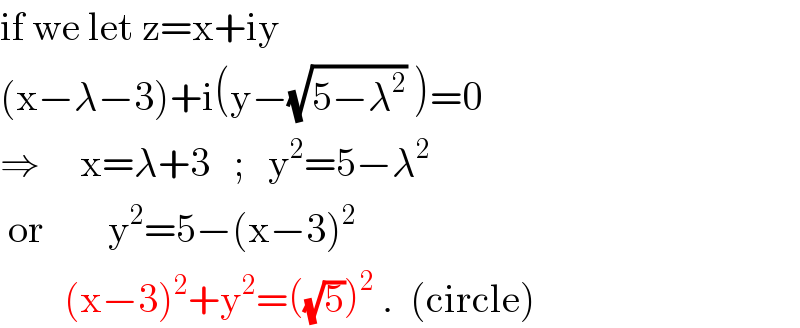
$$\mathrm{if}\:\mathrm{we}\:\mathrm{let}\:\mathrm{z}=\mathrm{x}+\mathrm{iy} \\ $$$$\left(\mathrm{x}−\lambda−\mathrm{3}\right)+\mathrm{i}\left(\mathrm{y}−\sqrt{\mathrm{5}−\lambda^{\mathrm{2}} }\:\right)=\mathrm{0} \\ $$$$\Rightarrow\:\:\:\:\:\mathrm{x}=\lambda+\mathrm{3}\:\:\:;\:\:\:\mathrm{y}^{\mathrm{2}} =\mathrm{5}−\lambda^{\mathrm{2}} \\ $$$$\:\mathrm{or}\:\:\:\:\:\:\:\:\mathrm{y}^{\mathrm{2}} =\mathrm{5}−\left(\mathrm{x}−\mathrm{3}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\left(\mathrm{x}−\mathrm{3}\right)^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} =\left(\sqrt{\mathrm{5}}\right)^{\mathrm{2}} \:.\:\:\left(\mathrm{circle}\right) \\ $$
Commented by Tinkutara last updated on 15/Aug/17
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$
