Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 140443 by EnterUsername last updated on 07/May/21

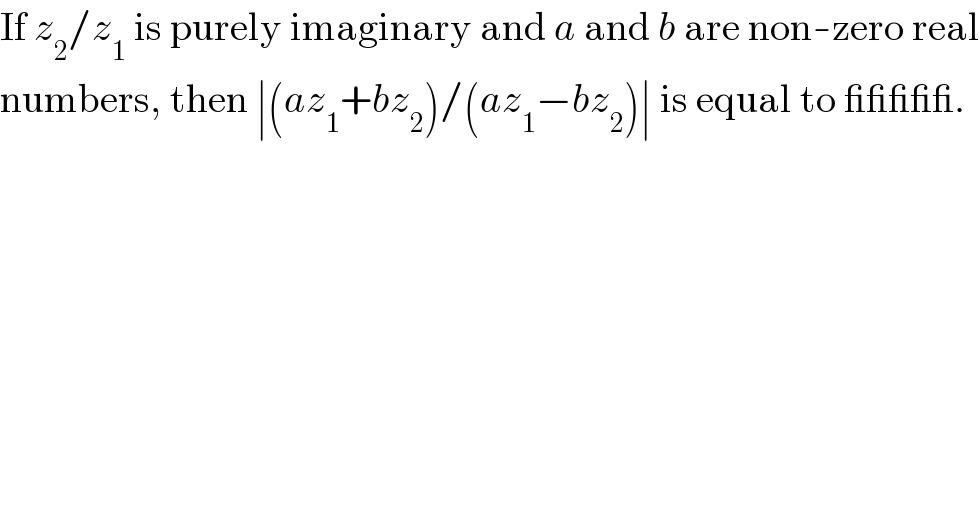
If z_2 /z_1 is purely imaginary and a and b are non-zero real numbers, then ∣(az_1 +bz_2 )/(az_1 −bz_2 )∣ is equal to _____.

$$\mathrm{If}\:{z}_{\mathrm{2}} /{z}_{\mathrm{1}} \:\mathrm{is}\:\mathrm{purely}\:\mathrm{imaginary}\:\mathrm{and}\:{a}\:\mathrm{and}\:{b}\:\mathrm{are}\:\mathrm{non}-\mathrm{zero}\:\mathrm{real} \\ $$$$\mathrm{numbers},\:\mathrm{then}\:\mid\left({az}_{\mathrm{1}} +{bz}_{\mathrm{2}} \right)/\left({az}_{\mathrm{1}} −{bz}_{\mathrm{2}} \right)\mid\:\mathrm{is}\:\mathrm{equal}\:\mathrm{to}\:\_\_\_\_\_. \\ $$

Answered by mr W last updated on 07/May/21

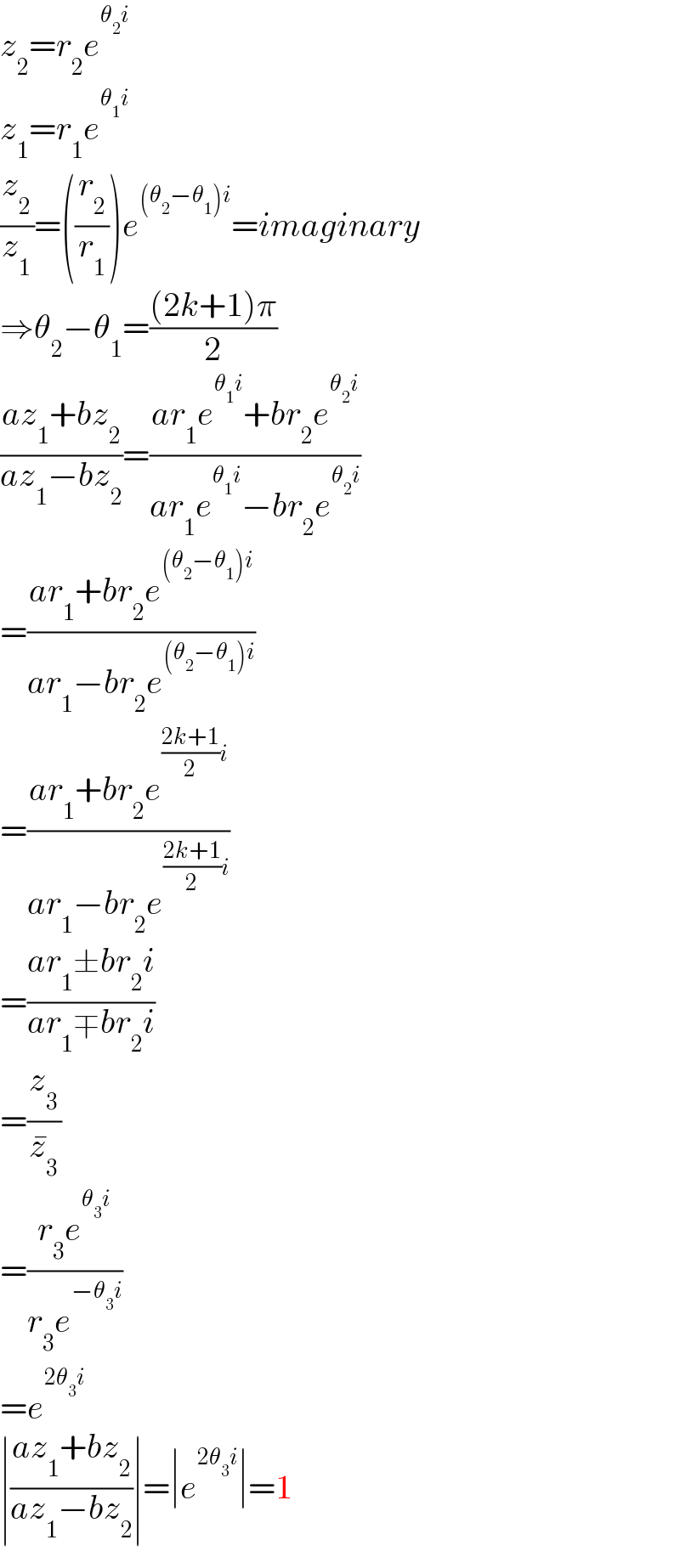
z_2 =r_2 e^(θ_2 i) z_1 =r_1 e^(θ_1 i) (z_2 /z_1 )=((r_2 /r_1 ))e^((θ_2 −θ_1 )i) =imaginary ⇒θ_2 −θ_1 =(((2k+1)π)/2) ((az_1 +bz_2 )/(az_1 −bz_2 ))=((ar_1 e^(θ_1 i) +br_2 e^(θ_2 i) )/(ar_1 e^(θ_1 i) −br_2 e^(θ_2 i) )) =((ar_1 +br_2 e^((θ_2 −θ_1 )i) )/(ar_1 −br_2 e^((θ_2 −θ_1 )i) )) =((ar_1 +br_2 e^(((2k+1)/2)i) )/(ar_1 −br_2 e^(((2k+1)/2)i) )) =((ar_1 ±br_2 i)/(ar_1 ∓br_2 i)) =(z_3 /z_3 ^� ) =((r_3 e^(θ_3 i) )/(r_3 e^(−θ_3 i) )) =e^(2θ_3 i) ∣((az_1 +bz_2 )/(az_1 −bz_2 ))∣=∣e^(2θ_3 i) ∣=1

$${z}_{\mathrm{2}} ={r}_{\mathrm{2}} {e}^{\theta_{\mathrm{2}} {i}} \\ $$$${z}_{\mathrm{1}} ={r}_{\mathrm{1}} {e}^{\theta_{\mathrm{1}} {i}} \\ $$$$\frac{{z}_{\mathrm{2}} }{{z}_{\mathrm{1}} }=\left(\frac{{r}_{\mathrm{2}} }{{r}_{\mathrm{1}} }\right){e}^{\left(\theta_{\mathrm{2}} −\theta_{\mathrm{1}} \right){i}} ={imaginary} \\ $$$$\Rightarrow\theta_{\mathrm{2}} −\theta_{\mathrm{1}} =\frac{\left(\mathrm{2}{k}+\mathrm{1}\right)\pi}{\mathrm{2}} \\ $$$$\frac{{az}_{\mathrm{1}} +{bz}_{\mathrm{2}} }{{az}_{\mathrm{1}} −{bz}_{\mathrm{2}} }=\frac{{ar}_{\mathrm{1}} {e}^{\theta_{\mathrm{1}} {i}} +{br}_{\mathrm{2}} {e}^{\theta_{\mathrm{2}} {i}} }{{ar}_{\mathrm{1}} {e}^{\theta_{\mathrm{1}} {i}} −{br}_{\mathrm{2}} {e}^{\theta_{\mathrm{2}} {i}} } \\ $$$$=\frac{{ar}_{\mathrm{1}} +{br}_{\mathrm{2}} {e}^{\left(\theta_{\mathrm{2}} −\theta_{\mathrm{1}} \right){i}} }{{ar}_{\mathrm{1}} −{br}_{\mathrm{2}} {e}^{\left(\theta_{\mathrm{2}} −\theta_{\mathrm{1}} \right){i}} } \\ $$$$=\frac{{ar}_{\mathrm{1}} +{br}_{\mathrm{2}} {e}^{\frac{\mathrm{2}{k}+\mathrm{1}}{\mathrm{2}}{i}} }{{ar}_{\mathrm{1}} −{br}_{\mathrm{2}} {e}^{\frac{\mathrm{2}{k}+\mathrm{1}}{\mathrm{2}}{i}} } \\ $$$$=\frac{{ar}_{\mathrm{1}} \pm{br}_{\mathrm{2}} {i}}{{ar}_{\mathrm{1}} \mp{br}_{\mathrm{2}} {i}} \\ $$$$=\frac{{z}_{\mathrm{3}} }{\bar {{z}}_{\mathrm{3}} } \\ $$$$=\frac{{r}_{\mathrm{3}} {e}^{\theta_{\mathrm{3}} {i}} }{{r}_{\mathrm{3}} {e}^{−\theta_{\mathrm{3}} {i}} } \\ $$$$={e}^{\mathrm{2}\theta_{\mathrm{3}} {i}} \\ $$$$\mid\frac{{az}_{\mathrm{1}} +{bz}_{\mathrm{2}} }{{az}_{\mathrm{1}} −{bz}_{\mathrm{2}} }\mid=\mid{e}^{\mathrm{2}\theta_{\mathrm{3}} {i}} \mid=\mathrm{1} \\ $$

Commented by EnterUsername last updated on 07/May/21

Thank you, Sir

$$\mathrm{Thank}\:\mathrm{you},\:\mathrm{Sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com