
Question Number 49174 by rahul 19 last updated on 04/Dec/18
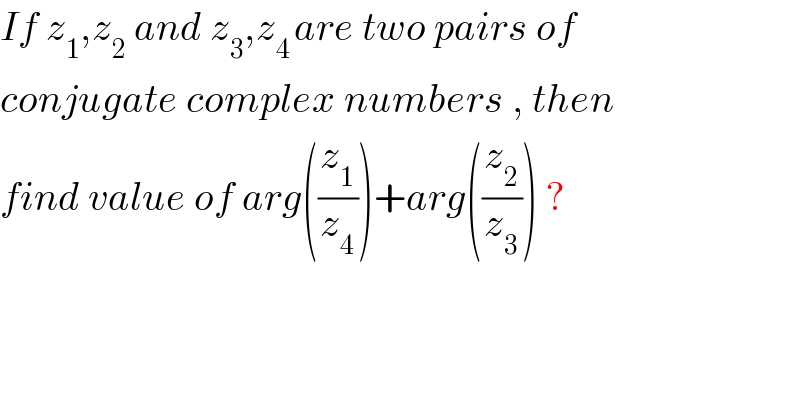
$${If}\:{z}_{\mathrm{1}} ,{z}_{\mathrm{2}} \:{and}\:{z}_{\mathrm{3}} ,{z}_{\mathrm{4}\:} {are}\:{two}\:{pairs}\:{of}\: \\ $$$${conjugate}\:{complex}\:{numbers}\:,\:{then}\: \\ $$$${find}\:{value}\:{of}\:{arg}\left(\frac{{z}_{\mathrm{1}} }{{z}_{\mathrm{4}} }\right)+{arg}\left(\frac{{z}_{\mathrm{2}} }{{z}_{\mathrm{3}} }\right)\:? \\ $$
Commented by rahul 19 last updated on 04/Dec/18
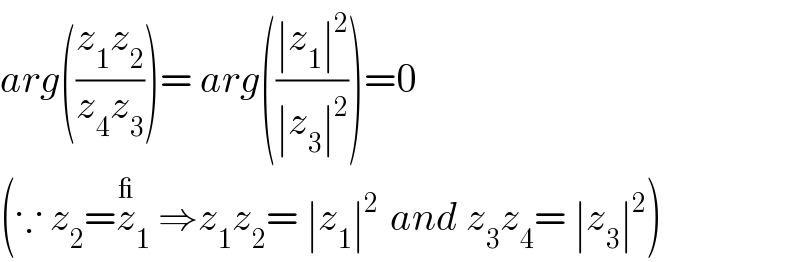
$${arg}\left(\frac{{z}_{\mathrm{1}} {z}_{\mathrm{2}} }{{z}_{\mathrm{4}} {z}_{\mathrm{3}} }\right)=\:{arg}\left(\frac{\mid{z}_{\mathrm{1}} \mid^{\mathrm{2}} }{\mid{z}_{\mathrm{3}} \mid^{\mathrm{2}} }\right)=\mathrm{0} \\ $$$$\left(\because\:{z}_{\mathrm{2}} =\overset{\_} {{z}}_{\mathrm{1}} \:\Rightarrow{z}_{\mathrm{1}} {z}_{\mathrm{2}} =\:\mid{z}_{\mathrm{1}} \mid^{\mathrm{2}\:} \:{and}\:{z}_{\mathrm{3}} {z}_{\mathrm{4}} =\:\mid{z}_{\mathrm{3}} \mid^{\mathrm{2}} \right) \\ $$
Answered by MJS last updated on 04/Dec/18
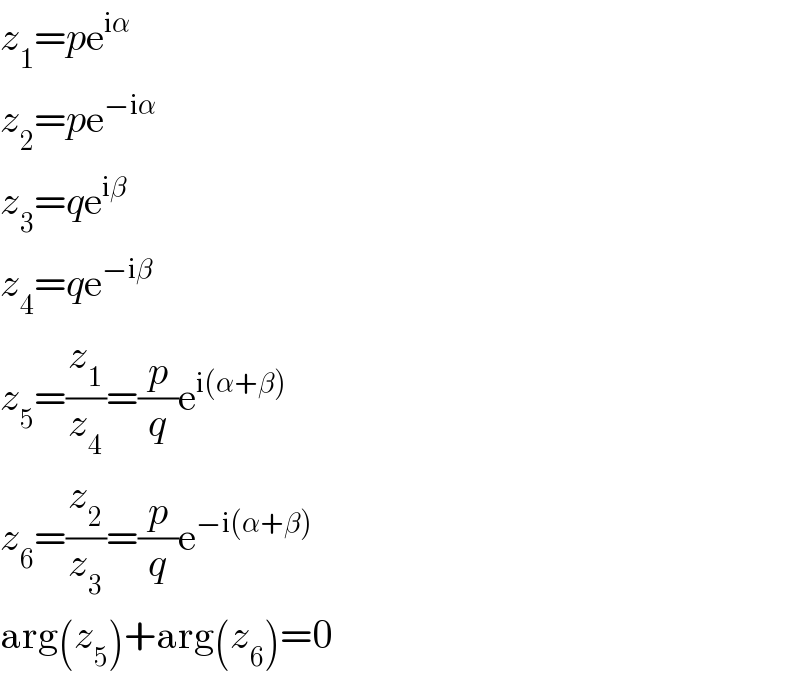
$${z}_{\mathrm{1}} ={p}\mathrm{e}^{\mathrm{i}\alpha} \\ $$$${z}_{\mathrm{2}} ={p}\mathrm{e}^{−\mathrm{i}\alpha} \\ $$$${z}_{\mathrm{3}} ={q}\mathrm{e}^{\mathrm{i}\beta} \\ $$$${z}_{\mathrm{4}} ={q}\mathrm{e}^{−\mathrm{i}\beta} \\ $$$${z}_{\mathrm{5}} =\frac{{z}_{\mathrm{1}} }{{z}_{\mathrm{4}} }=\frac{{p}}{{q}}\mathrm{e}^{\mathrm{i}\left(\alpha+\beta\right)} \\ $$$${z}_{\mathrm{6}} =\frac{{z}_{\mathrm{2}} }{{z}_{\mathrm{3}} }=\frac{{p}}{{q}}\mathrm{e}^{−\mathrm{i}\left(\alpha+\beta\right)} \\ $$$$\mathrm{arg}\left({z}_{\mathrm{5}} \right)+\mathrm{arg}\left({z}_{\mathrm{6}} \right)=\mathrm{0} \\ $$
Commented by rahul 19 last updated on 04/Dec/18
thank you sir!����
