Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 139838 by EnterUsername last updated on 01/May/21

If z_1 , z_2 and z_3 are the vertices of a right-angled isos- celes triangle described in counter clock sense and right angled at z_3 , then (z_1 −z_2 )^2 is equal to (A) (z_1 −z_3 )(z_3 −z_2 ) (B) 2(z_1 −z_3 )(z_3 −z_2 ) (C) 3(z_1 −z_3 )(z_3 −z_2 ) (D) 3(z_3 −z_1 )(z_3 −z_2 )

$$\mathrm{If}\:{z}_{\mathrm{1}} ,\:{z}_{\mathrm{2}} \:\mathrm{and}\:{z}_{\mathrm{3}} \:\mathrm{are}\:\mathrm{the}\:\mathrm{vertices}\:\mathrm{of}\:\mathrm{a}\:\mathrm{right}-\mathrm{angled}\:\mathrm{isos}- \\ $$$$\mathrm{celes}\:\mathrm{triangle}\:\mathrm{described}\:\mathrm{in}\:\mathrm{counter}\:\mathrm{clock}\:\mathrm{sense}\:\mathrm{and} \\ $$$$\mathrm{right}\:\mathrm{angled}\:\mathrm{at}\:{z}_{\mathrm{3}} ,\:\mathrm{then}\:\left({z}_{\mathrm{1}} −{z}_{\mathrm{2}} \right)^{\mathrm{2}} \:\mathrm{is}\:\mathrm{equal}\:\mathrm{to}\: \\ $$$$\left(\mathrm{A}\right)\:\left({z}_{\mathrm{1}} −{z}_{\mathrm{3}} \right)\left({z}_{\mathrm{3}} −{z}_{\mathrm{2}} \right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{B}\right)\:\mathrm{2}\left({z}_{\mathrm{1}} −{z}_{\mathrm{3}} \right)\left({z}_{\mathrm{3}} −{z}_{\mathrm{2}} \right) \\ $$$$\left(\mathrm{C}\right)\:\mathrm{3}\left({z}_{\mathrm{1}} −{z}_{\mathrm{3}} \right)\left({z}_{\mathrm{3}} −{z}_{\mathrm{2}} \right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{D}\right)\:\mathrm{3}\left({z}_{\mathrm{3}} −{z}_{\mathrm{1}} \right)\left({z}_{\mathrm{3}} −{z}_{\mathrm{2}} \right) \\ $$

Answered by mr W last updated on 02/May/21

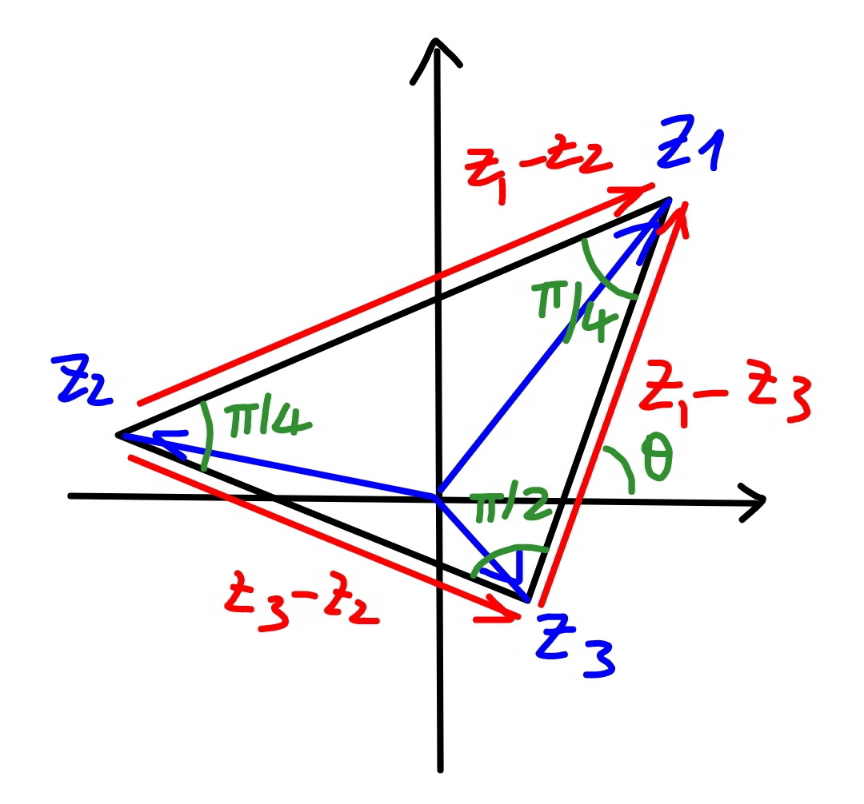
Commented by mr W last updated on 02/May/21

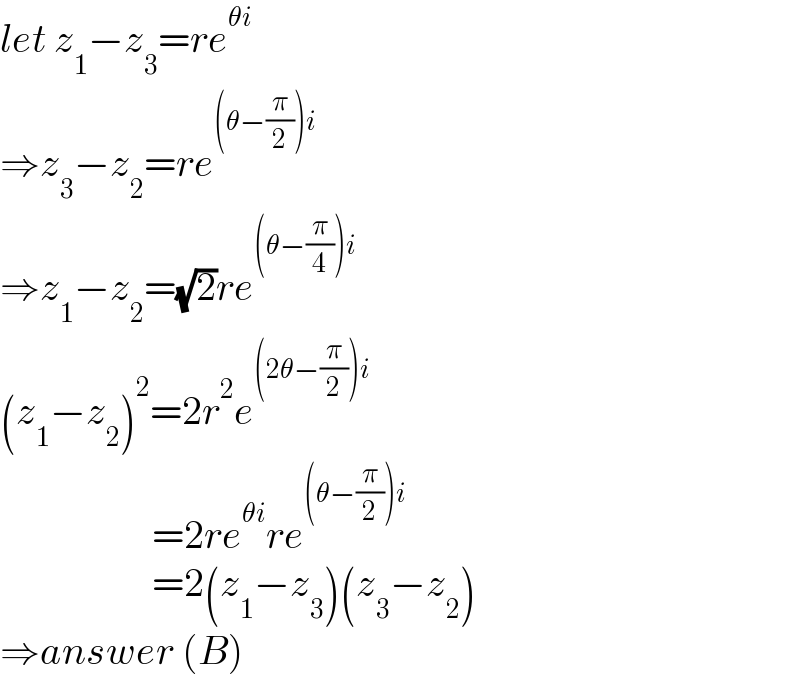
let z_1 −z_3 =re^(θi) ⇒z_3 −z_2 =re^((θ−(π/2))i) ⇒z_1 −z_2 =(√2)re^((θ−(π/4))i) (z_1 −z_2 )^2 =2r^2 e^((2θ−(π/2))i) =2re^(θi) re^((θ−(π/2))i) =2(z_1 −z_3 )(z_3 −z_2 ) ⇒answer (B)

$${let}\:{z}_{\mathrm{1}} −{z}_{\mathrm{3}} ={re}^{\theta{i}} \\ $$$$\Rightarrow{z}_{\mathrm{3}} −{z}_{\mathrm{2}} ={re}^{\left(\theta−\frac{\pi}{\mathrm{2}}\right){i}} \\ $$$$\Rightarrow{z}_{\mathrm{1}} −{z}_{\mathrm{2}} =\sqrt{\mathrm{2}}{re}^{\left(\theta−\frac{\pi}{\mathrm{4}}\right){i}} \\ $$$$\left({z}_{\mathrm{1}} −{z}_{\mathrm{2}} \right)^{\mathrm{2}} =\mathrm{2}{r}^{\mathrm{2}} {e}^{\left(\mathrm{2}\theta−\frac{\pi}{\mathrm{2}}\right){i}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}{re}^{\theta{i}} {re}^{\left(\theta−\frac{\pi}{\mathrm{2}}\right){i}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}\left({z}_{\mathrm{1}} −{z}_{\mathrm{3}} \right)\left({z}_{\mathrm{3}} −{z}_{\mathrm{2}} \right) \\ $$$$\Rightarrow{answer}\:\left({B}\right) \\ $$

Commented by EnterUsername last updated on 02/May/21

Thank You, Sir

$$\mathrm{Thank}\:\mathrm{You},\:\mathrm{Sir} \\ $$

Commented by EnterUsername last updated on 02/May/21

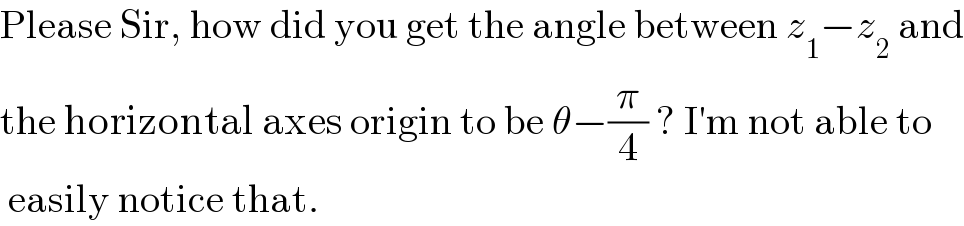
Please Sir, how did you get the angle between z_1 −z_2 and the horizontal axes origin to be θ−(π/4) ? I′m not able to easily notice that.

$$\mathrm{Please}\:\mathrm{Sir},\:\mathrm{how}\:\mathrm{did}\:\mathrm{you}\:\mathrm{get}\:\mathrm{the}\:\mathrm{angle}\:\mathrm{between}\:{z}_{\mathrm{1}} −{z}_{\mathrm{2}} \:\mathrm{and} \\ $$$$\mathrm{the}\:\mathrm{horizontal}\:\mathrm{axes}\:\mathrm{origin}\:\mathrm{to}\:\mathrm{be}\:\theta−\frac{\pi}{\mathrm{4}}\:?\:\mathrm{I}'\mathrm{m}\:\mathrm{not}\:\mathrm{able}\:\mathrm{to} \\ $$$$\:\mathrm{easily}\:\mathrm{notice}\:\mathrm{that}. \\ $$

Commented by mr W last updated on 02/May/21

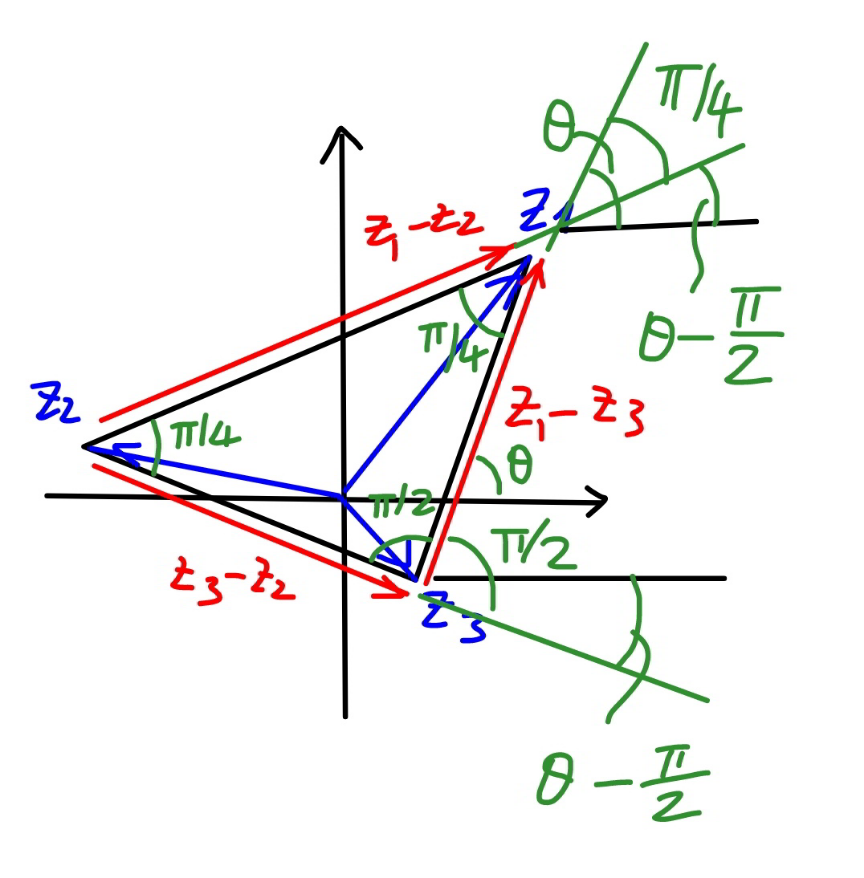
Commented by EnterUsername last updated on 02/May/21

Oh wow ! Thanks a lot.

$$\mathrm{Oh}\:\mathrm{wow}\:!\:\mathrm{Thanks}\:\mathrm{a}\:\mathrm{lot}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com