
Question Number 18233 by Joel577 last updated on 17/Jul/17
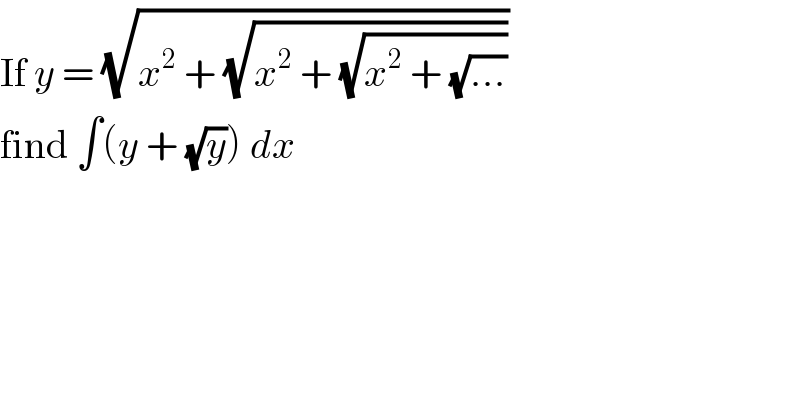
$$\mathrm{If}\:{y}\:=\:\sqrt{{x}^{\mathrm{2}} \:+\:\sqrt{{x}^{\mathrm{2}} \:+\:\sqrt{{x}^{\mathrm{2}} \:+\:\sqrt{...}}}} \\ $$$$\mathrm{find}\:\int\left({y}\:+\:\sqrt{{y}}\right)\:{dx} \\ $$
Commented by alex041103 last updated on 17/Jul/17
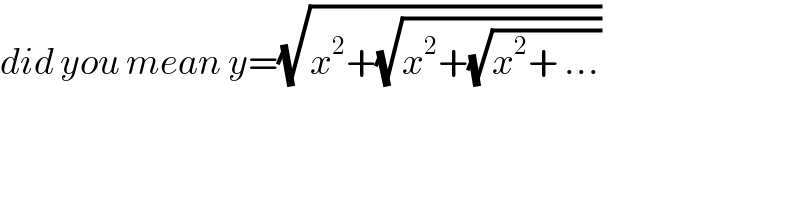
$${did}\:{you}\:{mean}\:{y}=\sqrt{{x}^{\mathrm{2}} +\sqrt{{x}^{\mathrm{2}} +\sqrt{{x}^{\mathrm{2}} +\:...}}} \\ $$
Commented by Joel577 last updated on 17/Jul/17
$${oh}\:{yes}.\:{thank}\:{you}.\:{I}\:{have}\:{corrected}\:{it} \\ $$
Answered by mrW1 last updated on 17/Jul/17
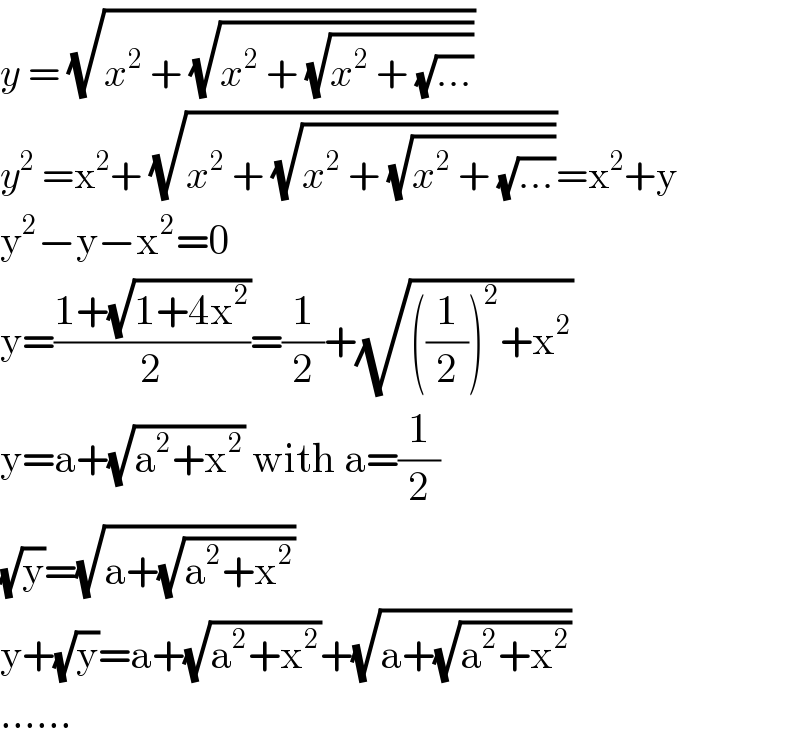
$${y}\:=\:\sqrt{{x}^{\mathrm{2}} \:+\:\sqrt{{x}^{\mathrm{2}} \:+\:\sqrt{{x}^{\mathrm{2}} \:+\:\sqrt{...}}}} \\ $$$${y}^{\mathrm{2}} \:=\mathrm{x}^{\mathrm{2}} +\:\sqrt{{x}^{\mathrm{2}} \:+\:\sqrt{{x}^{\mathrm{2}} \:+\:\sqrt{{x}^{\mathrm{2}} \:+\:\sqrt{...}}}}=\mathrm{x}^{\mathrm{2}} +\mathrm{y} \\ $$$$\mathrm{y}^{\mathrm{2}} −\mathrm{y}−\mathrm{x}^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{y}=\frac{\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{4x}^{\mathrm{2}} }}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}+\sqrt{\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} } \\ $$$$\mathrm{y}=\mathrm{a}+\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} }\:\mathrm{with}\:\mathrm{a}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\sqrt{\mathrm{y}}=\sqrt{\mathrm{a}+\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} }} \\ $$$$\mathrm{y}+\sqrt{\mathrm{y}}=\mathrm{a}+\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} }+\sqrt{\mathrm{a}+\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} }} \\ $$$$...... \\ $$
Commented by Joel577 last updated on 25/Jul/17
$${thank}\:{you}\:{very}\:{much} \\ $$
