Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 207442 by York12 last updated on 15/May/24

If y=f(x), (d^2 x/dy^2 )=e^(y+1) , and the tangent line to the curve of the function f(x) on the point (x_1 ,−1) is paralel to the straight line g(x)=x−3, then find f′(x).

$$\mathrm{If}\:{y}={f}\left({x}\right),\:\frac{{d}^{\mathrm{2}} {x}}{{dy}^{\mathrm{2}} }={e}^{{y}+\mathrm{1}} ,\:\mathrm{and}\:\mathrm{the}\:\mathrm{tangent}\:\mathrm{line}\:\mathrm{to}\:\mathrm{the}\:\mathrm{curve}\:\mathrm{of}\:\mathrm{the}\:\mathrm{function}\:{f}\left({x}\right)\:\mathrm{on}\:\mathrm{the}\:\mathrm{point} \\ $$$$\left({x}_{\mathrm{1}} ,−\mathrm{1}\right)\:\mathrm{is}\:\mathrm{paralel}\:\mathrm{to}\:\mathrm{the}\:\mathrm{straight}\:\mathrm{line}\:{g}\left({x}\right)={x}−\mathrm{3},\:\mathrm{then}\:\mathrm{find}\:{f}'\left({x}\right). \\ $$

Commented by York12 last updated on 15/May/24

The solution of that question was as follows but I do not understand particular things he said since (d^2 x/dy^2 )=e^(y+1) ⇒^(By integrating both sides ) ((d(x))/(d(y)))=e^(y+1) +c What I don′t understand here is to respect to what he integrated both sides ! I know when I have something like for example 3y^2 ×((d(y))/(d(x)))=2x+1 ⇔3y^2 ×d(y)=(2x+1)d(x) In this case we can integrate both sides ∫3y^2 d(y)=∫(2x+1)d(x)⇔y^3 =x^2 +x+c I do not understand how this process can be applied to the problem above after this step he did something seems wrong he said that since ((d(y))/(d(x)))=The slope of the tangent=1=((d(x))/(d(y))) he dealt with them as if they are variables divided by each other he used that in ((d(x))/(d(y)))=e^(y+1) +c((d(x))/(d(y)))=e^(y+1) +c ⇒1=e^0 +c⇒c=0 ∴((d(x))/(d(y)))=e^(y+1) , after that he did the same strange thinh ((d(y))/(d(x)))=(1/e^(y+1) ) ⇒(Which is strangely true) I would be thanfull for anyone who can explain that , thanks in advance

$$\mathrm{The}\:\mathrm{solution}\:\mathrm{of}\:\mathrm{that}\:\mathrm{question}\:\mathrm{was}\:\mathrm{as}\:\mathrm{follows}\:\mathrm{but}\:\mathrm{I}\:\mathrm{do}\:\mathrm{not}\:\mathrm{understand}\:\mathrm{particular}\:\mathrm{things} \\ $$$$\mathrm{he}\:\mathrm{said}\:\mathrm{since}\:\frac{{d}^{\mathrm{2}} {x}}{{dy}^{\mathrm{2}} }={e}^{{y}+\mathrm{1}} \:\overset{\mathrm{By}\:\mathrm{integrating}\:\mathrm{both}\:\mathrm{sides}\:} {\Rightarrow}\frac{{d}\left({x}\right)}{{d}\left({y}\right)}={e}^{{y}+\mathrm{1}} +{c} \\ $$$$\mathrm{What}\:\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{understand}\:\mathrm{here}\:\mathrm{is}\:\mathrm{to}\:\mathrm{respect}\:\mathrm{to}\:\mathrm{what} \\ $$$$\mathrm{he}\:\mathrm{integrated}\:\mathrm{both}\:\mathrm{sides}\:! \\ $$$$\mathrm{I}\:\mathrm{know}\:\mathrm{when}\:\mathrm{I}\:\mathrm{have}\:\mathrm{something}\:\mathrm{like}\:\mathrm{for}\:\mathrm{example} \\ $$$$\mathrm{3}{y}^{\mathrm{2}} ×\frac{{d}\left({y}\right)}{{d}\left({x}\right)}=\mathrm{2}{x}+\mathrm{1}\:\Leftrightarrow\mathrm{3}{y}^{\mathrm{2}} ×{d}\left({y}\right)=\left(\mathrm{2}{x}+\mathrm{1}\right){d}\left({x}\right) \\ $$$$\mathrm{In}\:\mathrm{this}\:\mathrm{case}\:\mathrm{we}\:\mathrm{can}\:\mathrm{integrate}\:\mathrm{both}\:\mathrm{sides} \\ $$$$\int\mathrm{3}{y}^{\mathrm{2}} \:{d}\left({y}\right)=\int\left(\mathrm{2}{x}+\mathrm{1}\right){d}\left({x}\right)\Leftrightarrow{y}^{\mathrm{3}} ={x}^{\mathrm{2}} +{x}+{c} \\ $$$$\mathrm{I}\:\mathrm{do}\:\mathrm{not}\:\mathrm{understand}\:\mathrm{how}\:\mathrm{this}\:\mathrm{process}\:\mathrm{can}\:\mathrm{be}\:\mathrm{applied}\:\mathrm{to}\:\mathrm{the}\:\mathrm{problem}\:\mathrm{above} \\ $$$$\mathrm{after}\:\mathrm{this}\:\mathrm{step}\:\mathrm{he}\:\mathrm{did}\:\mathrm{something}\:\mathrm{seems}\:\mathrm{wrong} \\ $$$$\mathrm{he}\:\mathrm{said}\:\mathrm{that}\:\mathrm{since}\:\frac{{d}\left({y}\right)}{{d}\left({x}\right)}=\mathrm{The}\:\mathrm{slope}\:\mathrm{of}\:\mathrm{the}\:\mathrm{tangent}=\mathrm{1}=\frac{{d}\left({x}\right)}{{d}\left({y}\right)} \\ $$$$\mathrm{he}\:\mathrm{dealt}\:\mathrm{with}\:\mathrm{them}\:\mathrm{as}\:\mathrm{if}\:\mathrm{they}\:\mathrm{are}\:\mathrm{variables}\:\mathrm{divided}\:\mathrm{by}\:\mathrm{each}\:\mathrm{other} \\ $$$$\mathrm{he}\:\mathrm{used}\:\mathrm{that}\:\mathrm{in}\:\frac{{d}\left({x}\right)}{{d}\left({y}\right)}={e}^{{y}+\mathrm{1}} +{c}\frac{{d}\left({x}\right)}{{d}\left({y}\right)}={e}^{{y}+\mathrm{1}} +{c}\:\Rightarrow\mathrm{1}=\mathrm{e}^{\mathrm{0}} +\mathrm{c}\Rightarrow\mathrm{c}=\mathrm{0} \\ $$$$\therefore\frac{{d}\left({x}\right)}{{d}\left({y}\right)}={e}^{{y}+\mathrm{1}} ,\:\mathrm{after}\:\mathrm{that}\:\mathrm{he}\:\mathrm{did}\:\mathrm{the}\:\mathrm{same}\:\mathrm{strange}\:\mathrm{thinh} \\ $$$$\frac{{d}\left({y}\right)}{{d}\left({x}\right)}=\frac{\mathrm{1}}{{e}^{{y}+\mathrm{1}} }\:\:\Rightarrow\left(\mathrm{Which}\:\mathrm{is}\:\mathrm{strangely}\:\mathrm{true}\right) \\ $$$$\mathrm{I}\:\mathrm{would}\:\mathrm{be}\:\mathrm{thanfull}\:\mathrm{for}\:\mathrm{anyone}\:\mathrm{who}\:\mathrm{can}\:\mathrm{explain}\:\mathrm{that}\:,\:\mathrm{thanks}\:\mathrm{in}\:\mathrm{advance} \\ $$$$ \\ $$

Commented by A5T last updated on 15/May/24

y=f(x), f(x_1 )=−1 ;f^′ (x_1 )=1 (d/dy)((dx/dy))=e^(y+1) . Assume x has been represented as a function of y⇒x=f(y); then you can differentiate taking x as a function of y. x=f(y)⇒(dx/dy)=f^′ (y)⇒(d/dy)((dx/dy))=f^(′′) y=e^(y+1) ∫∫f′′y=e^(y+1) +cy+k=f(y) ⇒x=f(y)=e^(y+1) +cy+k⇒(dx/dy)=e^(y+1) +c ⇒(dy/dx)=(1/(e^(y+1) +c)); (dy/dx)=1 when y=−1⇒(1/(1+c))=1⇒c=0 ⇒x=e^(y+1) +k⇒y=ln(x−k)−1; k=x_1 −1

$${y}={f}\left({x}\right),\:{f}\left({x}_{\mathrm{1}} \right)=−\mathrm{1}\:;{f}^{'} \left({x}_{\mathrm{1}} \right)=\mathrm{1} \\ $$$$\frac{{d}}{{dy}}\left(\frac{{dx}}{{dy}}\right)={e}^{{y}+\mathrm{1}} . \\ $$$${Assume}\:{x}\:{has}\:{been}\:{represented}\:{as}\:{a}\:{function}\: \\ $$$${of}\:{y}\Rightarrow{x}={f}\left({y}\right);\:{then}\:{you}\:{can}\:{differentiate} \\ $$$${taking}\:{x}\:{as}\:{a}\:{function}\:{of}\:{y}. \\ $$$${x}={f}\left({y}\right)\Rightarrow\frac{{dx}}{{dy}}={f}^{'} \left({y}\right)\Rightarrow\frac{{d}}{{dy}}\left(\frac{{dx}}{{dy}}\right)={f}^{''} {y}={e}^{{y}+\mathrm{1}} \\ $$$$\int\int{f}''{y}={e}^{{y}+\mathrm{1}} +{cy}+{k}={f}\left({y}\right) \\ $$$$\Rightarrow{x}={f}\left({y}\right)={e}^{{y}+\mathrm{1}} +{cy}+{k}\Rightarrow\frac{{dx}}{{dy}}={e}^{{y}+\mathrm{1}} +{c} \\ $$$$\Rightarrow\frac{{dy}}{{dx}}=\frac{\mathrm{1}}{{e}^{{y}+\mathrm{1}} +{c}}; \\ $$$$\frac{{dy}}{{dx}}=\mathrm{1}\:{when}\:{y}=−\mathrm{1}\Rightarrow\frac{\mathrm{1}}{\mathrm{1}+{c}}=\mathrm{1}\Rightarrow{c}=\mathrm{0} \\ $$$$\Rightarrow{x}={e}^{{y}+\mathrm{1}} +{k}\Rightarrow{y}={ln}\left({x}−{k}\right)−\mathrm{1};\:{k}={x}_{\mathrm{1}} −\mathrm{1} \\ $$$$ \\ $$

Commented by York12 last updated on 15/May/24

thank you sir

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$

Answered by mr W last updated on 15/May/24

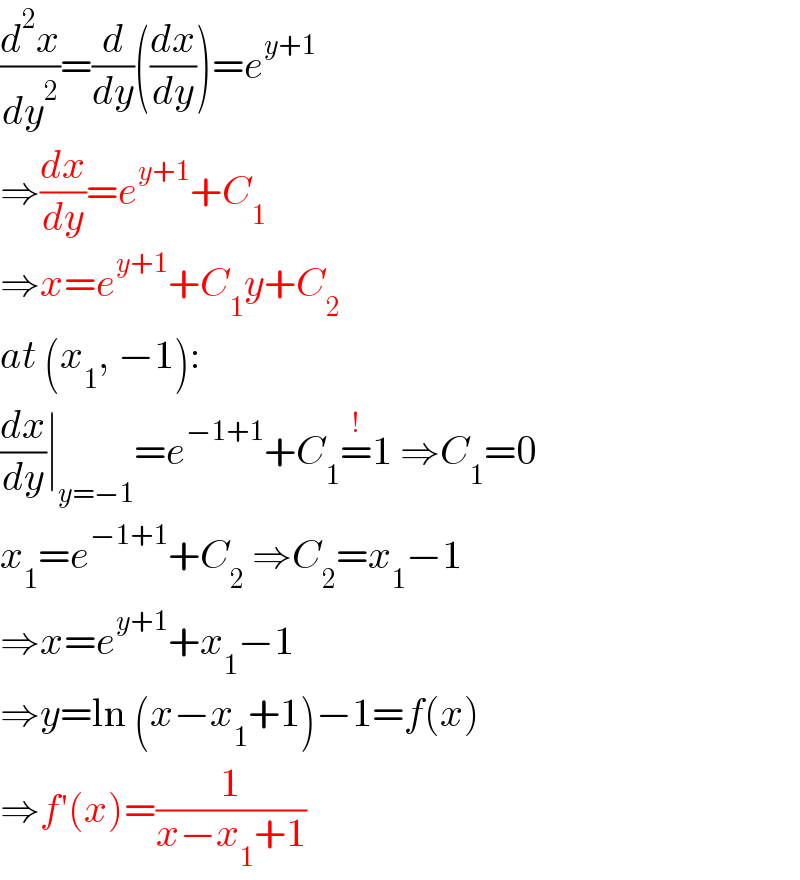
(d^2 x/dy^2 )=(d/dy)((dx/dy))=e^(y+1) ⇒(dx/dy)=e^(y+1) +C_1 ⇒x=e^(y+1) +C_1 y+C_2 at (x_1 , −1): (dx/dy)∣_(y=−1) =e^(−1+1) +C_1 =^! 1 ⇒C_1 =0 x_1 =e^(−1+1) +C_2 ⇒C_2 =x_1 −1 ⇒x=e^(y+1) +x_1 −1 ⇒y=ln (x−x_1 +1)−1=f(x) ⇒f′(x)=(1/(x−x_1 +1))

$$\frac{{d}^{\mathrm{2}} {x}}{{dy}^{\mathrm{2}} }=\frac{{d}}{{dy}}\left(\frac{{dx}}{{dy}}\right)={e}^{{y}+\mathrm{1}} \\ $$$$\Rightarrow\frac{{dx}}{{dy}}={e}^{{y}+\mathrm{1}} +{C}_{\mathrm{1}} \\ $$$$\Rightarrow{x}={e}^{{y}+\mathrm{1}} +{C}_{\mathrm{1}} {y}+{C}_{\mathrm{2}} \\ $$$${at}\:\left({x}_{\mathrm{1}} ,\:−\mathrm{1}\right): \\ $$$$\frac{{dx}}{{dy}}\mid_{{y}=−\mathrm{1}} ={e}^{−\mathrm{1}+\mathrm{1}} +{C}_{\mathrm{1}} \overset{!} {=}\mathrm{1}\:\Rightarrow{C}_{\mathrm{1}} =\mathrm{0} \\ $$$${x}_{\mathrm{1}} ={e}^{−\mathrm{1}+\mathrm{1}} +{C}_{\mathrm{2}} \:\Rightarrow{C}_{\mathrm{2}} ={x}_{\mathrm{1}} −\mathrm{1} \\ $$$$\Rightarrow{x}={e}^{{y}+\mathrm{1}} +{x}_{\mathrm{1}} −\mathrm{1} \\ $$$$\Rightarrow{y}=\mathrm{ln}\:\left({x}−{x}_{\mathrm{1}} +\mathrm{1}\right)−\mathrm{1}={f}\left({x}\right) \\ $$$$\Rightarrow{f}'\left({x}\right)=\frac{\mathrm{1}}{{x}−{x}_{\mathrm{1}} +\mathrm{1}} \\ $$

Commented by York12 last updated on 15/May/24

Really , Really appreciate it

$$\mathrm{Really}\:,\:\mathrm{Really}\:\mathrm{appreciate}\:\mathrm{it} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com