
Question Number 51436 by Tawa1 last updated on 26/Dec/18
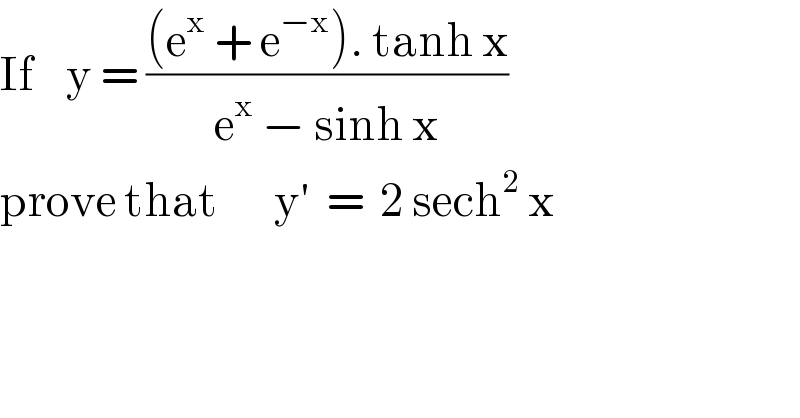
$$\mathrm{If}\:\:\:\:\mathrm{y}\:=\:\frac{\left(\mathrm{e}^{\mathrm{x}} \:+\:\mathrm{e}^{−\mathrm{x}} \right).\:\mathrm{tanh}\:\mathrm{x}}{\mathrm{e}^{\mathrm{x}} \:−\:\mathrm{sinh}\:\mathrm{x}} \\ $$$$\mathrm{prove}\:\mathrm{that}\:\:\:\:\:\:\:\mathrm{y}'\:\:=\:\:\mathrm{2}\:\mathrm{sech}^{\mathrm{2}} \:\mathrm{x} \\ $$
Answered by peter frank last updated on 26/Dec/18
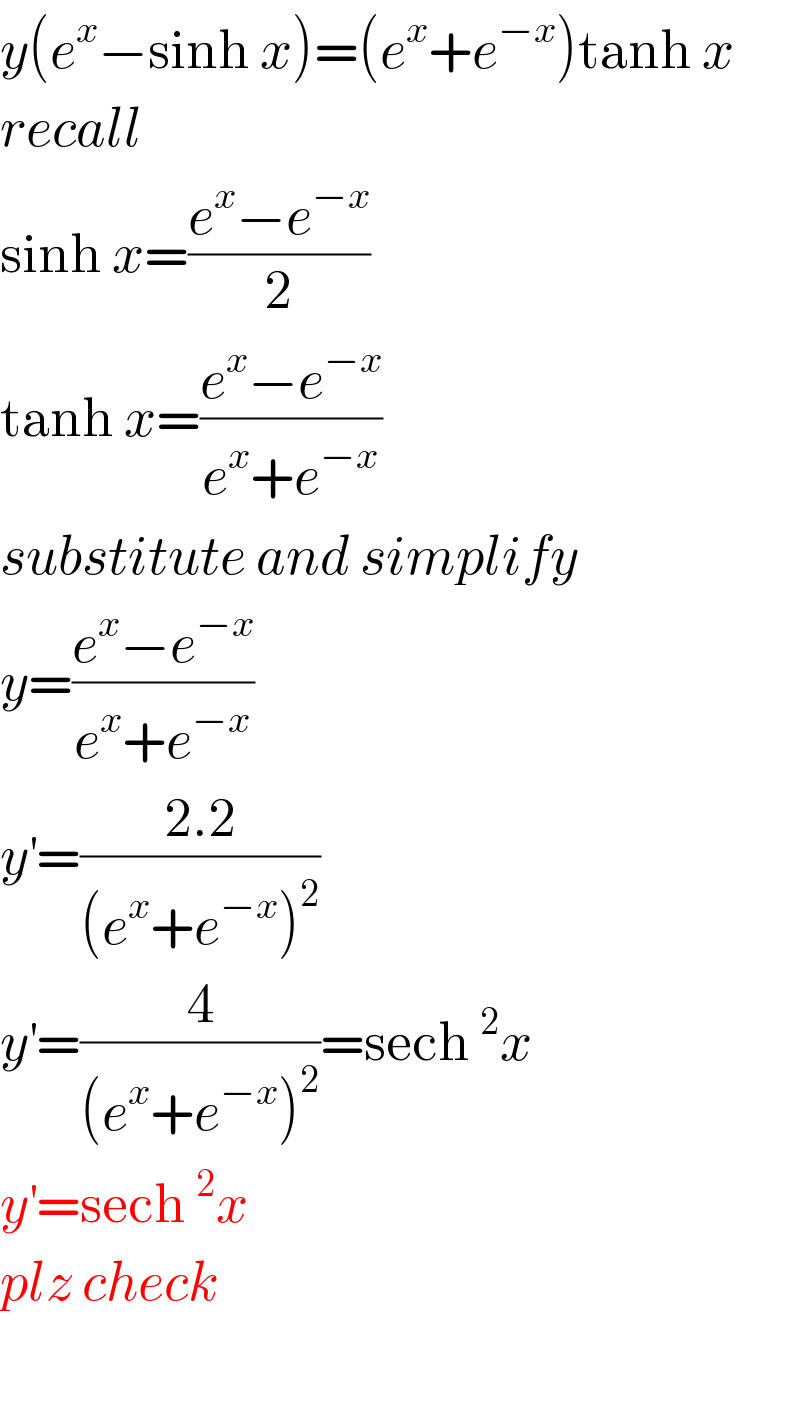
$${y}\left({e}^{{x}} −\mathrm{sinh}\:{x}\right)=\left({e}^{{x}} +{e}^{−{x}} \right)\mathrm{tanh}\:{x} \\ $$$${recall} \\ $$$$\mathrm{sinh}\:{x}=\frac{{e}^{{x}} −{e}^{−{x}} }{\mathrm{2}} \\ $$$$\mathrm{tanh}\:{x}=\frac{{e}^{{x}} −{e}^{−{x}} }{{e}^{{x}} +{e}^{−{x}} } \\ $$$${substitute}\:{and}\:{simplify} \\ $$$${y}=\frac{{e}^{{x}} −{e}^{−{x}} }{{e}^{{x}} +{e}^{−{x}} } \\ $$$${y}^{'} =\frac{\mathrm{2}.\mathrm{2}}{\left({e}^{{x}} +{e}^{−{x}} \right)^{\mathrm{2}} }\: \\ $$$${y}^{'} =\frac{\mathrm{4}}{\left({e}^{{x}} +{e}^{−{x}} \right)^{\mathrm{2}} }=\mathrm{sech}\:^{\mathrm{2}} {x} \\ $$$${y}^{'} =\mathrm{sech}\:^{\mathrm{2}} {x} \\ $$$${plz}\:{check} \\ $$$$ \\ $$
Commented by Tawa1 last updated on 27/Dec/18

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
