
Question Number 196683 by MATHEMATICSAM last updated on 29/Aug/23
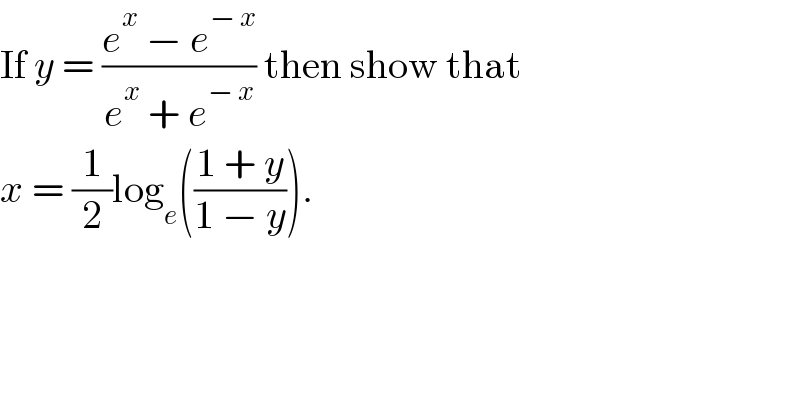
$$\mathrm{If}\:{y}\:=\:\frac{{e}^{{x}} \:−\:{e}^{−\:{x}} }{{e}^{{x}} \:+\:{e}^{−\:{x}} }\:\mathrm{then}\:\mathrm{show}\:\mathrm{that} \\ $$$${x}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{log}_{{e}} \left(\frac{\mathrm{1}\:+\:{y}}{\mathrm{1}\:−\:{y}}\right). \\ $$
Answered by Frix last updated on 29/Aug/23

$${y}=\frac{\mathrm{e}^{\mathrm{2}{x}} −\mathrm{1}}{\mathrm{e}^{\mathrm{2}{x}} +\mathrm{1}} \\ $$$$\mathrm{e}^{\mathrm{2}{x}} =\frac{\mathrm{1}+{y}}{\mathrm{1}−{y}} \\ $$$$\mathrm{2}{x}=\mathrm{ln}\:\frac{\mathrm{1}+{y}}{\mathrm{1}−{y}} \\ $$$${x}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\frac{\mathrm{1}+{y}}{\mathrm{1}−{y}} \\ $$
Answered by som(math1967) last updated on 29/Aug/23
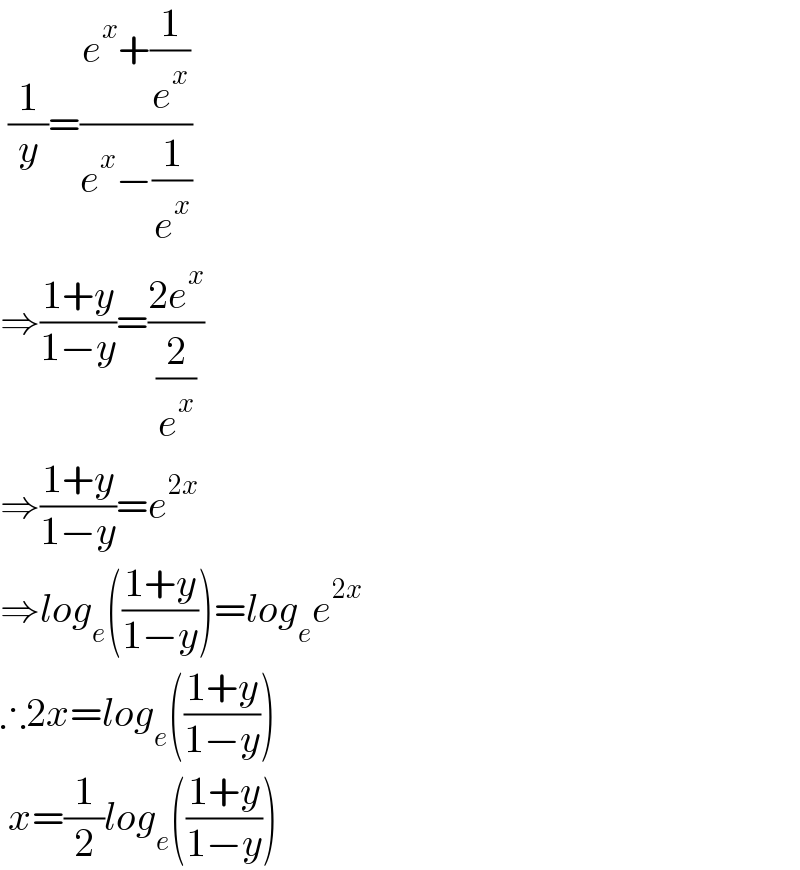
$$\:\frac{\mathrm{1}}{{y}}=\frac{{e}^{{x}} +\frac{\mathrm{1}}{{e}^{{x}} }}{{e}^{{x}} −\frac{\mathrm{1}}{{e}^{{x}} }} \\ $$$$\Rightarrow\frac{\mathrm{1}+{y}}{\mathrm{1}−{y}}=\frac{\mathrm{2}{e}^{{x}} }{\frac{\mathrm{2}}{{e}^{{x}} }} \\ $$$$\Rightarrow\frac{\mathrm{1}+{y}}{\mathrm{1}−{y}}={e}^{\mathrm{2}{x}} \\ $$$$\Rightarrow{log}_{{e}} \left(\frac{\mathrm{1}+{y}}{\mathrm{1}−{y}}\right)={log}_{{e}} {e}^{\mathrm{2}{x}} \\ $$$$\therefore\mathrm{2}{x}={log}_{{e}} \left(\frac{\mathrm{1}+{y}}{\mathrm{1}−{y}}\right) \\ $$$$\:{x}=\frac{\mathrm{1}}{\mathrm{2}}{log}_{{e}} \left(\frac{\mathrm{1}+{y}}{\mathrm{1}−{y}}\right) \\ $$
