
Question Number 144525 by imjagoll last updated on 26/Jun/21
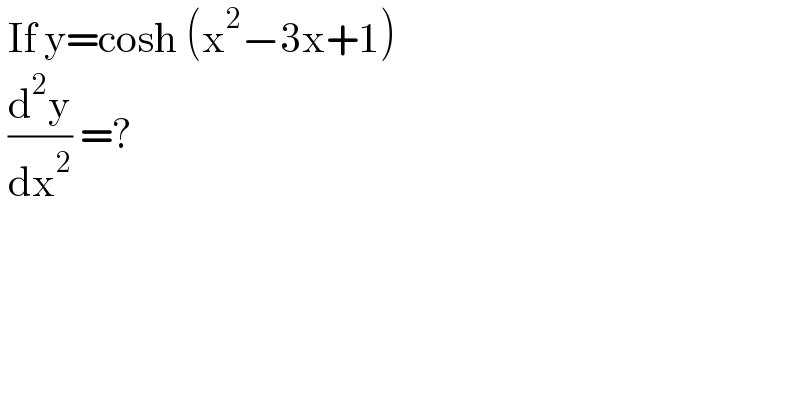
$$\:\mathrm{If}\:\mathrm{y}=\mathrm{cosh}\:\left(\mathrm{x}^{\mathrm{2}} −\mathrm{3x}+\mathrm{1}\right) \\ $$$$\:\frac{\mathrm{d}^{\mathrm{2}} \mathrm{y}}{\mathrm{dx}^{\mathrm{2}} }\:=? \\ $$
Answered by EDWIN88 last updated on 26/Jun/21
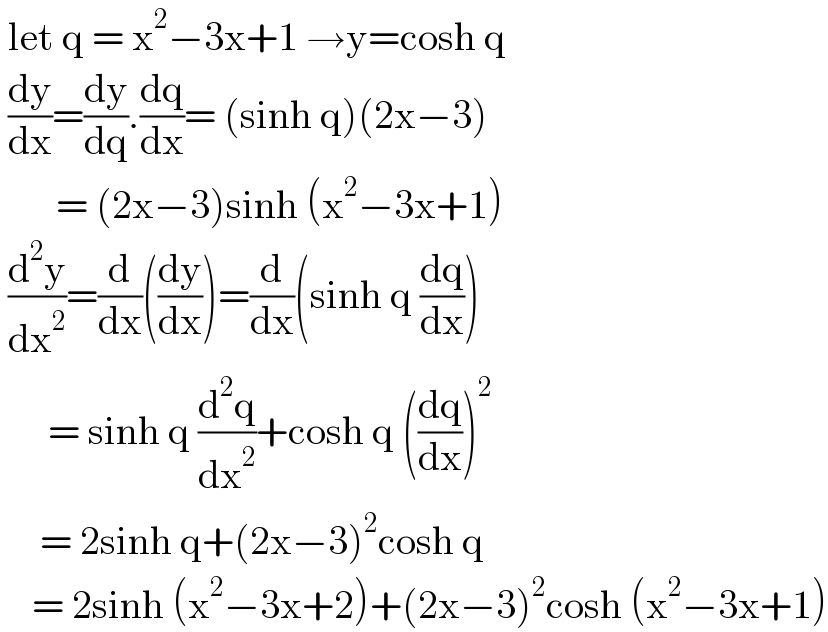
$$\:\mathrm{let}\:\mathrm{q}\:=\:\mathrm{x}^{\mathrm{2}} −\mathrm{3x}+\mathrm{1}\:\rightarrow\mathrm{y}=\mathrm{cosh}\:\mathrm{q} \\ $$$$\:\frac{\mathrm{dy}}{\mathrm{dx}}=\frac{\mathrm{dy}}{\mathrm{dq}}.\frac{\mathrm{dq}}{\mathrm{dx}}=\:\left(\mathrm{sinh}\:\mathrm{q}\right)\left(\mathrm{2x}−\mathrm{3}\right) \\ $$$$\:\:\:\:\:\:\:=\:\left(\mathrm{2x}−\mathrm{3}\right)\mathrm{sinh}\:\left(\mathrm{x}^{\mathrm{2}} −\mathrm{3x}+\mathrm{1}\right) \\ $$$$\:\frac{\mathrm{d}^{\mathrm{2}} \mathrm{y}}{\mathrm{dx}^{\mathrm{2}} }=\frac{\mathrm{d}}{\mathrm{dx}}\left(\frac{\mathrm{dy}}{\mathrm{dx}}\right)=\frac{\mathrm{d}}{\mathrm{dx}}\left(\mathrm{sinh}\:\mathrm{q}\:\frac{\mathrm{dq}}{\mathrm{dx}}\right) \\ $$$$\:\:\:\:\:\:=\:\mathrm{sinh}\:\mathrm{q}\:\frac{\mathrm{d}^{\mathrm{2}} \mathrm{q}}{\mathrm{dx}^{\mathrm{2}} }+\mathrm{cosh}\:\mathrm{q}\:\left(\frac{\mathrm{dq}}{\mathrm{dx}}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:=\:\mathrm{2sinh}\:\mathrm{q}+\left(\mathrm{2x}−\mathrm{3}\right)^{\mathrm{2}} \mathrm{cosh}\:\mathrm{q} \\ $$$$\:\:\:\:=\:\mathrm{2sinh}\:\left(\mathrm{x}^{\mathrm{2}} −\mathrm{3x}+\mathrm{2}\right)+\left(\mathrm{2x}−\mathrm{3}\right)^{\mathrm{2}} \mathrm{cosh}\:\left(\mathrm{x}^{\mathrm{2}} −\mathrm{3x}+\mathrm{1}\right) \\ $$
Answered by mathmax by abdo last updated on 26/Jun/21
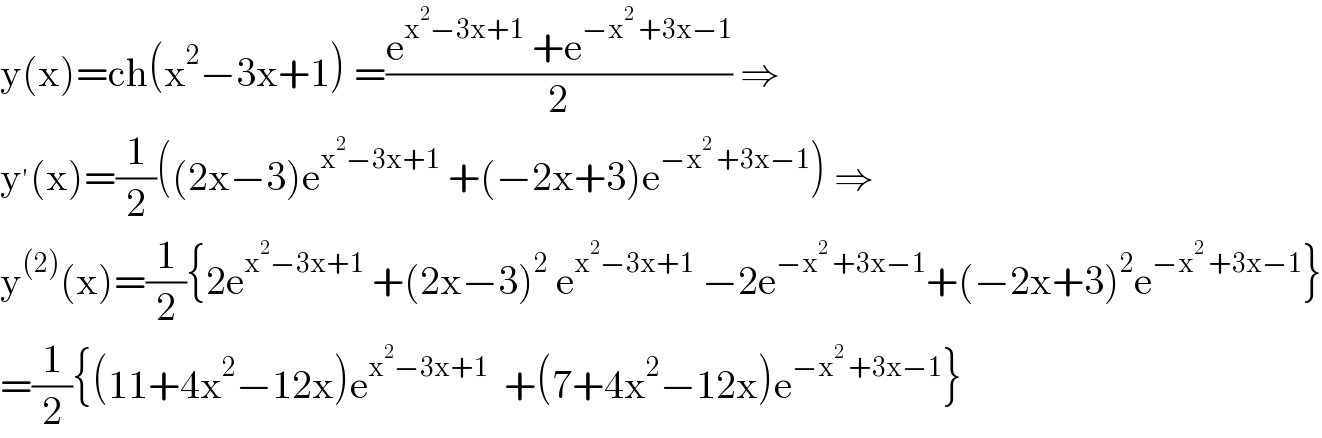
$$\mathrm{y}\left(\mathrm{x}\right)=\mathrm{ch}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{3x}+\mathrm{1}\right)\:=\frac{\mathrm{e}^{\mathrm{x}^{\mathrm{2}} −\mathrm{3x}+\mathrm{1}} \:+\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} \:+\mathrm{3x}−\mathrm{1}} }{\mathrm{2}}\:\Rightarrow \\ $$$$\mathrm{y}^{'} \left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\left(\mathrm{2x}−\mathrm{3}\right)\mathrm{e}^{\mathrm{x}^{\mathrm{2}} −\mathrm{3x}+\mathrm{1}} \:+\left(−\mathrm{2x}+\mathrm{3}\right)\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} \:+\mathrm{3x}−\mathrm{1}} \right)\:\Rightarrow \\ $$$$\mathrm{y}^{\left(\mathrm{2}\right)} \left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left\{\mathrm{2e}^{\mathrm{x}^{\mathrm{2}} −\mathrm{3x}+\mathrm{1}} \:+\left(\mathrm{2x}−\mathrm{3}\right)^{\mathrm{2}} \:\mathrm{e}^{\mathrm{x}^{\mathrm{2}} −\mathrm{3x}+\mathrm{1}} \:−\mathrm{2e}^{−\mathrm{x}^{\mathrm{2}} \:+\mathrm{3x}−\mathrm{1}} +\left(−\mathrm{2x}+\mathrm{3}\right)^{\mathrm{2}} \mathrm{e}^{−\mathrm{x}^{\mathrm{2}} \:+\mathrm{3x}−\mathrm{1}} \right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left\{\left(\mathrm{11}+\mathrm{4x}^{\mathrm{2}} −\mathrm{12x}\right)\mathrm{e}^{\mathrm{x}^{\mathrm{2}} −\mathrm{3x}+\mathrm{1}} \:\:+\left(\mathrm{7}+\mathrm{4x}^{\mathrm{2}} −\mathrm{12x}\right)\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} \:+\mathrm{3x}−\mathrm{1}} \right\} \\ $$
