
Question Number 188889 by mnjuly1970 last updated on 08/Mar/23
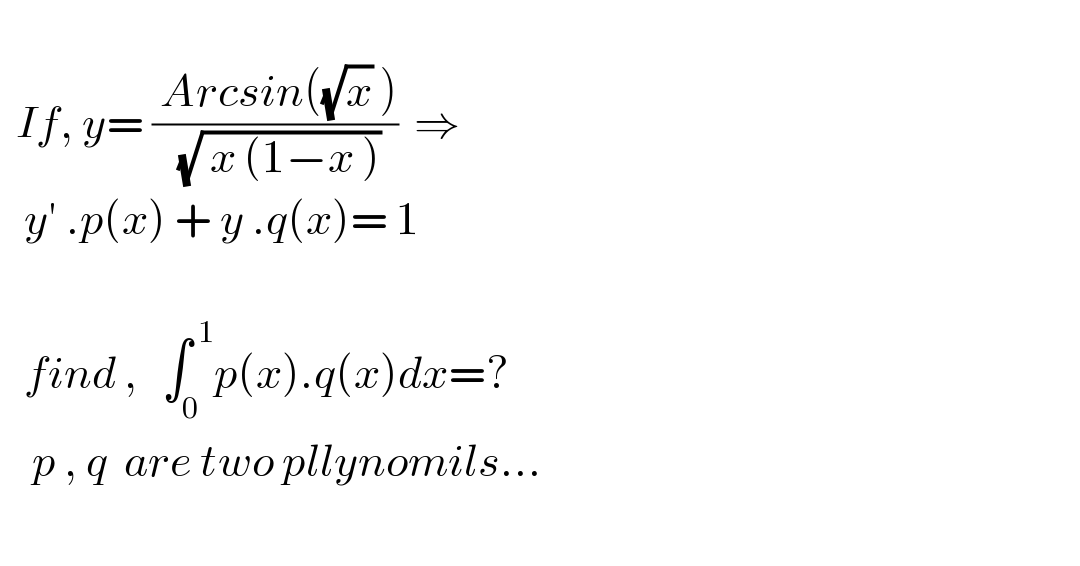
$$ \\ $$$$\:\:{If},\:{y}=\:\frac{\:{Arcsin}\left(\sqrt{{x}}\:\right)}{\:\sqrt{\:{x}\:\left(\mathrm{1}−{x}\:\right)}}\:\:\Rightarrow \\ $$$$\:\:\:{y}'\:.{p}\left({x}\right)\:+\:{y}\:.{q}\left({x}\right)=\:\mathrm{1} \\ $$$$ \\ $$$$\:\:\:{find}\:,\:\:\:\int_{\mathrm{0}} ^{\:\mathrm{1}} {p}\left({x}\right).{q}\left({x}\right){dx}=? \\ $$$$\:\:\:\:{p}\:,\:{q}\:\:{are}\:{two}\:{pllynomils}... \\ $$$$ \\ $$
Answered by qaz last updated on 08/Mar/23
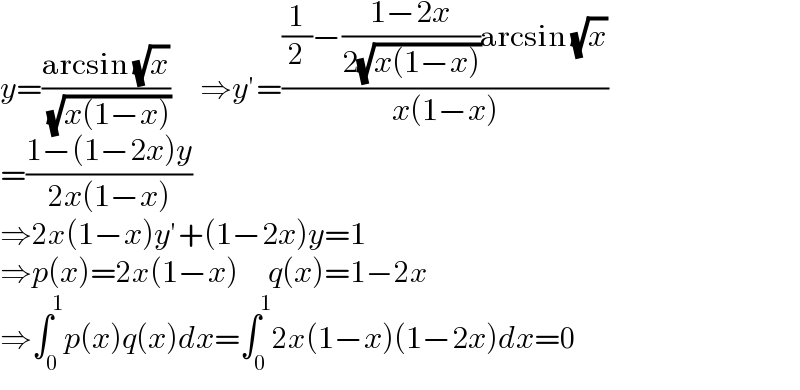
$${y}=\frac{\mathrm{arcsin}\:\sqrt{{x}}}{\:\sqrt{{x}\left(\mathrm{1}−{x}\right)}}\:\:\:\:\:\Rightarrow{y}'=\frac{\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}−\mathrm{2}{x}}{\mathrm{2}\sqrt{{x}\left(\mathrm{1}−{x}\right)}}\mathrm{arcsin}\:\sqrt{{x}}}{{x}\left(\mathrm{1}−{x}\right)} \\ $$$$=\frac{\mathrm{1}−\left(\mathrm{1}−\mathrm{2}{x}\right){y}}{\mathrm{2}{x}\left(\mathrm{1}−{x}\right)} \\ $$$$\Rightarrow\mathrm{2}{x}\left(\mathrm{1}−{x}\right){y}'+\left(\mathrm{1}−\mathrm{2}{x}\right){y}=\mathrm{1} \\ $$$$\Rightarrow{p}\left({x}\right)=\mathrm{2}{x}\left(\mathrm{1}−{x}\right)\:\:\:\:\:{q}\left({x}\right)=\mathrm{1}−\mathrm{2}{x} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} {p}\left({x}\right){q}\left({x}\right){dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{2}{x}\left(\mathrm{1}−{x}\right)\left(\mathrm{1}−\mathrm{2}{x}\right){dx}=\mathrm{0} \\ $$
Commented by mnjuly1970 last updated on 08/Mar/23

$$\:{mercey}\:{sir} \\ $$
