
Question Number 32110 by pieroo last updated on 19/Mar/18

$$\mathrm{If}\:\mathrm{y}=\mathrm{1}+\mathrm{x}^{\mathrm{2}} +\mathrm{x}^{\mathrm{3}} \:\mathrm{and}\:\mathrm{x}=\mathrm{1}+\alpha,\:\mathrm{where}\:\alpha\:\mathrm{is}\:\mathrm{small},\:\mathrm{show} \\ $$$$\mathrm{that}\:\mathrm{y}\approx\mathrm{3}+\mathrm{5}\alpha.\:\mathrm{Hence},\:\mathrm{find}\:\mathrm{the}\:\mathrm{increase}\:\mathrm{in}\:\mathrm{y}\:\mathrm{when} \\ $$$$\mathrm{x}\:\mathrm{is}\:\mathrm{increased}\:\mathrm{from}\:\mathrm{1}\:\mathrm{to}\:\mathrm{1}.\mathrm{02} \\ $$
Answered by mrW2 last updated on 19/Mar/18
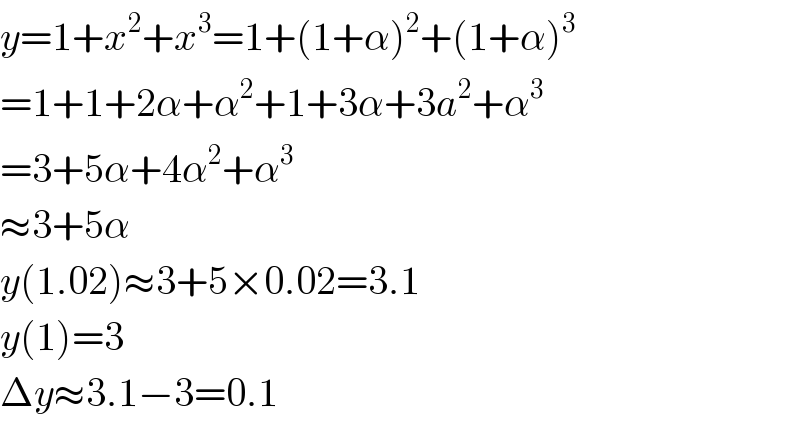
$${y}=\mathrm{1}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} =\mathrm{1}+\left(\mathrm{1}+\alpha\right)^{\mathrm{2}} +\left(\mathrm{1}+\alpha\right)^{\mathrm{3}} \\ $$$$=\mathrm{1}+\mathrm{1}+\mathrm{2}\alpha+\alpha^{\mathrm{2}} +\mathrm{1}+\mathrm{3}\alpha+\mathrm{3}{a}^{\mathrm{2}} +\alpha^{\mathrm{3}} \\ $$$$=\mathrm{3}+\mathrm{5}\alpha+\mathrm{4}\alpha^{\mathrm{2}} +\alpha^{\mathrm{3}} \\ $$$$\approx\mathrm{3}+\mathrm{5}\alpha \\ $$$${y}\left(\mathrm{1}.\mathrm{02}\right)\approx\mathrm{3}+\mathrm{5}×\mathrm{0}.\mathrm{02}=\mathrm{3}.\mathrm{1} \\ $$$${y}\left(\mathrm{1}\right)=\mathrm{3} \\ $$$$\Delta{y}\approx\mathrm{3}.\mathrm{1}−\mathrm{3}=\mathrm{0}.\mathrm{1} \\ $$
Commented by pieroo last updated on 19/Mar/18

$$\mathrm{thanks}\:\mathrm{Sir} \\ $$
