
Question Number 207109 by MATHEMATICSAM last updated on 06/May/24
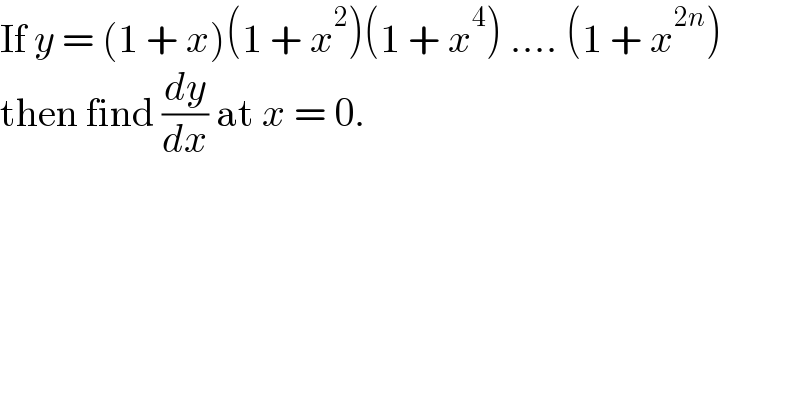
$$\mathrm{If}\:{y}\:=\:\left(\mathrm{1}\:+\:{x}\right)\left(\mathrm{1}\:+\:{x}^{\mathrm{2}} \right)\left(\mathrm{1}\:+\:{x}^{\mathrm{4}} \right)\:....\:\left(\mathrm{1}\:+\:{x}^{\mathrm{2}{n}} \right) \\ $$$$\mathrm{then}\:\mathrm{find}\:\frac{{dy}}{{dx}}\:\mathrm{at}\:{x}\:=\:\mathrm{0}. \\ $$
Answered by Berbere last updated on 06/May/24
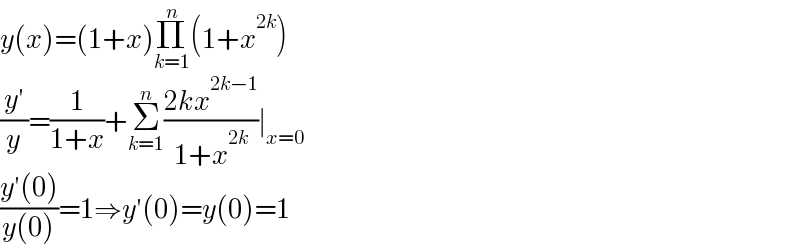
$${y}\left({x}\right)=\left(\mathrm{1}+{x}\right)\underset{{k}=\mathrm{1}} {\overset{{n}} {\prod}}\left(\mathrm{1}+{x}^{\mathrm{2}{k}} \right) \\ $$$$\frac{{y}'}{{y}}=\frac{\mathrm{1}}{\mathrm{1}+{x}}+\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{2}{kx}^{\mathrm{2}{k}−\mathrm{1}} }{\mathrm{1}+{x}^{\mathrm{2}{k}} }\mid_{{x}=\mathrm{0}} \\ $$$$\frac{{y}'\left(\mathrm{0}\right)}{{y}\left(\mathrm{0}\right)}=\mathrm{1}\Rightarrow{y}'\left(\mathrm{0}\right)={y}\left(\mathrm{0}\right)=\mathrm{1} \\ $$
Answered by mr W last updated on 06/May/24
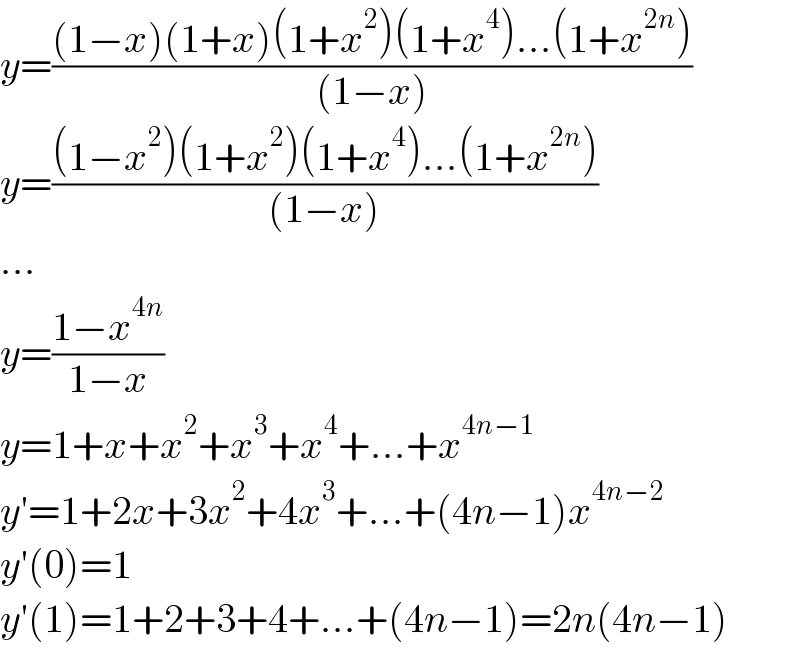
$${y}=\frac{\left(\mathrm{1}−{x}\right)\left(\mathrm{1}+{x}\right)\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\left(\mathrm{1}+{x}^{\mathrm{4}} \right)...\left(\mathrm{1}+{x}^{\mathrm{2}{n}} \right)}{\left(\mathrm{1}−{x}\right)} \\ $$$${y}=\frac{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\left(\mathrm{1}+{x}^{\mathrm{4}} \right)...\left(\mathrm{1}+{x}^{\mathrm{2}{n}} \right)}{\left(\mathrm{1}−{x}\right)} \\ $$$$... \\ $$$${y}=\frac{\mathrm{1}−{x}^{\mathrm{4}{n}} }{\mathrm{1}−{x}} \\ $$$${y}=\mathrm{1}+{x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +{x}^{\mathrm{4}} +...+{x}^{\mathrm{4}{n}−\mathrm{1}} \\ $$$${y}'=\mathrm{1}+\mathrm{2}{x}+\mathrm{3}{x}^{\mathrm{2}} +\mathrm{4}{x}^{\mathrm{3}} +...+\left(\mathrm{4}{n}−\mathrm{1}\right){x}^{\mathrm{4}{n}−\mathrm{2}} \\ $$$${y}'\left(\mathrm{0}\right)=\mathrm{1} \\ $$$${y}'\left(\mathrm{1}\right)=\mathrm{1}+\mathrm{2}+\mathrm{3}+\mathrm{4}+...+\left(\mathrm{4}{n}−\mathrm{1}\right)=\mathrm{2}{n}\left(\mathrm{4}{n}−\mathrm{1}\right) \\ $$
Commented by manxsol last updated on 19/May/24

$$ \\ $$$$\:\underline{\downdownarrows} \\ $$
Commented by mr W last updated on 19/May/24

$${thanks}! \\ $$
Answered by mathzup last updated on 08/May/24
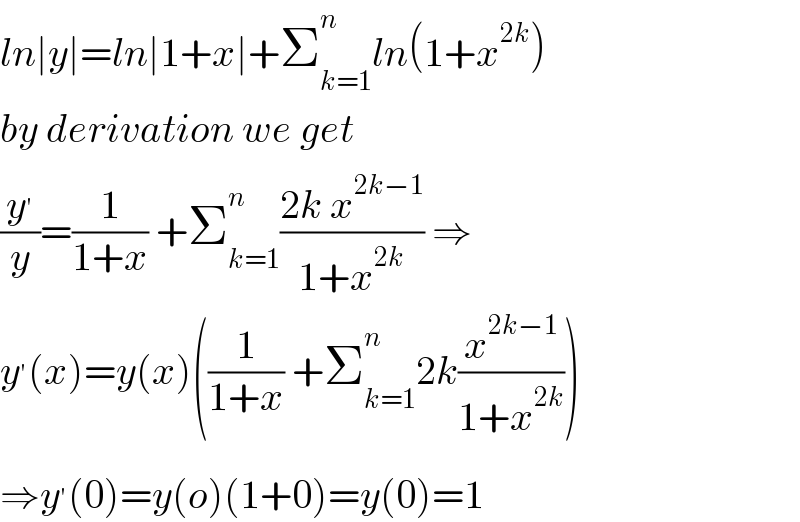
$${ln}\mid{y}\mid={ln}\mid\mathrm{1}+{x}\mid+\sum_{{k}=\mathrm{1}} ^{{n}} {ln}\left(\mathrm{1}+{x}^{\mathrm{2}{k}} \right)\: \\ $$$${by}\:{derivation}\:{we}\:{get} \\ $$$$\frac{{y}^{'} }{{y}}=\frac{\mathrm{1}}{\mathrm{1}+{x}}\:+\sum_{{k}=\mathrm{1}} ^{{n}} \frac{\mathrm{2}{k}\:{x}^{\mathrm{2}{k}−\mathrm{1}} }{\mathrm{1}+{x}^{\mathrm{2}{k}} }\:\Rightarrow \\ $$$${y}^{'} \left({x}\right)={y}\left({x}\right)\left(\frac{\mathrm{1}}{\mathrm{1}+{x}}\:+\sum_{{k}=\mathrm{1}} ^{{n}} \mathrm{2}{k}\frac{{x}^{\mathrm{2}{k}−\mathrm{1}} }{\mathrm{1}+{x}^{\mathrm{2}{k}} }\right) \\ $$$$\Rightarrow{y}^{'} \left(\mathrm{0}\right)={y}\left({o}\right)\left(\mathrm{1}+\mathrm{0}\right)={y}\left(\mathrm{0}\right)=\mathrm{1} \\ $$
