
Question Number 109585 by nimnim last updated on 24/Aug/20
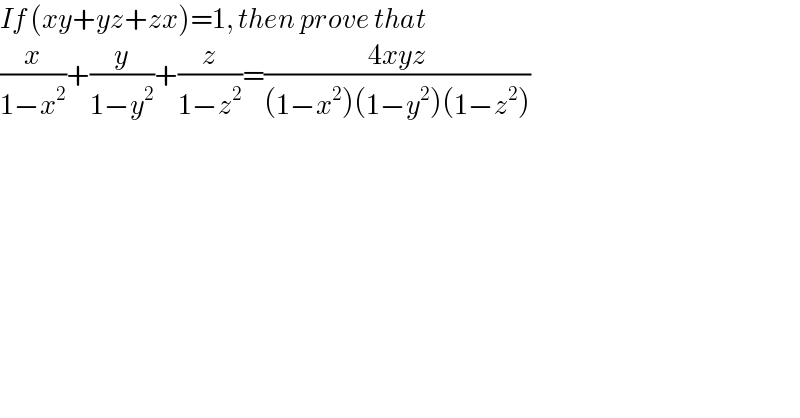
$${If}\:\left({xy}+{yz}+{zx}\right)=\mathrm{1},\:{then}\:{prove}\:{that} \\ $$$$\frac{{x}}{\mathrm{1}−{x}^{\mathrm{2}} }+\frac{{y}}{\mathrm{1}−{y}^{\mathrm{2}} }+\frac{{z}}{\mathrm{1}−{z}^{\mathrm{2}} }=\frac{\mathrm{4}{xyz}}{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\left(\mathrm{1}−{y}^{\mathrm{2}} \right)\left(\mathrm{1}−{z}^{\mathrm{2}} \right)} \\ $$
Answered by som(math1967) last updated on 25/Aug/20
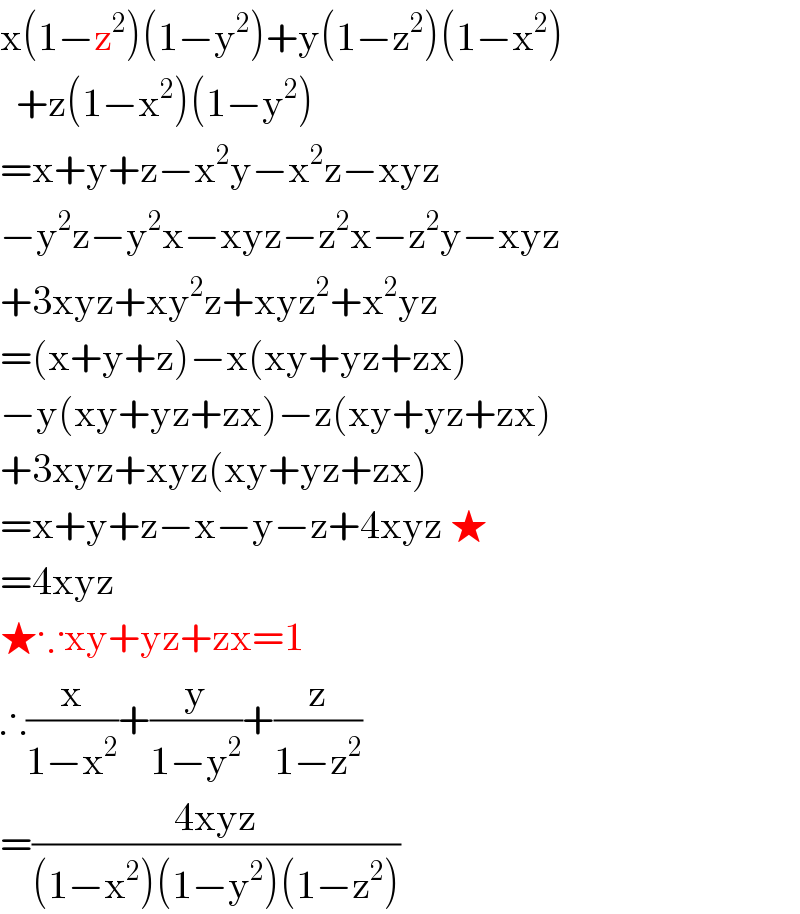
$$\mathrm{x}\left(\mathrm{1}−\mathrm{z}^{\mathrm{2}} \right)\left(\mathrm{1}−\mathrm{y}^{\mathrm{2}} \right)+\mathrm{y}\left(\mathrm{1}−\mathrm{z}^{\mathrm{2}} \right)\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right) \\ $$$$\:\:+\mathrm{z}\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)\left(\mathrm{1}−\mathrm{y}^{\mathrm{2}} \right) \\ $$$$=\mathrm{x}+\mathrm{y}+\mathrm{z}−\mathrm{x}^{\mathrm{2}} \mathrm{y}−\mathrm{x}^{\mathrm{2}} \mathrm{z}−\mathrm{xyz} \\ $$$$−\mathrm{y}^{\mathrm{2}} \mathrm{z}−\mathrm{y}^{\mathrm{2}} \mathrm{x}−\mathrm{xyz}−\mathrm{z}^{\mathrm{2}} \mathrm{x}−\mathrm{z}^{\mathrm{2}} \mathrm{y}−\mathrm{xyz} \\ $$$$+\mathrm{3xyz}+\mathrm{xy}^{\mathrm{2}} \mathrm{z}+\mathrm{xyz}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} \mathrm{yz} \\ $$$$=\left(\mathrm{x}+\mathrm{y}+\mathrm{z}\right)−\mathrm{x}\left(\mathrm{xy}+\mathrm{yz}+\mathrm{zx}\right) \\ $$$$−\mathrm{y}\left(\mathrm{xy}+\mathrm{yz}+\mathrm{zx}\right)−\mathrm{z}\left(\mathrm{xy}+\mathrm{yz}+\mathrm{zx}\right) \\ $$$$+\mathrm{3xyz}+\mathrm{xyz}\left(\mathrm{xy}+\mathrm{yz}+\mathrm{zx}\right) \\ $$$$=\mathrm{x}+\mathrm{y}+\mathrm{z}−\mathrm{x}−\mathrm{y}−\mathrm{z}+\mathrm{4xyz}\:\bigstar \\ $$$$=\mathrm{4xyz} \\ $$$$\bigstar\because\mathrm{xy}+\mathrm{yz}+\mathrm{zx}=\mathrm{1} \\ $$$$\therefore\frac{\mathrm{x}}{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }+\frac{\mathrm{y}}{\mathrm{1}−\mathrm{y}^{\mathrm{2}} }+\frac{\mathrm{z}}{\mathrm{1}−\mathrm{z}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{4xyz}}{\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)\left(\mathrm{1}−\mathrm{y}^{\mathrm{2}} \right)\left(\mathrm{1}−\mathrm{z}^{\mathrm{2}} \right)} \\ $$
Commented by nimnim last updated on 24/Aug/20

$${Thanks}. \\ $$
Commented by nimnim last updated on 24/Aug/20

$${Sir},\:{I}\:{think}\:{the}\:{first}\:{line} \\ $$$${x}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\left(\mathrm{1}−{y}^{\mathrm{2}} \right)+..\:{is}\:{typo}\:{mistake}. \\ $$$${Thank}\:{you}\:{once}\:{again}. \\ $$
Commented by som(math1967) last updated on 25/Aug/20

$$\mathrm{yes}\: \\ $$
