
Question Number 112802 by Aina Samuel Temidayo last updated on 09/Sep/20
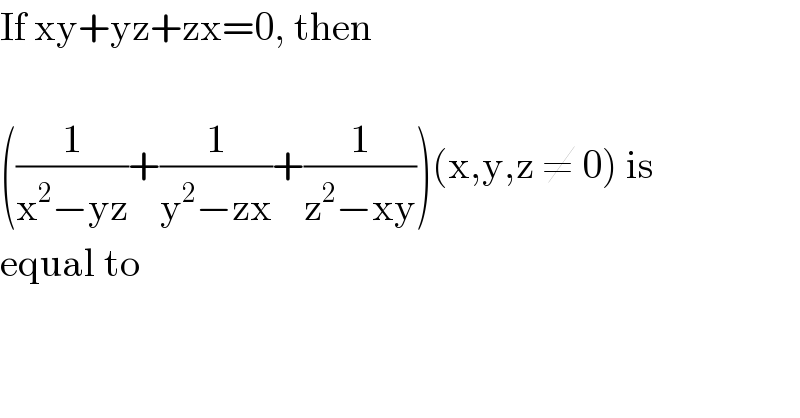
$$\mathrm{If}\:\mathrm{xy}+\mathrm{yz}+\mathrm{zx}=\mathrm{0},\:\mathrm{then} \\ $$$$ \\ $$$$\left(\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} −\mathrm{yz}}+\frac{\mathrm{1}}{\mathrm{y}^{\mathrm{2}} −\mathrm{zx}}+\frac{\mathrm{1}}{\mathrm{z}^{\mathrm{2}} −\mathrm{xy}}\right)\left(\mathrm{x},\mathrm{y},\mathrm{z}\:\neq\:\mathrm{0}\right)\:\mathrm{is} \\ $$$$\mathrm{equal}\:\mathrm{to} \\ $$$$ \\ $$
Answered by MJS_new last updated on 09/Sep/20
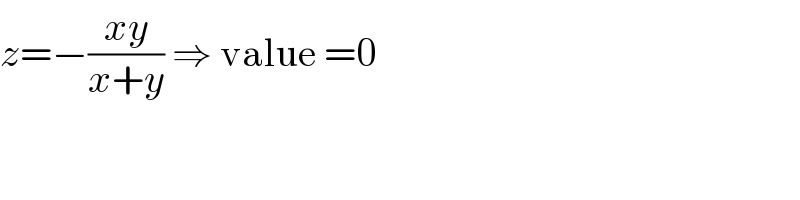
$${z}=−\frac{{xy}}{{x}+{y}}\:\Rightarrow\:\mathrm{value}\:=\mathrm{0} \\ $$
Answered by Dwaipayan Shikari last updated on 09/Sep/20
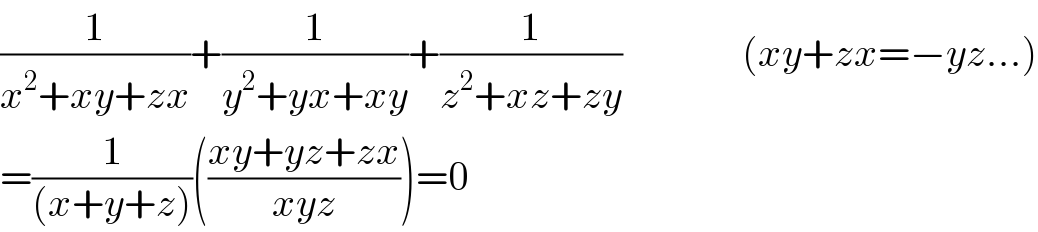
$$\frac{\mathrm{1}}{{x}^{\mathrm{2}} +{xy}+{zx}}+\frac{\mathrm{1}}{{y}^{\mathrm{2}} +{yx}+{xy}}+\frac{\mathrm{1}}{{z}^{\mathrm{2}} +{xz}+{zy}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left({xy}+{zx}=−{yz}...\right) \\ $$$$=\frac{\mathrm{1}}{\left({x}+{y}+{z}\right)}\left(\frac{{xy}+{yz}+{zx}}{{xyz}}\right)=\mathrm{0} \\ $$
Answered by nimnim last updated on 09/Sep/20
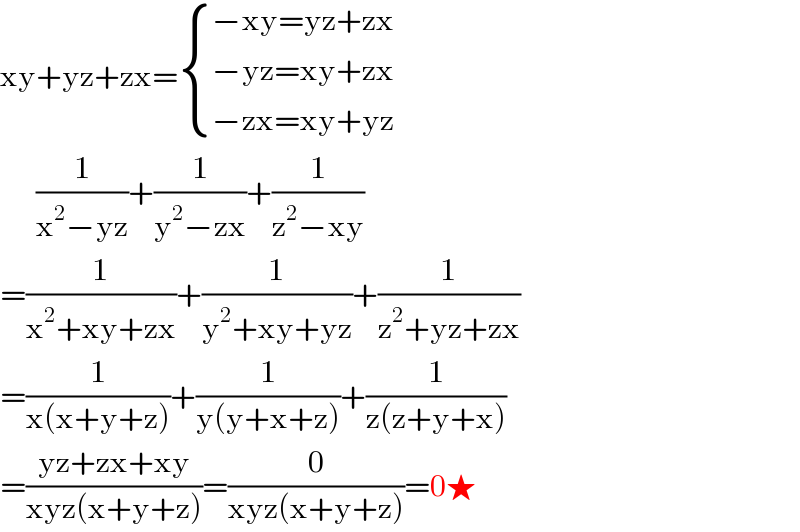
$$\mathrm{xy}+\mathrm{yz}+\mathrm{zx}=\begin{cases}{−\mathrm{xy}=\mathrm{yz}+\mathrm{zx}}\\{−\mathrm{yz}=\mathrm{xy}+\mathrm{zx}}\\{−\mathrm{zx}=\mathrm{xy}+\mathrm{yz}}\end{cases} \\ $$$$\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} −\mathrm{yz}}+\frac{\mathrm{1}}{\mathrm{y}^{\mathrm{2}} −\mathrm{zx}}+\frac{\mathrm{1}}{\mathrm{z}^{\mathrm{2}} −\mathrm{xy}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} +\mathrm{xy}+\mathrm{zx}}+\frac{\mathrm{1}}{\mathrm{y}^{\mathrm{2}} +\mathrm{xy}+\mathrm{yz}}+\frac{\mathrm{1}}{\mathrm{z}^{\mathrm{2}} +\mathrm{yz}+\mathrm{zx}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{x}\left(\mathrm{x}+\mathrm{y}+\mathrm{z}\right)}+\frac{\mathrm{1}}{\mathrm{y}\left(\mathrm{y}+\mathrm{x}+\mathrm{z}\right)}+\frac{\mathrm{1}}{\mathrm{z}\left(\mathrm{z}+\mathrm{y}+\mathrm{x}\right)} \\ $$$$=\frac{\mathrm{yz}+\mathrm{zx}+\mathrm{xy}}{\mathrm{xyz}\left(\mathrm{x}+\mathrm{y}+\mathrm{z}\right)}=\frac{\mathrm{0}}{\mathrm{xyz}\left(\mathrm{x}+\mathrm{y}+\mathrm{z}\right)}=\mathrm{0}\bigstar \\ $$
