
Question Number 5855 by sanusihammed last updated on 01/Jun/16

$${If}\:\:\:{xy}^{\mathrm{3}\:} \:=\:\:{sin}\left({xy}\right) \\ $$$$ \\ $$$${find}\:\:\:\:\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} } \\ $$$$ \\ $$$${Please}\:{i}\:{need}\:{help}.\:{thanks}\:{for}\:{your}\:{effort} \\ $$
Answered by 123456 last updated on 02/Jun/16
![xy^3 =sin(xy) ((d(xy^3 ))/dx)=((d[sin(xy)])/dx) (dx/dx)y^3 +x((d(y^3 ))/dx)=((d[sin(xy)])/(d(xy)))∙((d(xy))/dx) y^3 +x((d(y^3 ))/dy)∙(dy/dx)=cos(xy)∙((dx/dx)y+x(dy/dx)) y^3 +3xy^2 (dy/dx)=cos(xy)(y+x(dy/dx)) y^3 +3xy^2 (dy/dx)=cos(xy)y+cos(xy)x(dy/dx) [3xy^2 −cos(xy)x](dy/dx)=cos(xy)y−y^3 (dy/dx)=((cos(xy)y−y^3 )/(3xy^2 −cos(xy)x)) continue](Q5862.png)
$${xy}^{\mathrm{3}} =\mathrm{sin}\left({xy}\right) \\ $$$$\frac{{d}\left({xy}^{\mathrm{3}} \right)}{{dx}}=\frac{{d}\left[\mathrm{sin}\left({xy}\right)\right]}{{dx}} \\ $$$$\frac{{dx}}{{dx}}{y}^{\mathrm{3}} +{x}\frac{{d}\left({y}^{\mathrm{3}} \right)}{{dx}}=\frac{{d}\left[\mathrm{sin}\left({xy}\right)\right]}{{d}\left({xy}\right)}\centerdot\frac{{d}\left({xy}\right)}{{dx}} \\ $$$${y}^{\mathrm{3}} +{x}\frac{{d}\left({y}^{\mathrm{3}} \right)}{{dy}}\centerdot\frac{{dy}}{{dx}}=\mathrm{cos}\left({xy}\right)\centerdot\left(\frac{{dx}}{{dx}}{y}+{x}\frac{{dy}}{{dx}}\right) \\ $$$${y}^{\mathrm{3}} +\mathrm{3}{xy}^{\mathrm{2}} \frac{{dy}}{{dx}}=\mathrm{cos}\left({xy}\right)\left({y}+{x}\frac{{dy}}{{dx}}\right) \\ $$$${y}^{\mathrm{3}} +\mathrm{3}{xy}^{\mathrm{2}} \frac{{dy}}{{dx}}=\mathrm{cos}\left({xy}\right){y}+\mathrm{cos}\left({xy}\right){x}\frac{{dy}}{{dx}} \\ $$$$\left[\mathrm{3}{xy}^{\mathrm{2}} −\mathrm{cos}\left({xy}\right){x}\right]\frac{{dy}}{{dx}}=\mathrm{cos}\left({xy}\right){y}−{y}^{\mathrm{3}} \\ $$$$\frac{{dy}}{{dx}}=\frac{\mathrm{cos}\left({xy}\right){y}−{y}^{\mathrm{3}} }{\mathrm{3}{xy}^{\mathrm{2}} −\mathrm{cos}\left({xy}\right){x}} \\ $$$$\mathrm{continue} \\ $$
Commented by sanusihammed last updated on 02/Jun/16
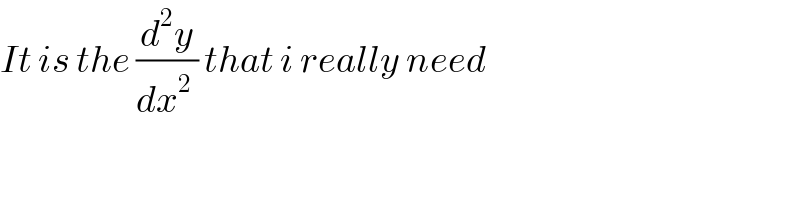
$${It}\:{is}\:{the}\:\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} \:}\:{that}\:{i}\:{really}\:{need} \\ $$
Answered by Yozzii last updated on 02/Jun/16

$${xy}^{\mathrm{3}} ={sin}\left({xy}\right) \\ $$$${Implicit}\:{differentiation}\Rightarrow{y}^{\mathrm{3}} +\mathrm{3}{xy}^{\mathrm{2}} {y}'=\left({xy}'+{y}\right){cos}\left({xy}\right)\Rightarrow{y}'=\frac{{y}^{\mathrm{3}} −{ycos}\left({xy}\right)}{{x}\left({cos}\left({xy}\right)−\mathrm{3}{y}^{\mathrm{2}} \right)}=\frac{{y}\left({y}^{\mathrm{2}} −{cos}\left({xy}\right)\right)}{{x}\left({cos}\left({xy}\right)−\mathrm{3}{y}^{\mathrm{2}} \right)} \\ $$$${Implicit}\:{differentiation}\:{again}\Rightarrow\mathrm{3}{y}^{\mathrm{2}} {y}^{'} +\mathrm{3}{xy}^{\mathrm{2}} {y}''+\left(\mathrm{3}{y}^{\mathrm{2}} +\mathrm{6}{xyy}^{'} \right){y}^{'} \\ $$$$=\left({xy}''+{y}'+{y}'\right){cos}\left({xy}\right)−\left({xy}'+{y}\right)^{\mathrm{2}} {sin}\left({xy}\right) \\ $$$$\mathrm{3}{xy}^{\mathrm{2}} {y}''+\mathrm{6}{yy}'\left({y}+{xy}'\right)={xy}''{cos}\left({xy}\right)+\mathrm{2}{y}'{cos}\left({xy}\right)−\left({xy}'+{y}\right)^{\mathrm{2}} {sin}\left({xy}\right) \\ $$$${x}\left(\mathrm{3}{y}^{\mathrm{2}} −{cos}\left({xy}\right)\right){y}''={y}'\left(\mathrm{2}{cos}\left({xy}\right)−\mathrm{6}{y}\left({y}+{xy}'\right)\right)−\left({xy}'+{y}\right)^{\mathrm{2}} {sin}\left({xy}\right) \\ $$$${y}''=\frac{{y}'\left(\mathrm{2}{cos}\left({xy}\right)−\mathrm{6}{y}\left({y}+{xy}'\right)\right)−{xy}^{\mathrm{3}} \left({xy}'+{y}\right)^{\mathrm{2}} }{{x}\left(\mathrm{3}{y}^{\mathrm{2}} −{cos}\left({xy}\right)\right)} \\ $$$${Let}\:{u}={x}\left(\mathrm{3}{y}^{\mathrm{2}} −{cos}\left({xy}\right)\right),{v}={y}\left({y}^{\mathrm{2}} −{cos}\left({xy}\right)\right) \\ $$$$\therefore{y}'=\frac{{v}}{{u}} \\ $$$$ \\ $$$${y}''=\frac{\frac{{v}}{{u}}\left(\mathrm{2}{cos}\left({xy}\right)−\mathrm{6}{y}\left({y}+{x}\frac{{v}}{{u}}\right)\right)−{xy}^{\mathrm{3}} \left(\frac{{xv}}{{u}}+{y}\right)^{\mathrm{2}} }{{u}} \\ $$$${y}''=\frac{{v}\left(\mathrm{2}{ucos}\left({xy}\right)−\mathrm{6}{y}\left({yu}+{xv}\right)\right)−{xy}^{\mathrm{3}} \left({xv}+{yu}\right)^{\mathrm{2}} }{{u}^{\mathrm{3}} } \\ $$$${y}''=\frac{\mathrm{2}{vucos}\left({xy}\right)−\mathrm{6}{yv}\left({yu}+{xv}\right)−{xy}^{\mathrm{3}} \left({xv}+{yu}\right)^{\mathrm{2}} }{{u}^{\mathrm{3}} } \\ $$$${xv}+{yu}={xy}\left({y}^{\mathrm{2}} −{cos}\left({xy}\right)\right)+{yx}\left(\mathrm{3}{y}^{\mathrm{2}} −{cos}\left({xy}\right)\right) \\ $$$${xv}+{yu}=\mathrm{2}{xy}\left(\mathrm{2}{y}^{\mathrm{2}} −{cos}\left({xy}\right)\right) \\ $$$$ \\ $$$${y}''=\frac{\mathrm{2}{y}\left({y}^{\mathrm{2}} −{cos}\left({xy}\right)\right)\left(\mathrm{3}{y}^{\mathrm{2}} −{cos}\left({xy}\right)\right){cos}\left({xy}\right)−\mathrm{12}{y}^{\mathrm{3}} \left(\mathrm{2}{y}^{\mathrm{2}} −{cos}\left({xy}\right)\right)\left({y}^{\mathrm{2}} −{cos}\left({xy}\right)\right)−\mathrm{4}{x}^{\mathrm{2}} {y}^{\mathrm{5}} \left(\mathrm{2}{y}^{\mathrm{2}} −{cos}\left({xy}\right)\right)^{\mathrm{2}} }{{x}^{\mathrm{2}} \left(\mathrm{3}{y}^{\mathrm{2}} −{cos}\left({xy}\right)\right)^{\mathrm{3}} } \\ $$
Commented by sanusihammed last updated on 02/Jun/16

$${Thanks}\:{so}\:{much} \\ $$
