
Question Number 207197 by hardmath last updated on 09/May/24
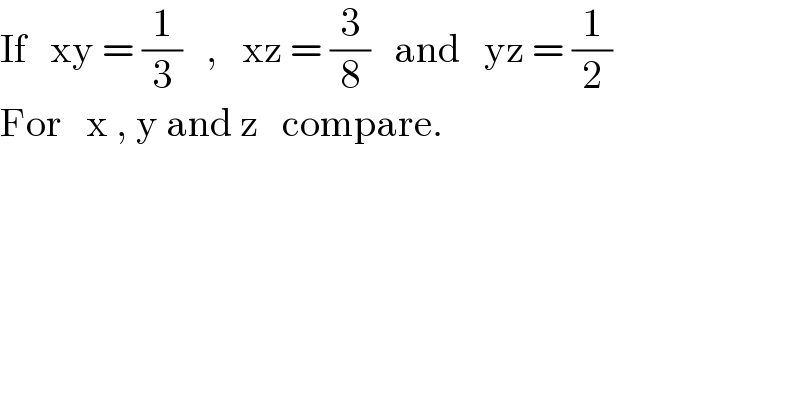
$$\mathrm{If}\:\:\:\mathrm{xy}\:=\:\frac{\mathrm{1}}{\mathrm{3}}\:\:\:,\:\:\:\mathrm{xz}\:=\:\frac{\mathrm{3}}{\mathrm{8}}\:\:\:\mathrm{and}\:\:\:\mathrm{yz}\:=\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{For}\:\:\:\mathrm{x}\:,\:\mathrm{y}\:\mathrm{and}\:\mathrm{z}\:\:\:\mathrm{compare}. \\ $$
Answered by A5T last updated on 09/May/24
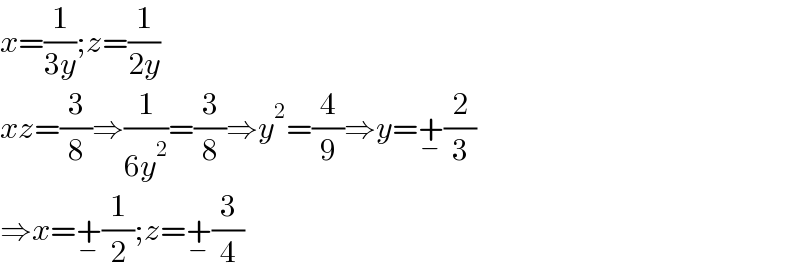
$${x}=\frac{\mathrm{1}}{\mathrm{3}{y}};{z}=\frac{\mathrm{1}}{\mathrm{2}{y}} \\ $$$${xz}=\frac{\mathrm{3}}{\mathrm{8}}\Rightarrow\frac{\mathrm{1}}{\mathrm{6}{y}^{\mathrm{2}} }=\frac{\mathrm{3}}{\mathrm{8}}\Rightarrow{y}^{\mathrm{2}} =\frac{\mathrm{4}}{\mathrm{9}}\Rightarrow{y}=\underset{−} {+}\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\Rightarrow{x}=\underset{−} {+}\frac{\mathrm{1}}{\mathrm{2}};{z}=\underset{−} {+}\frac{\mathrm{3}}{\mathrm{4}} \\ $$
Answered by mr W last updated on 09/May/24
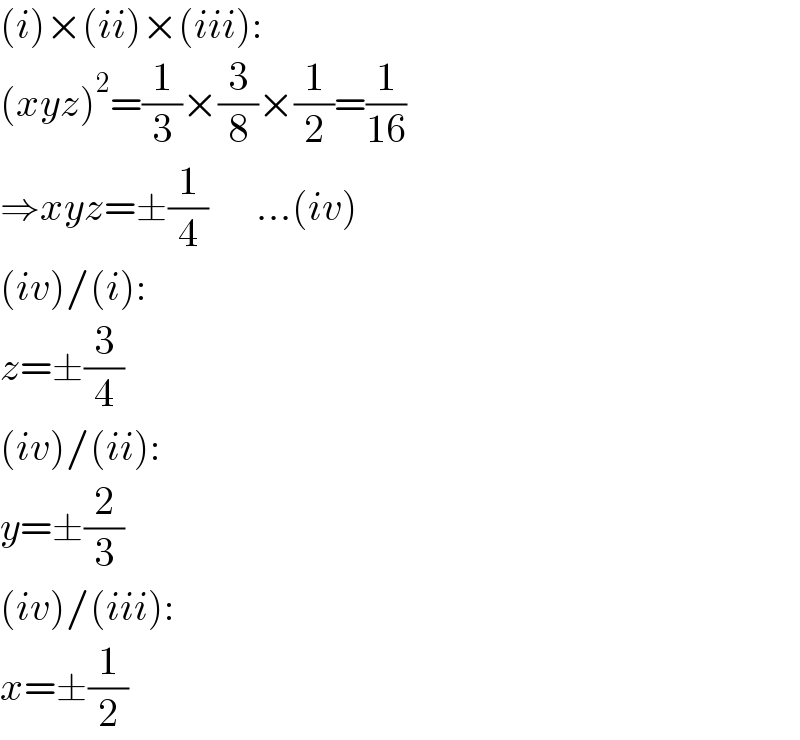
$$\left({i}\right)×\left({ii}\right)×\left({iii}\right): \\ $$$$\left({xyz}\right)^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{3}}×\frac{\mathrm{3}}{\mathrm{8}}×\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{16}} \\ $$$$\Rightarrow{xyz}=\pm\frac{\mathrm{1}}{\mathrm{4}}\:\:\:\:\:\:...\left({iv}\right) \\ $$$$\left({iv}\right)/\left({i}\right): \\ $$$${z}=\pm\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\left({iv}\right)/\left({ii}\right): \\ $$$${y}=\pm\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\left({iv}\right)/\left({iii}\right): \\ $$$${x}=\pm\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by hardmath last updated on 09/May/24
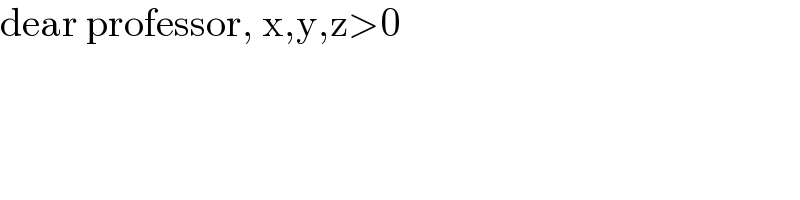
$$\mathrm{dear}\:\mathrm{professor},\:\mathrm{x},\mathrm{y},\mathrm{z}>\mathrm{0} \\ $$
Commented by mr W last updated on 09/May/24
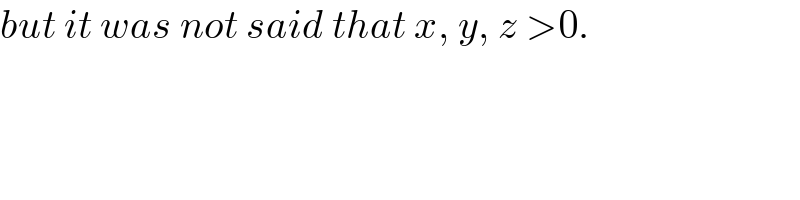
$${but}\:{it}\:{was}\:{not}\:{said}\:{that}\:{x},\:{y},\:{z}\:>\mathrm{0}. \\ $$
Commented by mr W last updated on 09/May/24
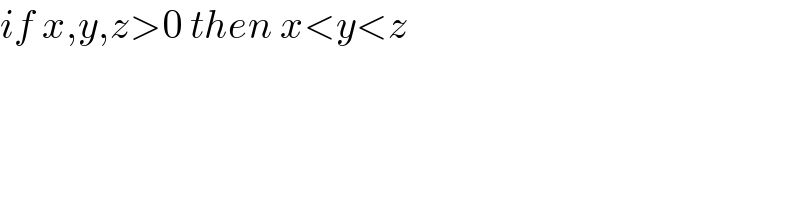
$${if}\:{x},{y},{z}>\mathrm{0}\:{then}\:{x}<{y}<{z} \\ $$
Commented by hardmath last updated on 09/May/24
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{dear}\:\mathrm{professor} \\ $$
