
Question Number 112998 by Aina Samuel Temidayo last updated on 10/Sep/20
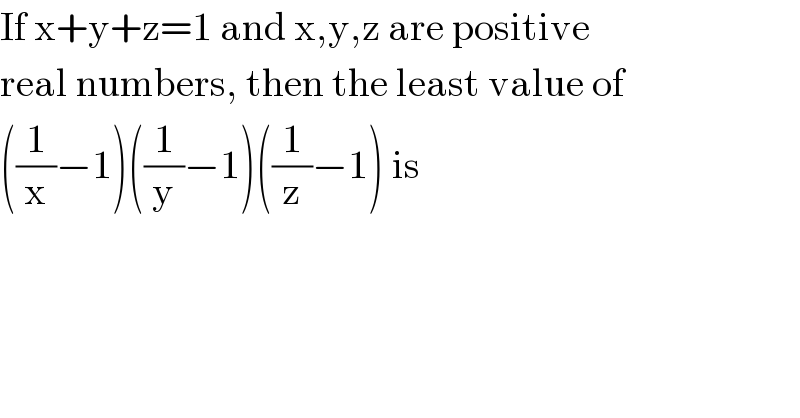
$$\mathrm{If}\:\mathrm{x}+\mathrm{y}+\mathrm{z}=\mathrm{1}\:\mathrm{and}\:\mathrm{x},\mathrm{y},\mathrm{z}\:\mathrm{are}\:\mathrm{positive} \\ $$$$\mathrm{real}\:\mathrm{numbers},\:\mathrm{then}\:\mathrm{the}\:\mathrm{least}\:\mathrm{value}\:\mathrm{of} \\ $$$$\left(\frac{\mathrm{1}}{\mathrm{x}}−\mathrm{1}\right)\left(\frac{\mathrm{1}}{\mathrm{y}}−\mathrm{1}\right)\left(\frac{\mathrm{1}}{\mathrm{z}}−\mathrm{1}\right)\:\mathrm{is}\: \\ $$
Answered by MJS_new last updated on 11/Sep/20
![z=1−x−y ⇒ −(((x−1)(x+y)(y−1))/(x(x+y−1)y)) (d/dy)[−(((x−1)(x+y)(y−1))/(x(x+y−1)y))]=0 −(((x−1)(x+2y−1))/((x+y−1)^2 y^2 ))=0 ⇒ y=((1−x)/2) ⇒ −(((x+1)^2 )/(x(x−1))) (d/dx)[−(((x+1)^2 )/(x(x−1)))]=0 (((x+1)(3x−1))/(x^2 (x−1)^2 ))=0 ⇒ x=y=z=(1/3) ⇒ minimum value is 8](Q113258.png)
$${z}=\mathrm{1}−{x}−{y} \\ $$$$\Rightarrow\:−\frac{\left({x}−\mathrm{1}\right)\left({x}+{y}\right)\left({y}−\mathrm{1}\right)}{{x}\left({x}+{y}−\mathrm{1}\right){y}} \\ $$$$\frac{{d}}{{dy}}\left[−\frac{\left({x}−\mathrm{1}\right)\left({x}+{y}\right)\left({y}−\mathrm{1}\right)}{{x}\left({x}+{y}−\mathrm{1}\right){y}}\right]=\mathrm{0} \\ $$$$−\frac{\left({x}−\mathrm{1}\right)\left({x}+\mathrm{2}{y}−\mathrm{1}\right)}{\left({x}+{y}−\mathrm{1}\right)^{\mathrm{2}} {y}^{\mathrm{2}} }=\mathrm{0}\:\Rightarrow\:{y}=\frac{\mathrm{1}−{x}}{\mathrm{2}} \\ $$$$\Rightarrow\:−\frac{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }{{x}\left({x}−\mathrm{1}\right)} \\ $$$$\frac{{d}}{{dx}}\left[−\frac{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }{{x}\left({x}−\mathrm{1}\right)}\right]=\mathrm{0} \\ $$$$\frac{\left({x}+\mathrm{1}\right)\left(\mathrm{3}{x}−\mathrm{1}\right)}{{x}^{\mathrm{2}} \left({x}−\mathrm{1}\right)^{\mathrm{2}} }=\mathrm{0}\:\Rightarrow\:{x}={y}={z}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\Rightarrow\:\mathrm{minimum}\:\mathrm{value}\:\mathrm{is}\:\mathrm{8} \\ $$
