
Question Number 150303 by mathdanisur last updated on 10/Aug/21
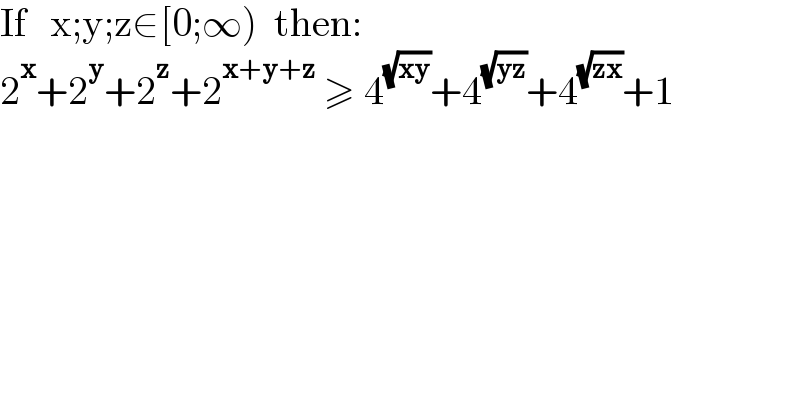
$$\mathrm{If}\:\:\:\mathrm{x};\mathrm{y};\mathrm{z}\in\left[\mathrm{0};\infty\right)\:\:\mathrm{then}: \\ $$$$\mathrm{2}^{\boldsymbol{\mathrm{x}}} +\mathrm{2}^{\boldsymbol{\mathrm{y}}} +\mathrm{2}^{\boldsymbol{\mathrm{z}}} +\mathrm{2}^{\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{y}}+\boldsymbol{\mathrm{z}}} \:\geqslant\:\mathrm{4}^{\sqrt{\boldsymbol{\mathrm{xy}}}} +\mathrm{4}^{\sqrt{\boldsymbol{\mathrm{yz}}}} +\mathrm{4}^{\sqrt{\boldsymbol{\mathrm{zx}}}} +\mathrm{1} \\ $$
Answered by aleks041103 last updated on 11/Aug/21
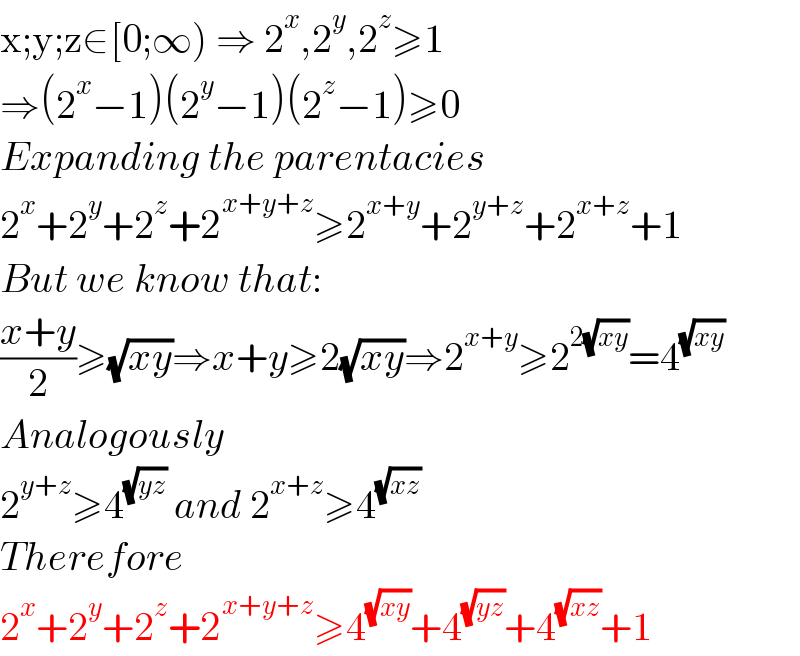
$$\mathrm{x};\mathrm{y};\mathrm{z}\in\left[\mathrm{0};\infty\right)\:\Rightarrow\:\mathrm{2}^{{x}} ,\mathrm{2}^{{y}} ,\mathrm{2}^{{z}} \geqslant\mathrm{1} \\ $$$$\Rightarrow\left(\mathrm{2}^{{x}} −\mathrm{1}\right)\left(\mathrm{2}^{{y}} −\mathrm{1}\right)\left(\mathrm{2}^{{z}} −\mathrm{1}\right)\geqslant\mathrm{0} \\ $$$${Expanding}\:{the}\:{parentacies} \\ $$$$\mathrm{2}^{{x}} +\mathrm{2}^{{y}} +\mathrm{2}^{{z}} +\mathrm{2}^{{x}+{y}+{z}} \geqslant\mathrm{2}^{{x}+{y}} +\mathrm{2}^{{y}+{z}} +\mathrm{2}^{{x}+{z}} +\mathrm{1} \\ $$$${But}\:{we}\:{know}\:{that}: \\ $$$$\frac{{x}+{y}}{\mathrm{2}}\geqslant\sqrt{{xy}}\Rightarrow{x}+{y}\geqslant\mathrm{2}\sqrt{{xy}}\Rightarrow\mathrm{2}^{{x}+{y}} \geqslant\mathrm{2}^{\mathrm{2}\sqrt{{xy}}} =\mathrm{4}^{\sqrt{{xy}}} \\ $$$${Analogously} \\ $$$$\mathrm{2}^{{y}+{z}} \geqslant\mathrm{4}^{\sqrt{{yz}}} \:{and}\:\mathrm{2}^{{x}+{z}} \geqslant\mathrm{4}^{\sqrt{{xz}}} \\ $$$${Therefore} \\ $$$$\mathrm{2}^{{x}} +\mathrm{2}^{{y}} +\mathrm{2}^{{z}} +\mathrm{2}^{{x}+{y}+{z}} \geqslant\mathrm{4}^{\sqrt{{xy}}} +\mathrm{4}^{\sqrt{{yz}}} +\mathrm{4}^{\sqrt{{xz}}} +\mathrm{1} \\ $$
Commented by mathdanisur last updated on 11/Aug/21

$$\mathrm{ThankYou}\:\boldsymbol{\mathrm{S}}\mathrm{er} \\ $$
