
Question Number 63943 by gunawan last updated on 11/Jul/19
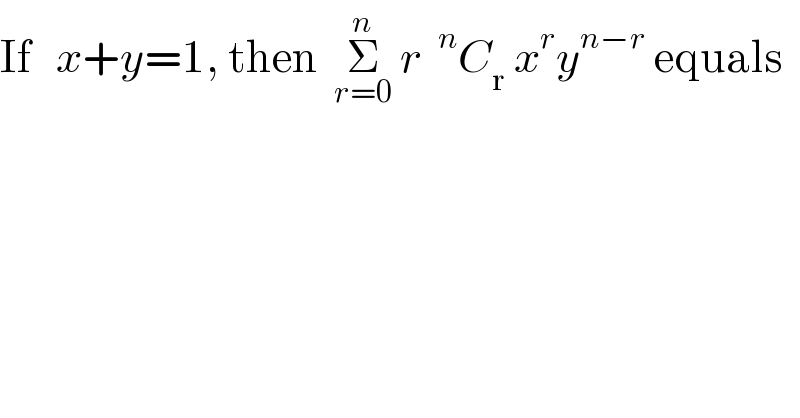
$$\mathrm{If}\:\:\:{x}+{y}=\mathrm{1},\:\mathrm{then}\:\:\underset{{r}=\mathrm{0}} {\overset{{n}} {\sum}}\:{r}\:\:^{{n}} {C}_{\mathrm{r}} \:{x}^{{r}} {y}^{{n}−{r}} \:\mathrm{equals} \\ $$
Commented by mathmax by abdo last updated on 11/Jul/19
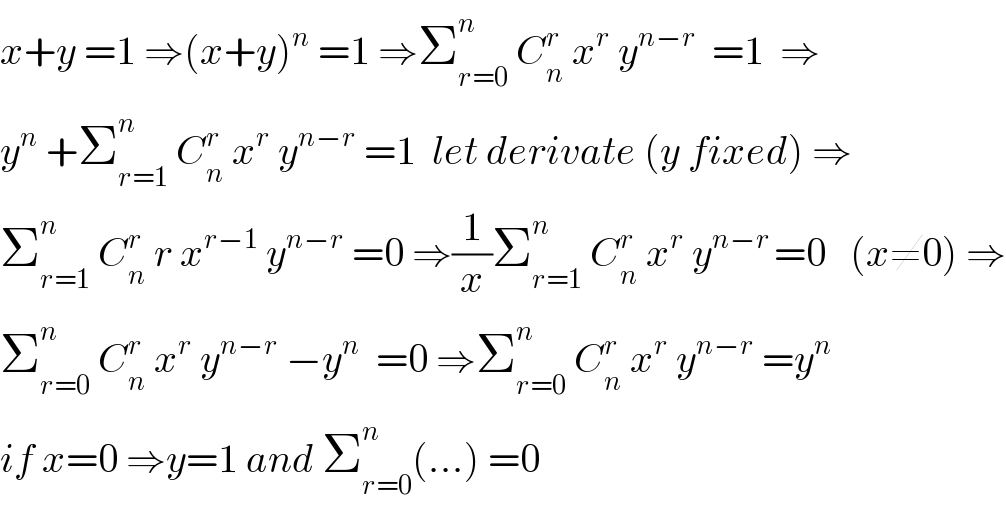
$${x}+{y}\:=\mathrm{1}\:\Rightarrow\left({x}+{y}\right)^{{n}} \:=\mathrm{1}\:\Rightarrow\sum_{{r}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{r}} \:{x}^{{r}} \:{y}^{{n}−{r}} \:\:=\mathrm{1}\:\:\Rightarrow \\ $$$${y}^{{n}} \:+\sum_{{r}=\mathrm{1}} ^{{n}} \:{C}_{{n}} ^{{r}} \:{x}^{{r}} \:{y}^{{n}−{r}} \:=\mathrm{1}\:\:{let}\:{derivate}\:\left({y}\:{fixed}\right)\:\Rightarrow \\ $$$$\sum_{{r}=\mathrm{1}} ^{{n}} \:{C}_{{n}} ^{{r}} \:{r}\:{x}^{{r}−\mathrm{1}} \:{y}^{{n}−{r}} \:=\mathrm{0}\:\Rightarrow\frac{\mathrm{1}}{{x}}\sum_{{r}=\mathrm{1}} ^{{n}} \:{C}_{{n}} ^{{r}} \:{x}^{{r}} \:{y}^{{n}−{r}\:} =\mathrm{0}\:\:\:\left({x}\neq\mathrm{0}\right)\:\Rightarrow \\ $$$$\sum_{{r}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{r}} \:{x}^{{r}} \:{y}^{{n}−{r}} \:−{y}^{{n}} \:\:=\mathrm{0}\:\Rightarrow\sum_{{r}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{r}} \:{x}^{{r}} \:{y}^{{n}−{r}} \:={y}^{{n}} \\ $$$${if}\:{x}=\mathrm{0}\:\Rightarrow{y}=\mathrm{1}\:{and}\:\sum_{{r}=\mathrm{0}} ^{{n}} \left(...\right)\:=\mathrm{0} \\ $$
Answered by mr W last updated on 11/Jul/19
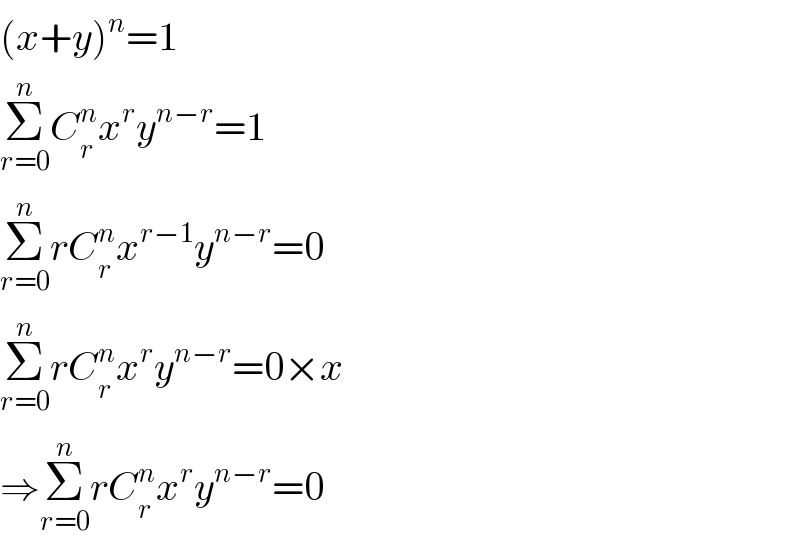
$$\left({x}+{y}\right)^{{n}} =\mathrm{1} \\ $$$$\underset{{r}=\mathrm{0}} {\overset{{n}} {\sum}}{C}_{{r}} ^{{n}} {x}^{{r}} {y}^{{n}−{r}} =\mathrm{1} \\ $$$$\underset{{r}=\mathrm{0}} {\overset{{n}} {\sum}}{rC}_{{r}} ^{{n}} {x}^{{r}−\mathrm{1}} {y}^{{n}−{r}} =\mathrm{0} \\ $$$$\underset{{r}=\mathrm{0}} {\overset{{n}} {\sum}}{rC}_{{r}} ^{{n}} {x}^{{r}} {y}^{{n}−{r}} =\mathrm{0}×{x} \\ $$$$\Rightarrow\underset{{r}=\mathrm{0}} {\overset{{n}} {\sum}}{rC}_{{r}} ^{{n}} {x}^{{r}} {y}^{{n}−{r}} =\mathrm{0} \\ $$
