
Question Number 207175 by MATHEMATICSAM last updated on 08/May/24
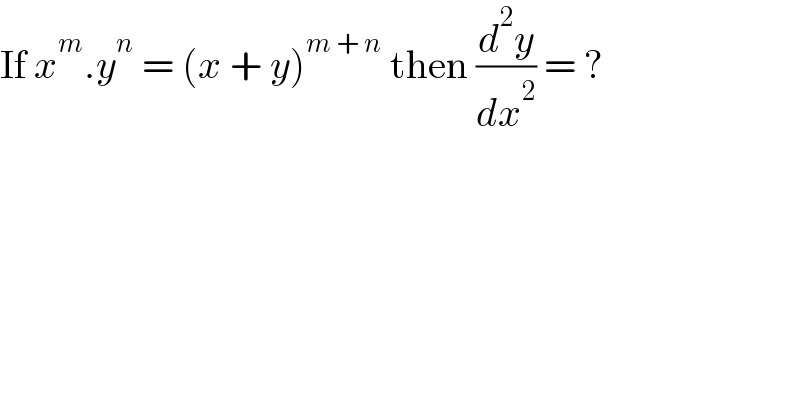
$$\mathrm{If}\:{x}^{{m}} .{y}^{{n}} \:=\:\left({x}\:+\:{y}\right)^{{m}\:+\:{n}} \:\mathrm{then}\:\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\:=\:? \\ $$
Answered by som(math1967) last updated on 08/May/24
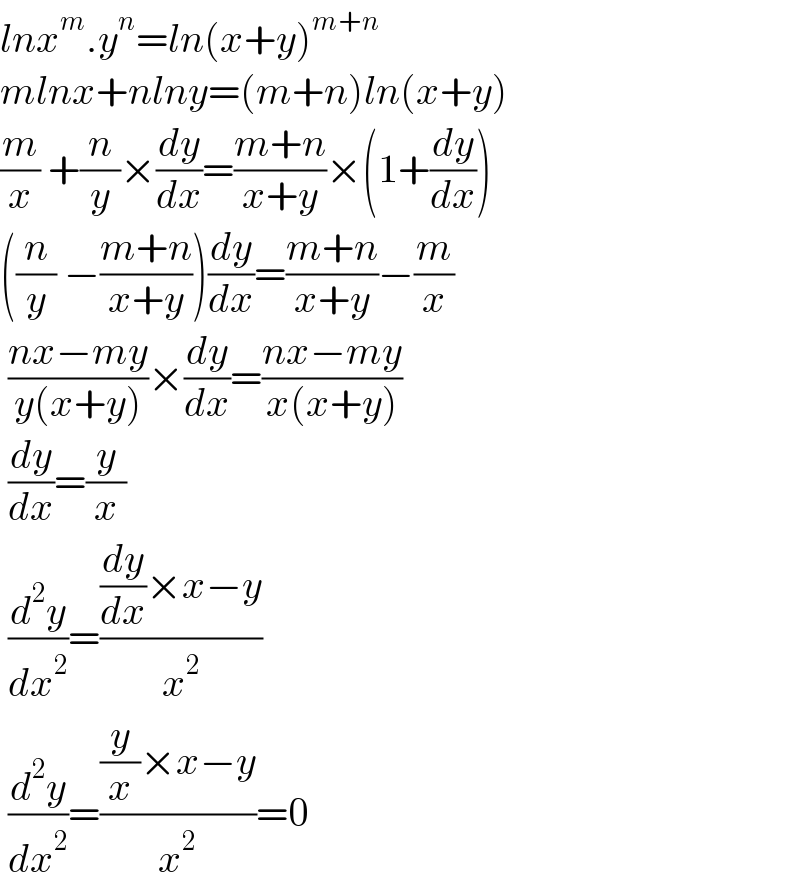
$${lnx}^{{m}} .{y}^{{n}} ={ln}\left({x}+{y}\right)^{{m}+{n}} \\ $$$${mlnx}+{nlny}=\left({m}+{n}\right){ln}\left({x}+{y}\right) \\ $$$$\frac{{m}}{{x}}\:+\frac{{n}}{{y}}×\frac{{dy}}{{dx}}=\frac{{m}+{n}}{{x}+{y}}×\left(\mathrm{1}+\frac{{dy}}{{dx}}\right) \\ $$$$\left(\frac{{n}}{{y}}\:−\frac{{m}+{n}}{{x}+{y}}\right)\frac{{dy}}{{dx}}=\frac{{m}+{n}}{{x}+{y}}−\frac{{m}}{{x}} \\ $$$$\:\frac{{nx}−{my}}{{y}\left({x}+{y}\right)}×\frac{{dy}}{{dx}}=\frac{{nx}−{my}}{{x}\left({x}+{y}\right)} \\ $$$$\:\frac{{dy}}{{dx}}=\frac{{y}}{{x}} \\ $$$$\:\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }=\frac{\frac{{dy}}{{dx}}×{x}−{y}}{{x}^{\mathrm{2}} } \\ $$$$\:\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }=\frac{\frac{{y}}{{x}}×{x}−{y}}{{x}^{\mathrm{2}} }=\mathrm{0} \\ $$
Answered by mr W last updated on 08/May/24
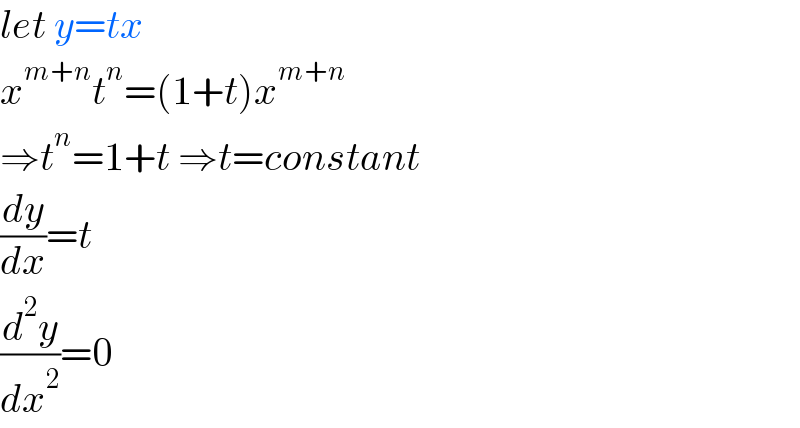
$${let}\:{y}={tx} \\ $$$${x}^{{m}+{n}} {t}^{{n}} =\left(\mathrm{1}+{t}\right){x}^{{m}+{n}} \\ $$$$\Rightarrow{t}^{{n}} =\mathrm{1}+{t}\:\Rightarrow{t}={constant} \\ $$$$\frac{{dy}}{{dx}}={t} \\ $$$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }=\mathrm{0} \\ $$
