Question and Answers Forum

All Questions      Topic List

UNKNOWN Questions

Previous in All Question      Next in All Question      

Previous in UNKNOWN      Next in UNKNOWN      

Question Number 33147 by Ahmad Hajjaj last updated on 11/Apr/18

If x^m occurs in the expansion of (x + (1/x^2 ))^(2n) , the coefficient of x^m is

$$\mathrm{If}\:\:\:{x}^{{m}} \:\:\mathrm{occurs}\:\mathrm{in}\:\mathrm{the}\:\mathrm{expansion}\:\mathrm{of} \\ $$$$\left({x}\:+\:\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)^{\mathrm{2}{n}} ,\:\mathrm{the}\:\mathrm{coefficient}\:\mathrm{of}\:{x}^{{m}} \:\mathrm{is} \\ $$

Commented by prof Abdo imad last updated on 12/Apr/18

we have (x +(1/x^2 ))^(2n) = Σ_(k=0) ^(2n) C_(2n) ^k x^k (x^(−2) )^(2n−k) = Σ_(k=0) ^(2n) C_(2n) ^k x^(k −4n +2k) = Σ_k C_(2n) ^k x^(3k −4n) so if x^m appears in the expansion we get 3k −4n =m⇒ 3k = m +4n ⇒ k =[((m+4n)/3)] and the coefficient is C_(2n) ^([((m+4n)/3)]) .

$${we}\:{have}\:\:\left({x}\:+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)^{\mathrm{2}{n}} \:=\:\sum_{{k}=\mathrm{0}} ^{\mathrm{2}{n}} \:\:\:{C}_{\mathrm{2}{n}} ^{{k}} {x}^{{k}} \:\:\left({x}^{−\mathrm{2}} \right)^{\mathrm{2}{n}−{k}} \\ $$$$=\:\sum_{{k}=\mathrm{0}} ^{\mathrm{2}{n}} \:{C}_{\mathrm{2}{n}} ^{{k}} \:\:{x}^{{k}\:−\mathrm{4}{n}\:+\mathrm{2}{k}} \:\:=\:\sum_{{k}} \:{C}_{\mathrm{2}{n}} ^{{k}} \:\:{x}^{\mathrm{3}{k}\:−\mathrm{4}{n}} \:{so}\:{if}\:{x}^{{m}} \\ $$$${appears}\:{in}\:{the}\:{expansion}\:\:{we}\:{get}\:\mathrm{3}{k}\:−\mathrm{4}{n}\:={m}\Rightarrow \\ $$$$\mathrm{3}{k}\:=\:{m}\:+\mathrm{4}{n}\:\Rightarrow\:{k}\:=\left[\frac{{m}+\mathrm{4}{n}}{\mathrm{3}}\right]\:{and}\:{the}\:{coefficient} \\ $$$${is}\:\:{C}_{\mathrm{2}{n}} ^{\left[\frac{{m}+\mathrm{4}{n}}{\mathrm{3}}\right]} . \\ $$

Answered by Rio Mike last updated on 11/Apr/18

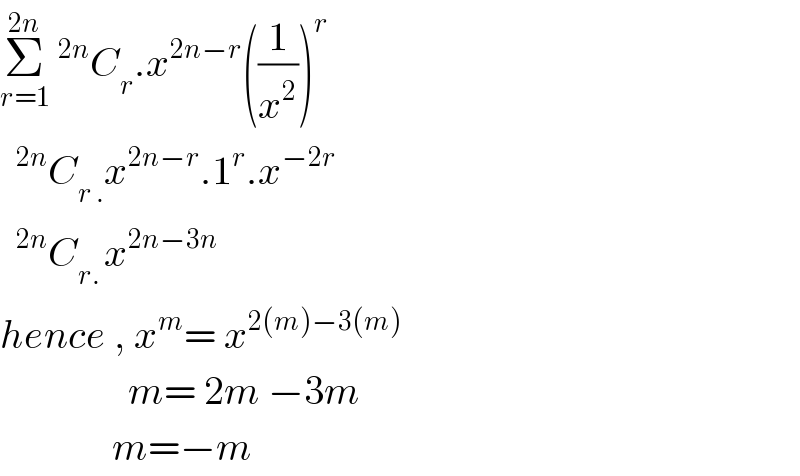
Σ_(r=1) ^(2n) ^(2n) C_r .x^(2n−r) ((1/x^2 ))^r ^(2n) C_(r .) x^(2n−r) .1^r .x^(−2r) ^(2n) C_(r. ) x^(2n−3n) hence , x^m = x^(2(m)−3(m)) m= 2m −3m m=−m

$$\underset{{r}=\mathrm{1}} {\overset{\mathrm{2}{n}} {\sum}}\:^{\mathrm{2}{n}} {C}_{{r}} .{x}^{\mathrm{2}{n}−{r}} \left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)^{{r}} \\ $$$$\:\:^{\mathrm{2}{n}} {C}_{{r}\:.} {x}^{\mathrm{2}{n}−{r}} .\mathrm{1}^{{r}} .{x}^{−\mathrm{2}{r}} \\ $$$$\:\:^{\mathrm{2}{n}} {C}_{{r}.\:} {x}^{\mathrm{2}{n}−\mathrm{3}{n}} \\ $$$${hence}\:,\:{x}^{{m}} =\:{x}^{\mathrm{2}\left({m}\right)−\mathrm{3}\left({m}\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{m}=\:\mathrm{2}{m}\:−\mathrm{3}{m} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:{m}=−{m} \\ $$

Answered by MWSuSon last updated on 25/Apr/20

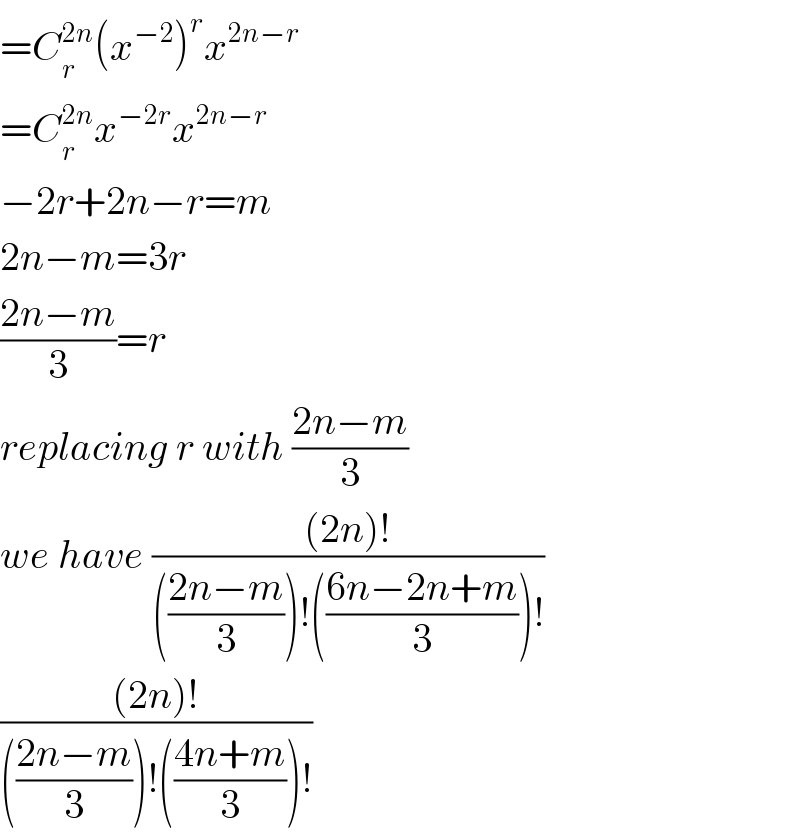
=C_r ^(2n) (x^(−2) )^r x^(2n−r) =C_r ^(2n) x^(−2r) x^(2n−r) −2r+2n−r=m 2n−m=3r ((2n−m)/3)=r replacing r with ((2n−m)/3) we have (((2n)!)/((((2n−m)/3))!(((6n−2n+m)/3))!)) (((2n)!)/((((2n−m)/3))!(((4n+m)/3))!))

$$={C}_{{r}} ^{\mathrm{2}{n}} \left({x}^{−\mathrm{2}} \right)^{{r}} {x}^{\mathrm{2}{n}−{r}} \\ $$$$={C}_{{r}} ^{\mathrm{2}{n}} {x}^{−\mathrm{2}{r}} {x}^{\mathrm{2}{n}−{r}} \\ $$$$−\mathrm{2}{r}+\mathrm{2}{n}−{r}={m} \\ $$$$\mathrm{2}{n}−{m}=\mathrm{3}{r} \\ $$$$\frac{\mathrm{2}{n}−{m}}{\mathrm{3}}={r} \\ $$$${replacing}\:{r}\:{with}\:\frac{\mathrm{2}{n}−{m}}{\mathrm{3}} \\ $$$${we}\:{have}\:\frac{\left(\mathrm{2}{n}\right)!}{\left(\frac{\mathrm{2}{n}−{m}}{\mathrm{3}}\right)!\left(\frac{\mathrm{6}{n}−\mathrm{2}{n}+{m}}{\mathrm{3}}\right)!} \\ $$$$\frac{\left(\mathrm{2}{n}\right)!}{\left(\frac{\mathrm{2}{n}−{m}}{\mathrm{3}}\right)!\left(\frac{\mathrm{4}{n}+{m}}{\mathrm{3}}\right)!} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com