Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 196258 by York12 last updated on 21/Aug/23

If(x_m +iy_m )^(2n+1) =1 , such that m∈{1,2,3,....,2n} ∧ x_m ,y_m ∈R p=Σ_(k=1) ^(2020) [((1−x_k +iy_k )/(1+x_k +iy_k ))] , Find ((p/(43)))

$${If}\left({x}_{{m}} +{iy}_{{m}} \right)^{\mathrm{2}{n}+\mathrm{1}} =\mathrm{1}\:,\:{such}\:{that} \\ $$$${m}\in\left\{\mathrm{1},\mathrm{2},\mathrm{3},....,\mathrm{2}{n}\right\}\:\wedge\:{x}_{{m}} ,{y}_{{m}} \in\mathbb{R} \\ $$$${p}=\underset{{k}=\mathrm{1}} {\overset{\mathrm{2020}} {\sum}}\left[\frac{\mathrm{1}−{x}_{{k}} +{iy}_{{k}} }{\mathrm{1}+{x}_{{k}} +{iy}_{{k}} }\right]\:,\:{Find}\:\left(\frac{{p}}{\mathrm{43}}\right) \\ $$

Commented by York12 last updated on 21/Aug/23

(x_m +iy_m )=e^((2imπ)/(2n+1)) ,m∈{0,......2n} Z_m =e^(2i((mπ)/(2n+1))) ,ia_(k,n) =((2ikπ)/(2n+1)) for all the reste n=1010 Σ_(k=1) ^(2020) ((1−x_k +iy_k )/(1+x_k +iy_k ))=Σ_(k=0) ^(2020) ((1−(x_k −iy_k ))/(1+(x_k +iy_k )))=Σ((1−e^(−ia_k ) )/(1+e^(ia_k ) )) =Σ((e^(ia_k ) −1)/(e^(ia_k ) (1+e^(ia_k ) )))=Σ_k (2/(1+e^(ia_k ) ))−(1/e^(ia_k ) ) ler p(x)=x^(2n+1) −1 ((p′(x))/(p(x)))=Σ_(k=0) ^(2n) (1/(X−e^(ia_k ) ))⇒((p′(−1))/(p(−1)))=−Σ(1/(1+e^(ia_k ) )) ⇒Σ_(k=0) ^(2020) (1/(1+e^(ia_k ) ))=−(((2021))/(−2))=((2021)/2) Σ_(k=0) ^(2020) e^(−ia_k ) =((1−(e^(−i((2π)/(2021))) )^(2021) )/(1−e^(−((i2π)/(2021))) ))=0 P=2.((2021)/2)=2021=43.47 (p/(43))=47

$$ \\ $$$$\left(\mathrm{x}_{\mathrm{m}} +\mathrm{iy}_{\mathrm{m}} \right)=\mathrm{e}^{\frac{\mathrm{2im}\pi}{\mathrm{2n}+\mathrm{1}}} ,\mathrm{m}\in\left\{\mathrm{0},......\mathrm{2n}\right\} \\ $$$$\mathrm{Z}_{\mathrm{m}} =\mathrm{e}^{\mathrm{2i}\frac{\mathrm{m}\pi}{\mathrm{2n}+\mathrm{1}}} ,\mathrm{ia}_{\mathrm{k},\mathrm{n}} =\frac{\mathrm{2ik}\pi}{\mathrm{2n}+\mathrm{1}} \\ $$$$\mathrm{for}\:\mathrm{all}\:\mathrm{the}\:\mathrm{reste}\:\mathrm{n}=\mathrm{1010} \\ $$$$\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{2020}} {\sum}}\frac{\mathrm{1}−\mathrm{x}_{\mathrm{k}} +\mathrm{iy}_{\mathrm{k}} }{\mathrm{1}+\mathrm{x}_{\mathrm{k}} +\mathrm{iy}_{\mathrm{k}} }=\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{2020}} {\sum}}\frac{\mathrm{1}−\left(\mathrm{x}_{\mathrm{k}} −\mathrm{iy}_{\mathrm{k}} \right)}{\mathrm{1}+\left(\mathrm{x}_{\mathrm{k}} +\mathrm{iy}_{\mathrm{k}} \right)}=\Sigma\frac{\mathrm{1}−\mathrm{e}^{−\mathrm{ia}_{\mathrm{k}} } }{\mathrm{1}+\mathrm{e}^{\mathrm{ia}_{\mathrm{k}} } } \\ $$$$=\Sigma\frac{\boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{ia}}_{\boldsymbol{\mathrm{k}}} } −\mathrm{1}}{\mathrm{e}^{\mathrm{ia}_{\mathrm{k}} } \left(\mathrm{1}+\mathrm{e}^{\mathrm{ia}_{\mathrm{k}} } \right)}=\underset{\mathrm{k}} {\sum}\frac{\mathrm{2}}{\mathrm{1}+\mathrm{e}^{\mathrm{ia}_{\mathrm{k}} } }−\frac{\mathrm{1}}{\mathrm{e}^{\mathrm{ia}_{\mathrm{k}} } } \\ $$$$\mathrm{ler}\:\mathrm{p}\left(\mathrm{x}\right)=\mathrm{x}^{\mathrm{2n}+\mathrm{1}} −\mathrm{1} \\ $$$$\frac{\mathrm{p}'\left(\mathrm{x}\right)}{\mathrm{p}\left(\mathrm{x}\right)}=\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{2n}} {\sum}}\frac{\mathrm{1}}{\mathrm{X}−\mathrm{e}^{\mathrm{ia}_{\mathrm{k}} } }\Rightarrow\frac{\mathrm{p}'\left(−\mathrm{1}\right)}{\mathrm{p}\left(−\mathrm{1}\right)}=−\Sigma\frac{\mathrm{1}}{\mathrm{1}+\mathrm{e}^{\mathrm{ia}_{\mathrm{k}} } } \\ $$$$\Rightarrow\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{2020}} {\sum}}\frac{\mathrm{1}}{\mathrm{1}+\mathrm{e}^{\mathrm{ia}_{\mathrm{k}} } }=−\frac{\left(\mathrm{2021}\right)}{−\mathrm{2}}=\frac{\mathrm{2021}}{\mathrm{2}} \\ $$$$\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{2020}} {\sum}}\mathrm{e}^{−\mathrm{ia}_{\mathrm{k}} } =\frac{\mathrm{1}−\left(\mathrm{e}^{−\mathrm{i}\frac{\mathrm{2}\pi}{\mathrm{2021}}} \right)^{\mathrm{2021}} }{\mathrm{1}−\mathrm{e}^{−\frac{\mathrm{i2}\pi}{\mathrm{2021}}} }=\mathrm{0} \\ $$$$\mathrm{P}=\mathrm{2}.\frac{\mathrm{2021}}{\mathrm{2}}=\mathrm{2021}=\mathrm{43}.\mathrm{47} \\ $$$$\frac{\mathrm{p}}{\mathrm{43}}=\mathrm{47} \\ $$$$ \\ $$

Commented by York12 last updated on 21/Aug/23

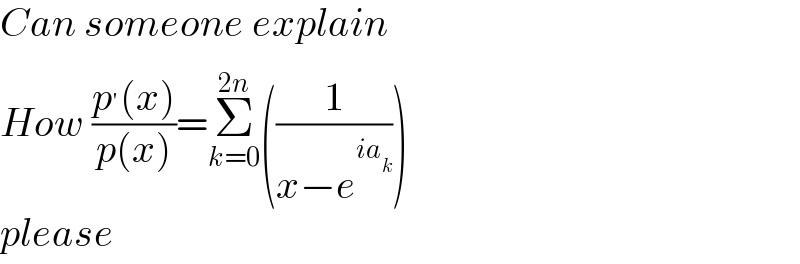
Can someone explain How ((p^′ (x))/(p(x)))=Σ_(k=0) ^(2n) ((1/(x−e^(ia_k ) ))) please

$${Can}\:{someone}\:{explain} \\ $$$${How}\:\frac{{p}^{'} \left({x}\right)}{{p}\left({x}\right)}=\underset{{k}=\mathrm{0}} {\overset{\mathrm{2}{n}} {\sum}}\left(\frac{\mathrm{1}}{{x}−{e}^{{ia}_{{k}} } }\right) \\ $$$${please} \\ $$

Commented by sniper237 last updated on 22/Aug/23

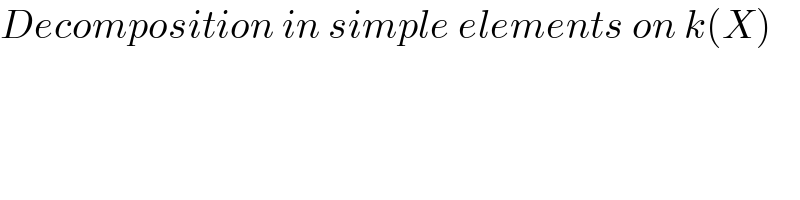
Decomposition in simple elements on k(X)

$${Decomposition}\:{in}\:{simple}\:{elements}\:{on}\:{k}\left({X}\right)\:\: \\ $$

Commented by York12 last updated on 22/Aug/23

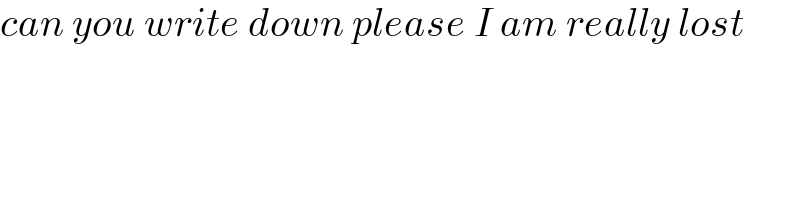
can you write down please I am really lost

$${can}\:{you}\:{write}\:{down}\:{please}\:{I}\:{am}\:{really}\:{lost} \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com