
Question Number 196582 by MATHEMATICSAM last updated on 27/Aug/23
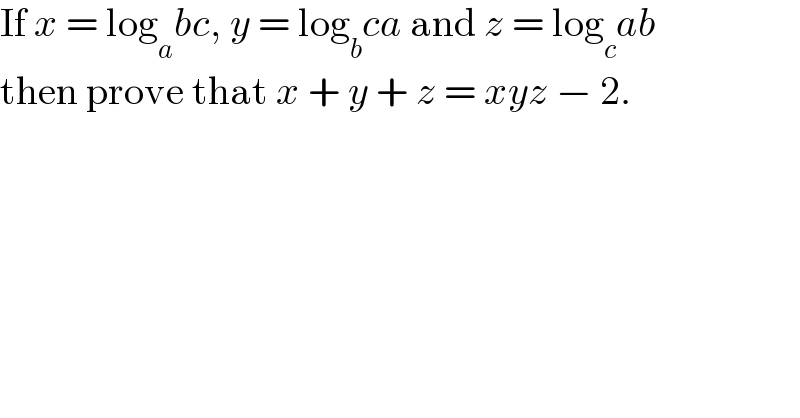
$$\mathrm{If}\:{x}\:=\:\mathrm{log}_{{a}} {bc},\:{y}\:=\:\mathrm{log}_{{b}} {ca}\:\mathrm{and}\:{z}\:=\:\mathrm{log}_{{c}} {ab} \\ $$$$\mathrm{then}\:\mathrm{prove}\:\mathrm{that}\:{x}\:+\:{y}\:+\:{z}\:=\:{xyz}\:−\:\mathrm{2}. \\ $$
Answered by som(math1967) last updated on 27/Aug/23
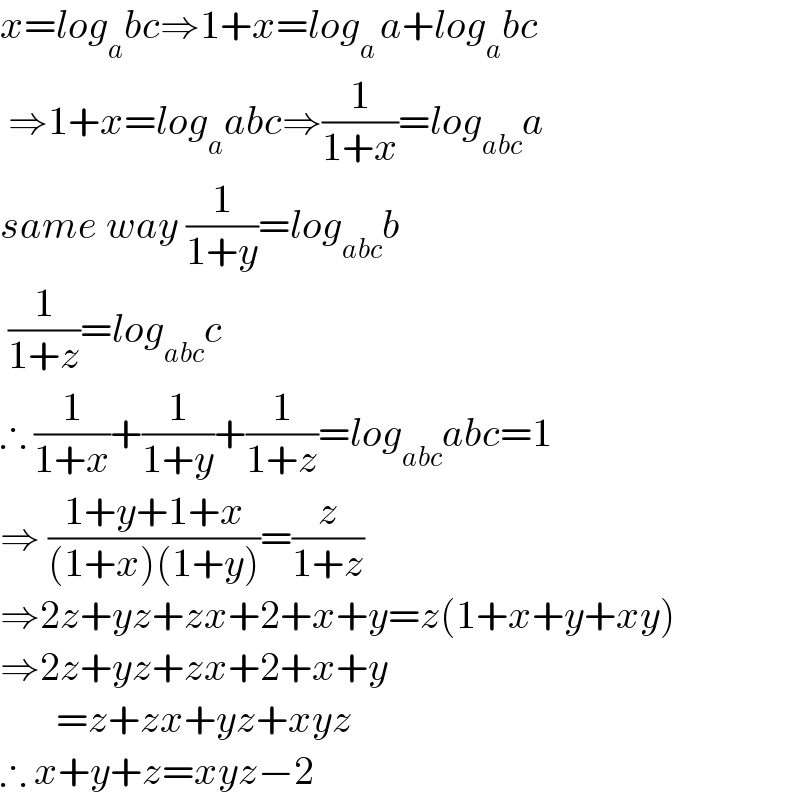
$${x}={log}_{{a}} {bc}\Rightarrow\mathrm{1}+{x}={log}_{{a}\:} {a}+{log}_{{a}} {bc} \\ $$$$\:\Rightarrow\mathrm{1}+{x}={log}_{{a}} {abc}\Rightarrow\frac{\mathrm{1}}{\mathrm{1}+{x}}={log}_{{abc}} {a} \\ $$$${same}\:{way}\:\frac{\mathrm{1}}{\mathrm{1}+{y}}={log}_{{abc}} {b} \\ $$$$\:\frac{\mathrm{1}}{\mathrm{1}+{z}}={log}_{{abc}} {c} \\ $$$$\therefore\:\frac{\mathrm{1}}{\mathrm{1}+{x}}+\frac{\mathrm{1}}{\mathrm{1}+{y}}+\frac{\mathrm{1}}{\mathrm{1}+{z}}={log}_{{abc}} {abc}=\mathrm{1} \\ $$$$\Rightarrow\:\frac{\mathrm{1}+{y}+\mathrm{1}+{x}}{\left(\mathrm{1}+{x}\right)\left(\mathrm{1}+{y}\right)}=\frac{{z}}{\mathrm{1}+{z}} \\ $$$$\Rightarrow\mathrm{2}{z}+{yz}+{zx}+\mathrm{2}+{x}+{y}={z}\left(\mathrm{1}+{x}+{y}+{xy}\right) \\ $$$$\Rightarrow\mathrm{2}{z}+{yz}+{zx}+\mathrm{2}+{x}+{y} \\ $$$$\:\:\:\:\:\:\:={z}+{zx}+{yz}+{xyz} \\ $$$$\therefore\:{x}+{y}+{z}={xyz}−\mathrm{2} \\ $$
