
Question Number 51284 by Tawa1 last updated on 25/Dec/18
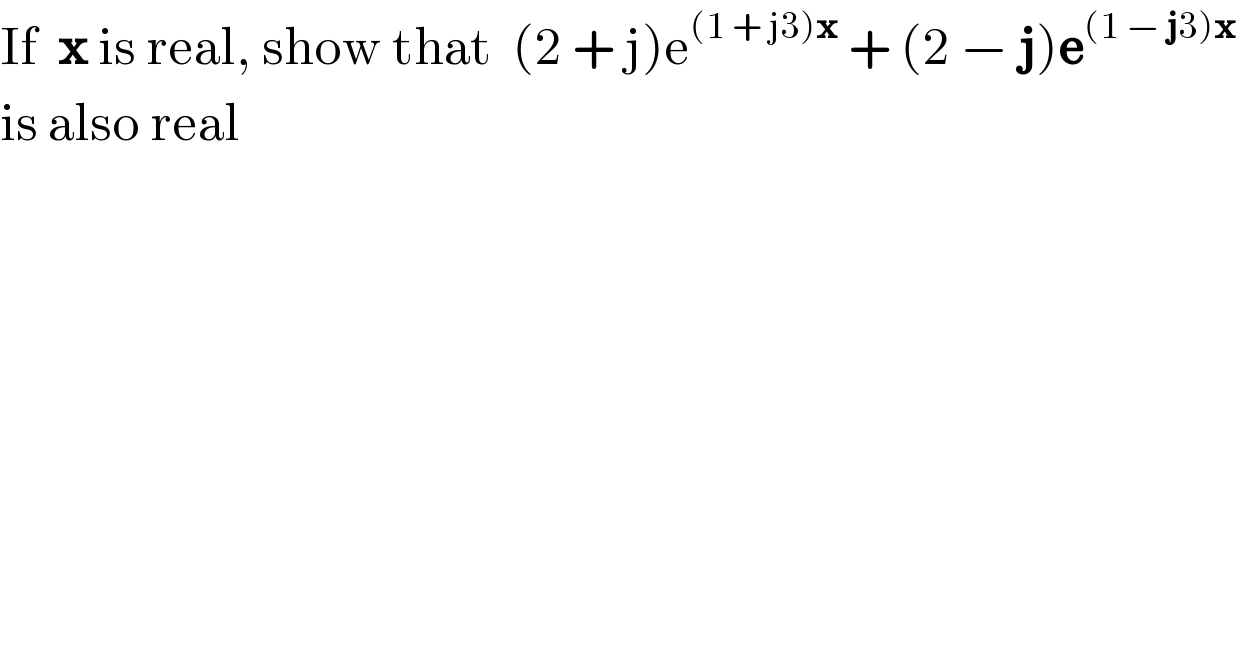
$$\mathrm{If}\:\:\boldsymbol{\mathrm{x}}\:\mathrm{is}\:\mathrm{real},\:\mathrm{show}\:\mathrm{that}\:\:\left(\mathrm{2}\:+\:\mathrm{j}\right)\mathrm{e}^{\left(\mathrm{1}\:+\:\mathrm{j3}\right)\boldsymbol{\mathrm{x}}} \:+\:\left(\mathrm{2}\:−\:\boldsymbol{\mathrm{j}}\right)\boldsymbol{\mathrm{e}}^{\left(\mathrm{1}\:−\:\boldsymbol{\mathrm{j}}\mathrm{3}\right)\boldsymbol{\mathrm{x}}} \\ $$$$\mathrm{is}\:\mathrm{also}\:\mathrm{real} \\ $$
Commented by maxmathsup by imad last updated on 25/Dec/18
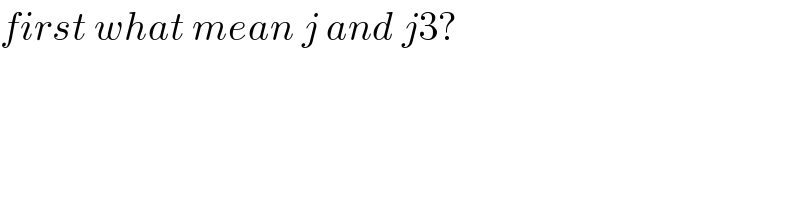
$${first}\:{what}\:{mean}\:{j}\:{and}\:{j}\mathrm{3}? \\ $$$$ \\ $$
Answered by mr W last updated on 25/Dec/18
![2+i=(√5)((2/(√5))+(1/(√5))i)=(√5)(cos α+i sin α) =(√5)e^(αi) with α=tan^(−1) (1/2) 2−i=(√5)((2/(√5))−(1/(√5))i)=(√5)[cos (−α)+i sin (−α)] =(√5)e^(−αi) S=(2+i)e^((1+3i)x) +(2−i)e^((1−3i)x) =(√5)e^(αi) e^((1+3i)x) +(√5)e^(−αi) e^((1−3i)x) =(√5)e^x [e^((3x+α)i) +e^(−(3x+α)i) ] =(√5)e^x [cos (3x+α)+i sin (3x+α)+cos {−(3x+α)}+i sin {−(3x+α)}] =(√5)e^x [cos (3x+α)+i sin (3x+α)+cos (3x+α)−i sin (3x+α)] =(√5)e^x [2cos (3x+α)] =2(√5)e^x cos (3x+α) =2(√5)e^x (cos α cos 3x−sin α sin 3x) =2(√5)e^x ((2/(√5))cos 3x−(1/(√5))sin 3x) =2e^x (2 cos 3x−sin 3x) =real](Q51294.png)
$$\mathrm{2}+{i}=\sqrt{\mathrm{5}}\left(\frac{\mathrm{2}}{\sqrt{\mathrm{5}}}+\frac{\mathrm{1}}{\sqrt{\mathrm{5}}}{i}\right)=\sqrt{\mathrm{5}}\left(\mathrm{cos}\:\alpha+{i}\:\mathrm{sin}\:\alpha\right) \\ $$$$=\sqrt{\mathrm{5}}{e}^{\alpha{i}} \\ $$$${with}\:\alpha=\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{2}−{i}=\sqrt{\mathrm{5}}\left(\frac{\mathrm{2}}{\sqrt{\mathrm{5}}}−\frac{\mathrm{1}}{\sqrt{\mathrm{5}}}{i}\right)=\sqrt{\mathrm{5}}\left[\mathrm{cos}\:\left(−\alpha\right)+{i}\:\mathrm{sin}\:\left(−\alpha\right)\right] \\ $$$$=\sqrt{\mathrm{5}}{e}^{−\alpha{i}} \\ $$$$ \\ $$$${S}=\left(\mathrm{2}+{i}\right){e}^{\left(\mathrm{1}+\mathrm{3}{i}\right){x}} +\left(\mathrm{2}−{i}\right){e}^{\left(\mathrm{1}−\mathrm{3}{i}\right){x}} \\ $$$$=\sqrt{\mathrm{5}}{e}^{\alpha{i}} {e}^{\left(\mathrm{1}+\mathrm{3}{i}\right){x}} +\sqrt{\mathrm{5}}{e}^{−\alpha{i}} {e}^{\left(\mathrm{1}−\mathrm{3}{i}\right){x}} \\ $$$$=\sqrt{\mathrm{5}}{e}^{{x}} \left[{e}^{\left(\mathrm{3}{x}+\alpha\right){i}} +{e}^{−\left(\mathrm{3}{x}+\alpha\right){i}} \right] \\ $$$$=\sqrt{\mathrm{5}}{e}^{{x}} \left[\mathrm{cos}\:\left(\mathrm{3}{x}+\alpha\right)+{i}\:\mathrm{sin}\:\left(\mathrm{3}{x}+\alpha\right)+\mathrm{cos}\:\left\{−\left(\mathrm{3}{x}+\alpha\right)\right\}+{i}\:\mathrm{sin}\:\left\{−\left(\mathrm{3}{x}+\alpha\right)\right\}\right] \\ $$$$=\sqrt{\mathrm{5}}{e}^{{x}} \left[\mathrm{cos}\:\left(\mathrm{3}{x}+\alpha\right)+{i}\:\mathrm{sin}\:\left(\mathrm{3}{x}+\alpha\right)+\mathrm{cos}\:\left(\mathrm{3}{x}+\alpha\right)−{i}\:\mathrm{sin}\:\left(\mathrm{3}{x}+\alpha\right)\right] \\ $$$$=\sqrt{\mathrm{5}}{e}^{{x}} \left[\mathrm{2cos}\:\left(\mathrm{3}{x}+\alpha\right)\right] \\ $$$$=\mathrm{2}\sqrt{\mathrm{5}}{e}^{{x}} \:\mathrm{cos}\:\left(\mathrm{3}{x}+\alpha\right) \\ $$$$=\mathrm{2}\sqrt{\mathrm{5}}{e}^{{x}} \:\left(\mathrm{cos}\:\alpha\:\mathrm{cos}\:\mathrm{3}{x}−\mathrm{sin}\:\alpha\:\mathrm{sin}\:\mathrm{3}{x}\right) \\ $$$$=\mathrm{2}\sqrt{\mathrm{5}}{e}^{{x}} \:\left(\frac{\mathrm{2}}{\sqrt{\mathrm{5}}}\mathrm{cos}\:\mathrm{3}{x}−\frac{\mathrm{1}}{\sqrt{\mathrm{5}}}\mathrm{sin}\:\mathrm{3}{x}\right) \\ $$$$=\mathrm{2}{e}^{{x}} \left(\mathrm{2}\:\mathrm{cos}\:\mathrm{3}{x}−\mathrm{sin}\:\mathrm{3}{x}\right) \\ $$$$={real} \\ $$
Commented by Tawa1 last updated on 25/Dec/18
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
