Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 216253 by MATHEMATICSAM last updated on 01/Feb/25

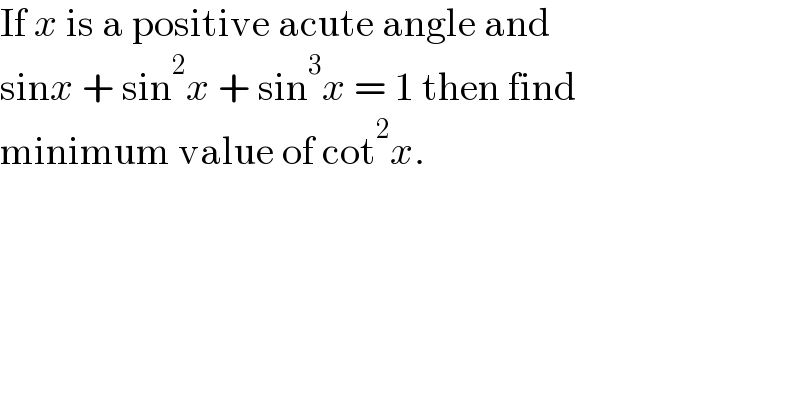
If x is a positive acute angle and sinx + sin^2 x + sin^3 x = 1 then find minimum value of cot^2 x.

$$\mathrm{If}\:{x}\:\mathrm{is}\:\mathrm{a}\:\mathrm{positive}\:\mathrm{acute}\:\mathrm{angle}\:\mathrm{and} \\ $$$$\mathrm{sin}{x}\:+\:\mathrm{sin}^{\mathrm{2}} {x}\:+\:\mathrm{sin}^{\mathrm{3}} {x}\:=\:\mathrm{1}\:\mathrm{then}\:\mathrm{find} \\ $$$$\mathrm{minimum}\:\mathrm{value}\:\mathrm{of}\:\mathrm{cot}^{\mathrm{2}} {x}. \\ $$

Commented by Frix last updated on 03/Feb/25

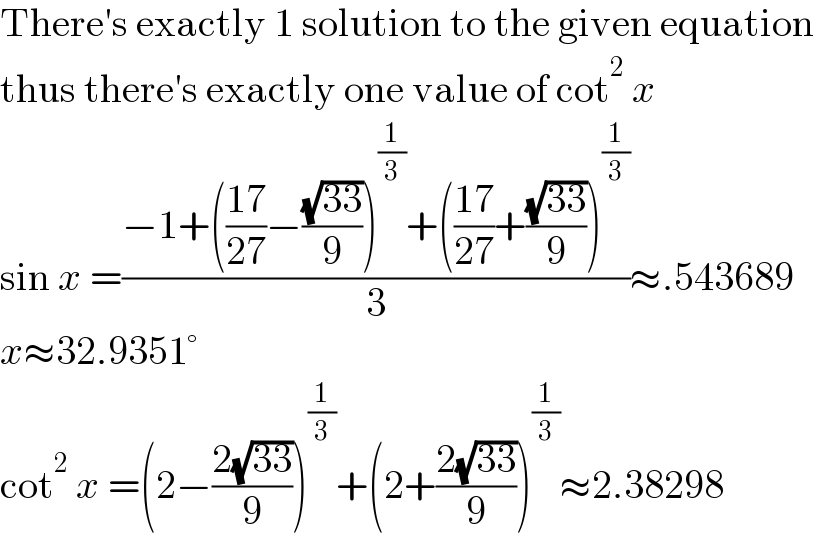
There′s exactly 1 solution to the given equation thus there′s exactly one value of cot^2 x sin x =((−1+(((17)/(27))−((√(33))/9))^(1/3) +(((17)/(27))+((√(33))/9))^(1/3) )/3)≈.543689 x≈32.9351° cot^2 x =(2−((2(√(33)))/9))^(1/3) +(2+((2(√(33)))/9))^(1/3) ≈2.38298

$$\mathrm{There}'\mathrm{s}\:\mathrm{exactly}\:\mathrm{1}\:\mathrm{solution}\:\mathrm{to}\:\mathrm{the}\:\mathrm{given}\:\mathrm{equation} \\ $$$$\mathrm{thus}\:\mathrm{there}'\mathrm{s}\:\mathrm{exactly}\:\mathrm{one}\:\mathrm{value}\:\mathrm{of}\:\mathrm{cot}^{\mathrm{2}} \:{x} \\ $$$$\mathrm{sin}\:{x}\:=\frac{−\mathrm{1}+\left(\frac{\mathrm{17}}{\mathrm{27}}−\frac{\sqrt{\mathrm{33}}}{\mathrm{9}}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} +\left(\frac{\mathrm{17}}{\mathrm{27}}+\frac{\sqrt{\mathrm{33}}}{\mathrm{9}}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} }{\mathrm{3}}\approx.\mathrm{543689} \\ $$$${x}\approx\mathrm{32}.\mathrm{9351}° \\ $$$$\mathrm{cot}^{\mathrm{2}} \:{x}\:=\left(\mathrm{2}−\frac{\mathrm{2}\sqrt{\mathrm{33}}}{\mathrm{9}}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} +\left(\mathrm{2}+\frac{\mathrm{2}\sqrt{\mathrm{33}}}{\mathrm{9}}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \approx\mathrm{2}.\mathrm{38298} \\ $$

Answered by AntonCWX last updated on 03/Feb/25

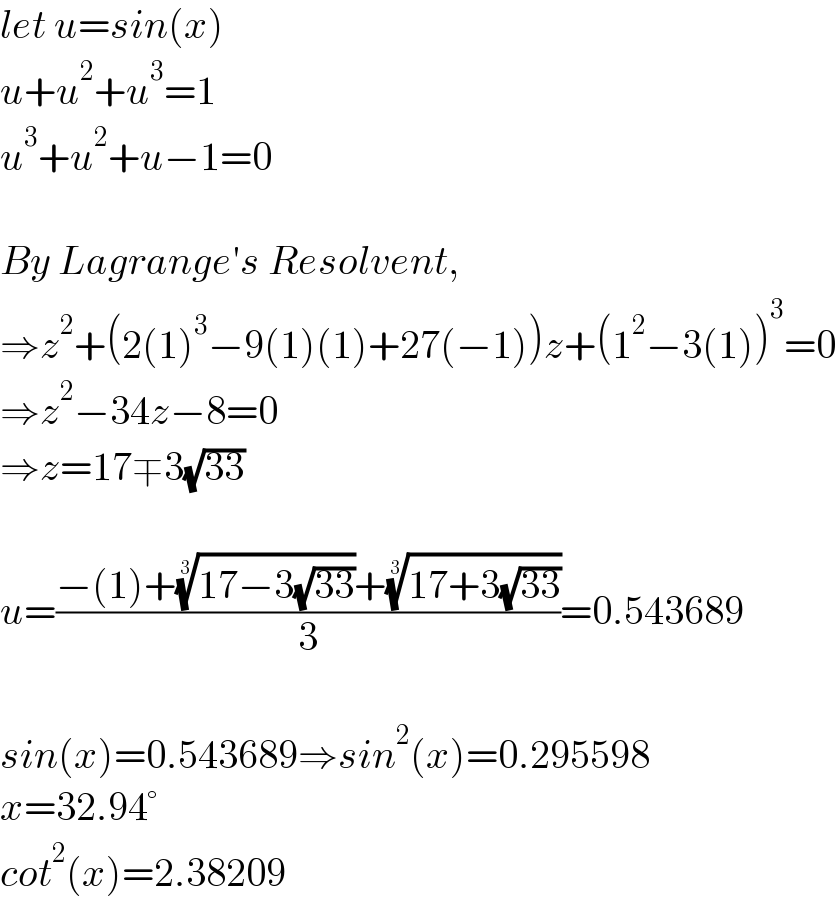
let u=sin(x) u+u^2 +u^3 =1 u^3 +u^2 +u−1=0 By Lagrange′s Resolvent, ⇒z^2 +(2(1)^3 −9(1)(1)+27(−1))z+(1^2 −3(1))^3 =0 ⇒z^2 −34z−8=0 ⇒z=17∓3(√(33)) u=((−(1)+((17−3(√(33))))^(1/3) +((17+3(√(33))))^(1/3) )/3)=0.543689 sin(x)=0.543689⇒sin^2 (x)=0.295598 x=32.94° cot^2 (x)=2.38209

$${let}\:{u}={sin}\left({x}\right) \\ $$$${u}+{u}^{\mathrm{2}} +{u}^{\mathrm{3}} =\mathrm{1} \\ $$$${u}^{\mathrm{3}} +{u}^{\mathrm{2}} +{u}−\mathrm{1}=\mathrm{0} \\ $$$$ \\ $$$${By}\:{Lagrange}'{s}\:{Resolvent}, \\ $$$$\Rightarrow{z}^{\mathrm{2}} +\left(\mathrm{2}\left(\mathrm{1}\right)^{\mathrm{3}} −\mathrm{9}\left(\mathrm{1}\right)\left(\mathrm{1}\right)+\mathrm{27}\left(−\mathrm{1}\right)\right){z}+\left(\mathrm{1}^{\mathrm{2}} −\mathrm{3}\left(\mathrm{1}\right)\right)^{\mathrm{3}} =\mathrm{0} \\ $$$$\Rightarrow{z}^{\mathrm{2}} −\mathrm{34}{z}−\mathrm{8}=\mathrm{0} \\ $$$$\Rightarrow{z}=\mathrm{17}\mp\mathrm{3}\sqrt{\mathrm{33}} \\ $$$$ \\ $$$${u}=\frac{−\left(\mathrm{1}\right)+\sqrt[{\mathrm{3}}]{\mathrm{17}−\mathrm{3}\sqrt{\mathrm{33}}}+\sqrt[{\mathrm{3}}]{\mathrm{17}+\mathrm{3}\sqrt{\mathrm{33}}}}{\mathrm{3}}=\mathrm{0}.\mathrm{543689} \\ $$$$ \\ $$$${sin}\left({x}\right)=\mathrm{0}.\mathrm{543689}\Rightarrow{sin}^{\mathrm{2}} \left({x}\right)=\mathrm{0}.\mathrm{295598} \\ $$$${x}=\mathrm{32}.\mathrm{94}° \\ $$$${cot}^{\mathrm{2}} \left({x}\right)=\mathrm{2}.\mathrm{38209} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com