Question and Answers Forum

All Questions      Topic List

Differentiation Questions

Previous in All Question      Next in All Question      

Previous in Differentiation      Next in Differentiation      

Question Number 129344 by bramlexs22 last updated on 15/Jan/21

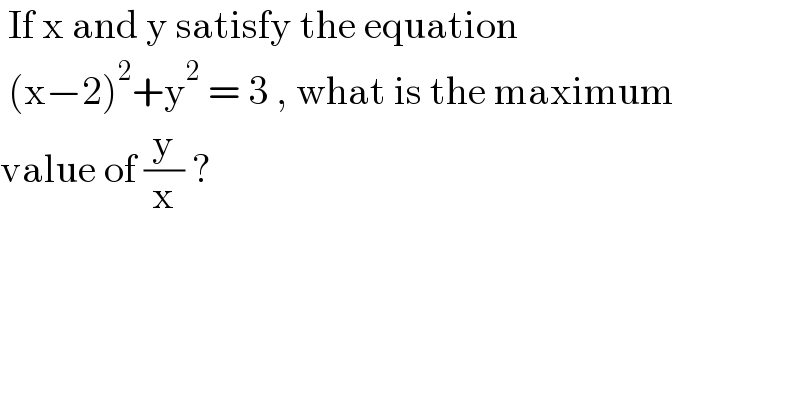
If x and y satisfy the equation (x−2)^2 +y^2 = 3 , what is the maximum value of (y/x) ?

$$\:\mathrm{If}\:\mathrm{x}\:\mathrm{and}\:\mathrm{y}\:\mathrm{satisfy}\:\mathrm{the}\:\mathrm{equation}\: \\ $$$$\:\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \:=\:\mathrm{3}\:,\:\mathrm{what}\:\mathrm{is}\:\mathrm{the}\:\mathrm{maximum} \\ $$$$\mathrm{value}\:\mathrm{of}\:\frac{\mathrm{y}}{\mathrm{x}}\:? \\ $$

Answered by liberty last updated on 15/Jan/21

f(x) = ((±(√(3−(x−2)^2 )))/x) = ((± (√(4x−x^2 −1)))/x) f ′(x)=± [(( x(((2−x)/( (√(4x−x^2 −1)))))−(√(4x−x^2 −1)))/x^2 ) ] =0 ⇒ ± (2x−x^2 −(4x−x^2 −1))=0 ⇒± (1−2x)=0 ⇒x = (1/2) f((1/2)) = ±((√(3−((1/2)−2)^2 ))/(1/2))=±2 (√(3/4)) ((y/x))_(max) = (√3) ; ((y/x))_(min) =−(√3)

$$\:\mathrm{f}\left(\mathrm{x}\right)\:=\:\frac{\pm\sqrt{\mathrm{3}−\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{2}} }}{\mathrm{x}}\:=\:\frac{\pm\:\sqrt{\mathrm{4x}−\mathrm{x}^{\mathrm{2}} −\mathrm{1}}}{\mathrm{x}} \\ $$$$\:\mathrm{f}\:'\left(\mathrm{x}\right)=\pm\:\left[\frac{\:\mathrm{x}\left(\frac{\mathrm{2}−\mathrm{x}}{\:\sqrt{\mathrm{4x}−\mathrm{x}^{\mathrm{2}} −\mathrm{1}}}\right)−\sqrt{\mathrm{4x}−\mathrm{x}^{\mathrm{2}} −\mathrm{1}}}{\mathrm{x}^{\mathrm{2}} }\:\right]\:=\mathrm{0} \\ $$$$\Rightarrow\:\pm\:\left(\mathrm{2x}−\mathrm{x}^{\mathrm{2}} −\left(\mathrm{4x}−\mathrm{x}^{\mathrm{2}} −\mathrm{1}\right)\right)=\mathrm{0} \\ $$$$\Rightarrow\pm\:\left(\mathrm{1}−\mathrm{2x}\right)=\mathrm{0}\:\Rightarrow\mathrm{x}\:=\:\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\:=\:\pm\frac{\sqrt{\mathrm{3}−\left(\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{2}\right)^{\mathrm{2}} }}{\frac{\mathrm{1}}{\mathrm{2}}}=\pm\mathrm{2}\:\sqrt{\frac{\mathrm{3}}{\mathrm{4}}} \\ $$$$\:\left(\frac{\mathrm{y}}{\mathrm{x}}\right)_{\mathrm{max}} =\:\sqrt{\mathrm{3}}\:\:;\:\left(\frac{\mathrm{y}}{\mathrm{x}}\right)_{\mathrm{min}} =−\sqrt{\mathrm{3}}\: \\ $$

Answered by mr W last updated on 15/Jan/21

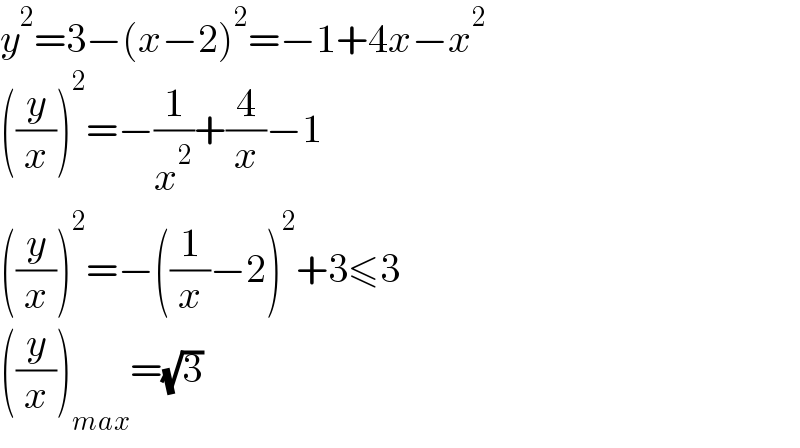
y^2 =3−(x−2)^2 =−1+4x−x^2 ((y/x))^2 =−(1/x^2 )+(4/x)−1 ((y/x))^2 =−((1/x)−2)^2 +3≤3 ((y/x))_(max) =(√3)

$${y}^{\mathrm{2}} =\mathrm{3}−\left({x}−\mathrm{2}\right)^{\mathrm{2}} =−\mathrm{1}+\mathrm{4}{x}−{x}^{\mathrm{2}} \\ $$$$\left(\frac{{y}}{{x}}\right)^{\mathrm{2}} =−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\frac{\mathrm{4}}{{x}}−\mathrm{1} \\ $$$$\left(\frac{{y}}{{x}}\right)^{\mathrm{2}} =−\left(\frac{\mathrm{1}}{{x}}−\mathrm{2}\right)^{\mathrm{2}} +\mathrm{3}\leqslant\mathrm{3} \\ $$$$\left(\frac{{y}}{{x}}\right)_{{max}} =\sqrt{\mathrm{3}} \\ $$

Commented by liberty last updated on 15/Jan/21

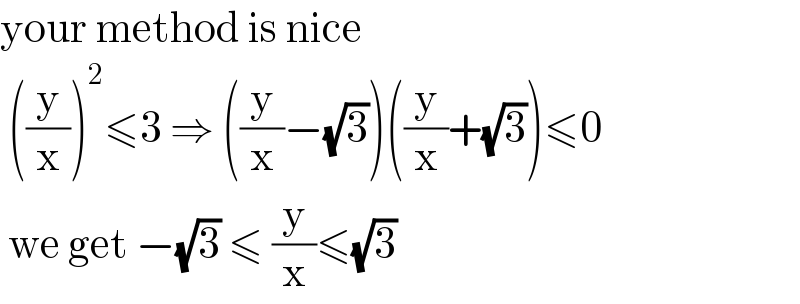
your method is nice ((y/x))^2 ≤3 ⇒ ((y/x)−(√3))((y/x)+(√3))≤0 we get −(√3) ≤ (y/x)≤(√3)

$$\mathrm{your}\:\mathrm{method}\:\mathrm{is}\:\mathrm{nice} \\ $$$$\:\left(\frac{\mathrm{y}}{\mathrm{x}}\right)^{\mathrm{2}} \leqslant\mathrm{3}\:\Rightarrow\:\left(\frac{\mathrm{y}}{\mathrm{x}}−\sqrt{\mathrm{3}}\right)\left(\frac{\mathrm{y}}{\mathrm{x}}+\sqrt{\mathrm{3}}\right)\leqslant\mathrm{0} \\ $$$$\:\mathrm{we}\:\mathrm{get}\:−\sqrt{\mathrm{3}}\:\leqslant\:\frac{\mathrm{y}}{\mathrm{x}}\leqslant\sqrt{\mathrm{3}}\: \\ $$

Commented by mr W last updated on 15/Jan/21

you are fast!

$${you}\:{are}\:{fast}! \\ $$

Commented by liberty last updated on 15/Jan/21

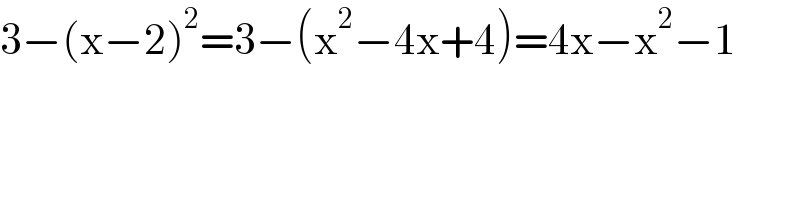
3−(x−2)^2 =3−(x^2 −4x+4)=4x−x^2 −1

$$\mathrm{3}−\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{2}} =\mathrm{3}−\left(\mathrm{x}^{\mathrm{2}} −\mathrm{4x}+\mathrm{4}\right)=\mathrm{4x}−\mathrm{x}^{\mathrm{2}} −\mathrm{1} \\ $$

Commented by bramlexs22 last updated on 15/Jan/21

yes..thanks

$$\mathrm{yes}..\mathrm{thanks} \\ $$

Answered by ajfour last updated on 15/Jan/21

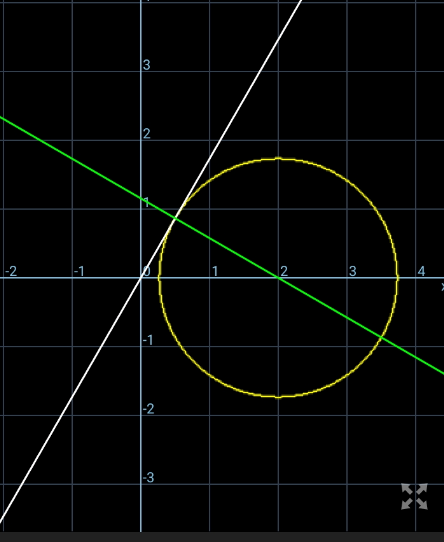
Commented by ajfour last updated on 15/Jan/21

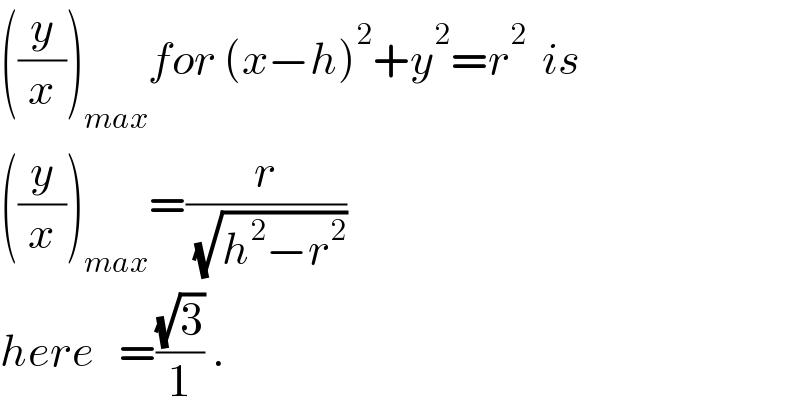
((y/x))_(max) for (x−h)^2 +y^2 =r^2 is ((y/x))_(max) =(r/( (√(h^2 −r^2 )))) here =((√3)/1) .

$$\left(\frac{{y}}{{x}}\right)_{{max}} {for}\:\left({x}−{h}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} ={r}^{\mathrm{2}} \:\:{is} \\ $$$$\left(\frac{{y}}{{x}}\right)_{{max}} =\frac{{r}}{\:\sqrt{{h}^{\mathrm{2}} −{r}^{\mathrm{2}} }}\: \\ $$$${here}\:\:\:=\frac{\sqrt{\mathrm{3}}}{\mathrm{1}}\:. \\ $$

Commented by liberty last updated on 15/Jan/21

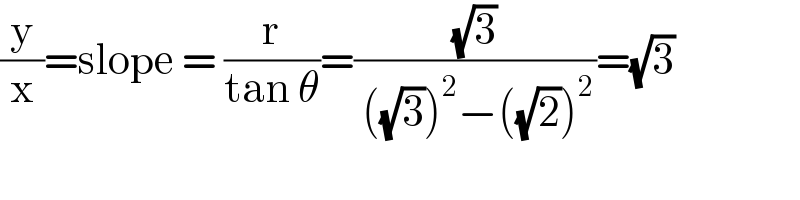
(y/x)=slope = (r/(tan θ))=((√3)/( ((√3))^2 −((√2))^2 ))=(√3)

$$\frac{\mathrm{y}}{\mathrm{x}}=\mathrm{slope}\:=\:\frac{\mathrm{r}}{\mathrm{tan}\:\theta}=\frac{\sqrt{\mathrm{3}}}{\:\left(\sqrt{\mathrm{3}}\right)^{\mathrm{2}} −\left(\sqrt{\mathrm{2}}\right)^{\mathrm{2}} }=\sqrt{\mathrm{3}} \\ $$

Answered by Olaf last updated on 15/Jan/21

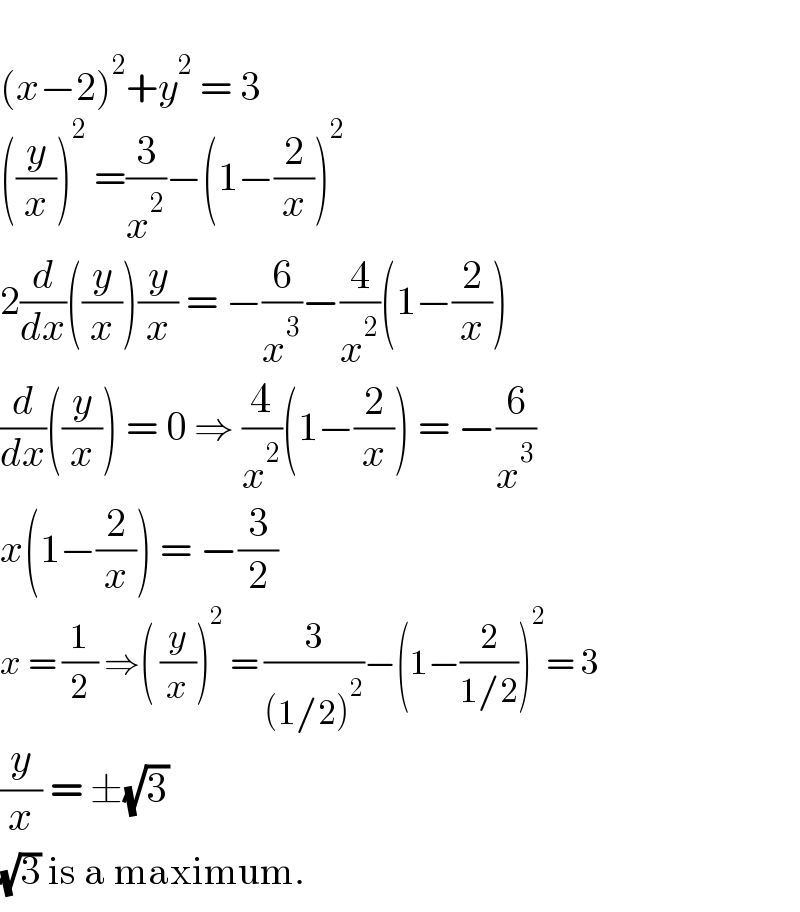
(x−2)^2 +y^2 = 3 ((y/x))^2 =(3/x^2 )−(1−(2/x))^2 2(d/dx)((y/x))(y/x) = −(6/x^3 )−(4/x^2 )(1−(2/x)) (d/dx)((y/x)) = 0 ⇒ (4/x^2 )(1−(2/x)) = −(6/x^3 ) x(1−(2/x)) = −(3/2) x = (1/2) ⇒( (y/x))^2 = (3/((1/2)^2 ))−(1−(2/(1/2)))^2 = 3 (y/x) = ±(√3) (√3) is a maximum.

$$ \\ $$$$\left({x}−\mathrm{2}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} \:=\:\mathrm{3} \\ $$$$\left(\frac{{y}}{{x}}\right)^{\mathrm{2}} \:=\frac{\mathrm{3}}{{x}^{\mathrm{2}} }−\left(\mathrm{1}−\frac{\mathrm{2}}{{x}}\right)^{\mathrm{2}} \\ $$$$\mathrm{2}\frac{{d}}{{dx}}\left(\frac{{y}}{{x}}\right)\frac{{y}}{{x}}\:=\:−\frac{\mathrm{6}}{{x}^{\mathrm{3}} }−\frac{\mathrm{4}}{{x}^{\mathrm{2}} }\left(\mathrm{1}−\frac{\mathrm{2}}{{x}}\right) \\ $$$$\frac{{d}}{{dx}}\left(\frac{{y}}{{x}}\right)\:=\:\mathrm{0}\:\Rightarrow\:\frac{\mathrm{4}}{{x}^{\mathrm{2}} }\left(\mathrm{1}−\frac{\mathrm{2}}{{x}}\right)\:=\:−\frac{\mathrm{6}}{{x}^{\mathrm{3}} } \\ $$$${x}\left(\mathrm{1}−\frac{\mathrm{2}}{{x}}\right)\:=\:−\frac{\mathrm{3}}{\mathrm{2}} \\ $$$${x}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\left(\:\frac{{y}}{{x}}\right)^{\mathrm{2}} \:=\:\frac{\mathrm{3}}{\left(\mathrm{1}/\mathrm{2}\right)^{\mathrm{2}} }−\left(\mathrm{1}−\frac{\mathrm{2}}{\mathrm{1}/\mathrm{2}}\right)^{\mathrm{2}} =\:\mathrm{3} \\ $$$$\frac{{y}}{{x}}\:=\:\pm\sqrt{\mathrm{3}} \\ $$$$\sqrt{\mathrm{3}}\:\mathrm{is}\:\mathrm{a}\:\mathrm{maximum}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com